Skip to main content

The Theory of Statistical Distributions

9 Mixed distributions

On completion of this chapter, you should be able to:

  • recognise mixed random variables.
  • recognise censored models, hurdle models and compound Poisson–gamma models for modelling mixed random variables.
  • know the basic properties of the above mixed distributions.
  • apply these distributions as appropriate to problem solving.

9.1 Introduction

Mixed random variables commonly occur, but are not often studied. Mixed random variables appear in diverse applications such as insurance, agriculture, climatology, fishing, etc.

In most practical cases, a mixed random variable \(X\) has a discrete probability mass at \(X = 0\), and then are continuous for \(X > 0\); this is the only type of mixed random variable we consider (though extensions to discrete masses occurring for other values of the random variable are often (but not always) similar). For example:

  • When modelling insurance, the zero probability corresponds to portfolios with zero claims; however, when claims are made, the total claim amount has a continuous distribution.
  • When modelling rainfall, the zero probability corresponds to receiving zero rainfall; however, when rain does fall, the total rainfall recorded has a continuous distribution.
  • When modelling fish catch, the zero probability corresponds to catching zero fish; however, when fish are caught, the mass of fish catch has a continuous distribution.

Continuous data with a discrete probability at zero can be modelled in various ways, depending on how the discrete probability at \(X = 0\) is incorporated. Three approaches are considered in this chapter.

Censored models (Sect. 9.2) assume the existence of an underlying latent variable, defined for all real values. However, values of the latent variable below zero cannot be observed (called censoring). All the probabilities corresponding to values of the latent variable below zero are accumulated, and assigned to the probability of observing a value of zero. The value of \(X = 0\) represents censored observations of the latent variable.

Hurdle models (Sect. 9.3) treat the zeros as emerging from a two-step process. Step one is a binary process, that models whether the event of interest (i.e., an insurance claim is made; rainfall is recorded; fish are caught) occurs. Step two is a model for the continuous data of interest, conditional on the event of interest occurring.

Compound Poisson-gamma models (Sect. 9.4) combine the discrete and continuous components in a single probability model. Unlike the hurdle model, the discrete and continuous parts are not modelled separately; the entire distribution is modelled using a single probability model specific for modeling mixed random variables.

9.2 Censored model

9.2.1 Definitions

Censored models assume the existence of an unobserved latent variable, say \(Y\), such that \(Y\in\mathbb{R}\) with probability function \(f_Y(y)\). Values of \(Y\) below some threshold, say \(y^*\) (commonly, \(y^* = 0\)), are not directly observed. Instead, \(X = \max(Y^*, Y)\) is observed; that is, values of \(Y\) less than \(y^*\) are recorded as \(y^*\). We will focus on the case where \(y^* = 0\).

Example 9.1 (Latent variables and censoring) Consider a latent variable defined as the ‘desire to purchase alcohol’ \(Y\), where the value \(Y = 0\) represents indifference to purchasing alcohol. Some people may have a very strong aversion to purchasing alcohol, so that the value of \(Y\) is large and negative. Some people may have a mild aversion to purchasing alcohol, so that the value of \(Y\) is small but still negative. In both cases, however, an aversion to purchasing alcohol is present, and no alcohol is purchased.

The observed variable of interest could be \(X\), the average weekly spend on buying alcohol in dollars. When \(Y \le 0\), we observe \(X = 0\); however, when \(Y > 0\), a continuous amount is spent on purchasing alcohol (Fig. 9.1).

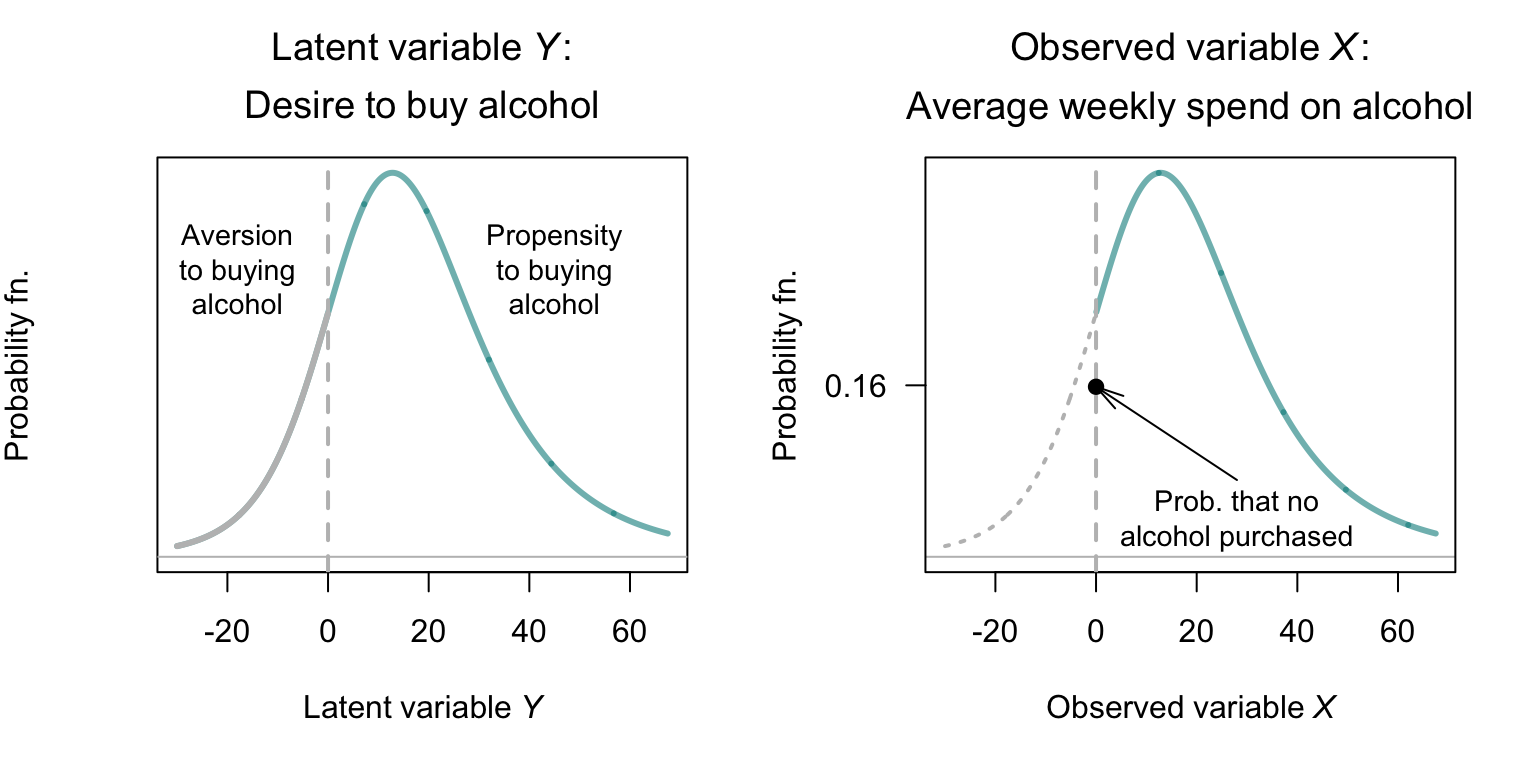
Left: the latent variable\ $Y$, the desire to buy alcohol. Right: the observed variable\ $X$, the average weekly spend on alcohol. The solid dot is the sum of all probabilities for which $Z \le 0$.

FIGURE 9.1: Left: the latent variable \(Y\), the desire to buy alcohol. Right: the observed variable \(X\), the average weekly spend on alcohol. The solid dot is the sum of all probabilities for which \(Z \le 0\).

In this context, the value of the observed variable \(X\) is said to be censored.

Definition 9.1 (Censoring) A variable is called censored if its value is only observed when its above or below a certain threshold.

Left censoring occurs when the true (latent) value is less than or equal to a known threshold, but the exact value is unknown. We only know that the true (latent) value is below a certain threshold.

Right censoring occurs when the true (latent) value is greater than or equal to a known threshold, but the exact value is unknown. We only know that the true (latent) value is above a certain threshold.

Example 9.2 (Left censoring) The latent variable ‘desire to purchase alcohol’ used in Example 9.1 is left censored.

Example 9.3 In survival analysis, the time it takes insects to die (say \(X\)) may be studied. If the study ends at time \(t^*\), the time of death for any insects still alive is some value larger than \(t^*\); that is, \(X\ge t^*\) but the exact time of death remains unknown. The time to death is right censored.

Censoring is not the same as truncation.

Censoring retains observations, but the exact value remains unknown. Truncation removes observations whose value falls above or below a threshold.

Usually \(y^* = 0\) (as in Example 9.1), so that any value of \(Y \le 0\) is recorded as \(y = 0\). That is, we observe the random variable \(X\) such that \[ X = \max(Y, 0). \] This means the probability function of \(X\) is \[ f_X(x) = \begin{cases} 0 & \text{if $X < 0$}\\ F_Y(0) & \text{if $X = 0$}\\ f_Y(y) & \text{if $X > 0$} \end{cases} \] where \(F_Y(y)\) is the distribution function of \(Y\). The probability function for \(X\mid X > 0\), the continuous part of the distribution only, is \[\begin{equation} f_{X\mid X > 0}(x) = \frac{f_X(x)}{\Pr(X > 0)} = \frac{f_Y(y)}{1 - F_Y(0)} \tag{9.1} \end{equation}\] where again \(F_Y(y)\) is the distribution function of \(Y\). The distribution function of \(X\) is \[ F_{X\mid X>0}(x) = \begin{cases} 0 & \text{for $x < 0$}\\ F_Y(0) & \text{for $x = 0$}\\ F_Y(x) & \text{for $x > 0$} \end{cases} \]

If the latent distribution is a normal distribution, Equation (9.1) can be written in terms of the standard normal density function \(\phi(\cdot)\) and the standard normal distribution function \(\Phi(\cdot)\) (see Sect. 8.3.2). In this case only, notice that \[\begin{align*} \Pr(X > 0) &= \Pr(Z > (0 - \mu)/\sigma)\quad\text{(where $Z$ is a standard normal variate)} \\ &= \Pr(Z > -\mu/\sigma) \\ &= 1 - \Phi( -\mu/\sigma) \\ &= \Phi(\mu/\sigma) \quad\text{(using the symmetry of the normal distribution)}, \end{align*}\] and hence Equation (9.1) can be written as \[\begin{equation} f_{X\mid X>0}(x) = \frac{\phi\big((x-\mu)/\sigma\big)}{\Phi(\mu/\sigma)}. \tag{9.2} \end{equation}\] If we write \(t = \mu/\sigma\) and define \(\lambda(t) = \phi(t)/\Phi(t)\), this expression becomes \[ f_{X\mid X>0}(x) = ????????????? \] LOST: \[ f_{X\mid X>0}(x) = \frac{f_Z(x)}{\Pr(Z > 0)} = \frac{f_Z(x)}{1 - F_Z(0)} \]

Example 9.4 (Latent variables and censoring) Consider the number of hours worked (which can be observed), which must take a non-negative value. We could assume an underlying, unobserved latent variable such as ‘willingness to work’. Negative values for ‘willingness to work’, no matter how small or how large, all result in zero observed hours of work.

9.2.2 Properties

The expected value of the censored random variable \(X\) can be found first separating the discrete and continuous parts of the distribution: \[\begin{align*} \operatorname{E}[X] &= \operatorname{E}[X\mid X = 0] + \operatorname{E}[X\mid X > 0]\\ &= \Pr(X = 0)\times 0 + \operatorname{E}[X\mid X > 0]\\ &= \operatorname{E}[X\mid X > 0]\\ &= \int_0^\infty x\cdot f_{X\mid X > 0}(x)\,dx,\\ &= \frac{1}{\Phi()} \int_0^\infty x\cdot f_{X}(x)\,dx, \end{align*}\] where \(f_{X\mid X > 0}(x)\) is given in Equation (9.2)).

When the censoring happens at \(x^* = 0\), the standardised score is \((x^* - \mu)/\sigma = -t\), where defining \(t = \mu/\sigma\) proves useful. Then \(1 - \Phi()\) Thus, \[\begin{align*} \operatorname{E}[X] &= \int_0^\infty x\cdot f_{X\mid X > 0}(x)\,dx, &= \int_0^\infty x\cdot f_{X\mid X > 0}(x)\,dx, \end{align*}\]

Similarly, \[ \operatorname{E}[X^2] = \operatorname{E}[X^2 \mid X > 0] = \int_0^\infty x^2 \cdot f_{X\mid X>0}(x)\, dx, \] from which the variance can be obtained. The same approach also gives the MGF as \[ M_X(t) = M_{X\mid X > 0}(t). \] Clearly, further progress with these expressions requires knowing the distribution of \(X\) and hence the distribution of the latent variable \(Z\). It is common, but by no means universal, for the latent variable to be described by a normal distribution (when the models are also called Tobit models).

Example 9.5 (Censored model) Consider a latent variable \(Y\), and an observed variable \(X = \text{max}(0, Z)\). Suppose that \(Z\) has the normal distribution (Fig. 9.2, left panel)) \[ Z \sim N(\mu = 0, \sigma^2 = 1), \] so that \(\operatorname{E}[Z] = 0\) and \(\operatorname{var}[Z] = 1\). That is, \(Z\) has a standard normal distribution (Sect 8.3.2), and so \[ \Pr(Z < 0) = \Phi(0) = 0.5. \] Recall the notation: \(\Phi(\cdot)\) is the distribution function for a standard normal variate, and \(\phi(\cdot)\) is the density function for a standard normal variate.

Then, define the random variable \(X\) as \[ f_X(x) = \begin{cases} 0 & \text{if $Z < 0$};\\ \Phi(0) & \text{if $Z = 0$};\\ \phi(x) & \text{if $Z > 0$}, \end{cases} \] as shown in Fig. 9.2 (right panel).

From Equation (9.1), \[ f_{X\mid X > 0}(x) = \frac{\phi(x)}{1 - \Phi(0)} = 2 \phi(x) \] for \(X > 0\). From this expression, \[ \operatorname{E}[X] = \operatorname{E}[X \mid X > 0] = 2 \int_0^\infty x\cdot \phi(x)\, dx = \frac{2}{\sqrt{2\pi}} \approx 0.7979, \] integrating the expression for \(\phi(x)\) (Equation (8.4)). Similarly, using integration by parts, \[ \operatorname{E}[X^2] = \operatorname{E}[X^2 \mid X > 0] = 2 \int_0^\infty x^2\cdot \phi(x)\, dx = 1/2. \] Combining, this means that \[ \operatorname{var}[X] = \frac{1}{2} - \left(\frac{2}{\sqrt{2\pi}}\right)^2 = \frac{1}{2} - \frac{1}{\pi} \approx 0.182. \]

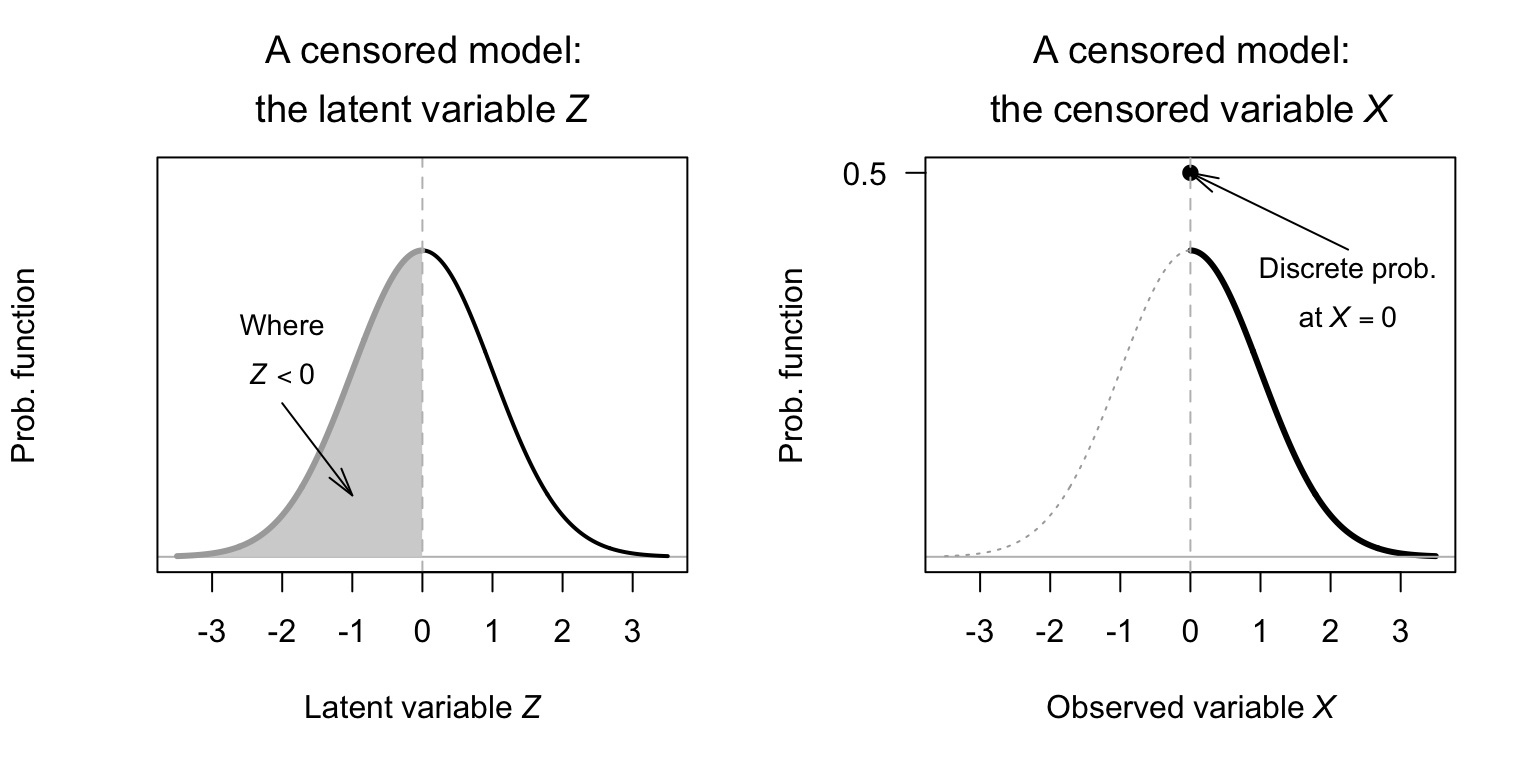
A censored model, using a normal distribution for the continuous component, with the threshold value at $Z = 0$.

FIGURE 9.2: A censored model, using a normal distribution for the continuous component, with the threshold value at \(Z = 0\).

9.3 Hurdle models

9.3.1 Definitions

A hurdle model treats the zero values of the random variable \(X\) as emerging from a two-step process. The first step uses a Bernoulli distribution (Sect. 7.3) to model a random variable \(Y\) that defines whether an event of interest occurs: \[ \Pr(Y) = \begin{cases} 1 - p & \text{if $Y = 0$; i.e., the event of interest \emph{does not} occur;}\\ p & \text{if $Y = 1$; i.e., the event of interest \emph{does} occur.} \end{cases} \] If the event does occur (i.e., conditional on \(X > 0\)), with probability \(1 - p\), then the continuous component is modelled using a probability density function \(f^+_X(x)\) defined for positive real values only (such as an exponential distribution or a gamma distribution).

The probability function for the mixed random variable \(X\) is therefore \[ f_X(x) = \begin{cases} 1 - p & \text{if $x = 0$}\\ p\cdot f^+_X(x) & \text{if $x > 0$,} \end{cases} \] where \(f^+_X(x) = f_{X \mid X > 0}(x)\) is the density function for the continuous distribution defined for \(x\in\mathbb{R}_{+}\). The distribution function is \[ F_X(x) = \begin{cases} 0 & \text{if $x < 0$}\\ 1 - p & \text{if $x = 0$}\\ (1 - p) + p\cdot F^+_X(x) & \text{if $x > 0$,} \end{cases} \] where \(F^+_X(x) = F_{X\mid X > 0}(x)\) is the distribution function for the continuous distribution defined for \(x\in\mathbb{R}_{+}\).

Example 9.6 (Hurdle model) Consider the mixed random variable \(X\), with probability function \(f_X(x)\). Suppose that, when \(X > 0\), an exponential distribution is used to describe the distribution; that is \[ f^+_X(x) = \frac{1}{\lambda}\exp(-x/\lambda)\quad\text{for $x > 0$}. \] Then, using \(p = 0.7\) and \(\lambda = 1/2\), the probability function of \(X\) is \[ f_X(x) = \begin{cases} 0.3 & \text{if $x = 0$}\\ 0.35\cdot \exp(-x/2) & \text{if $x > 0$;} \end{cases} \] see Fig. 9.3.

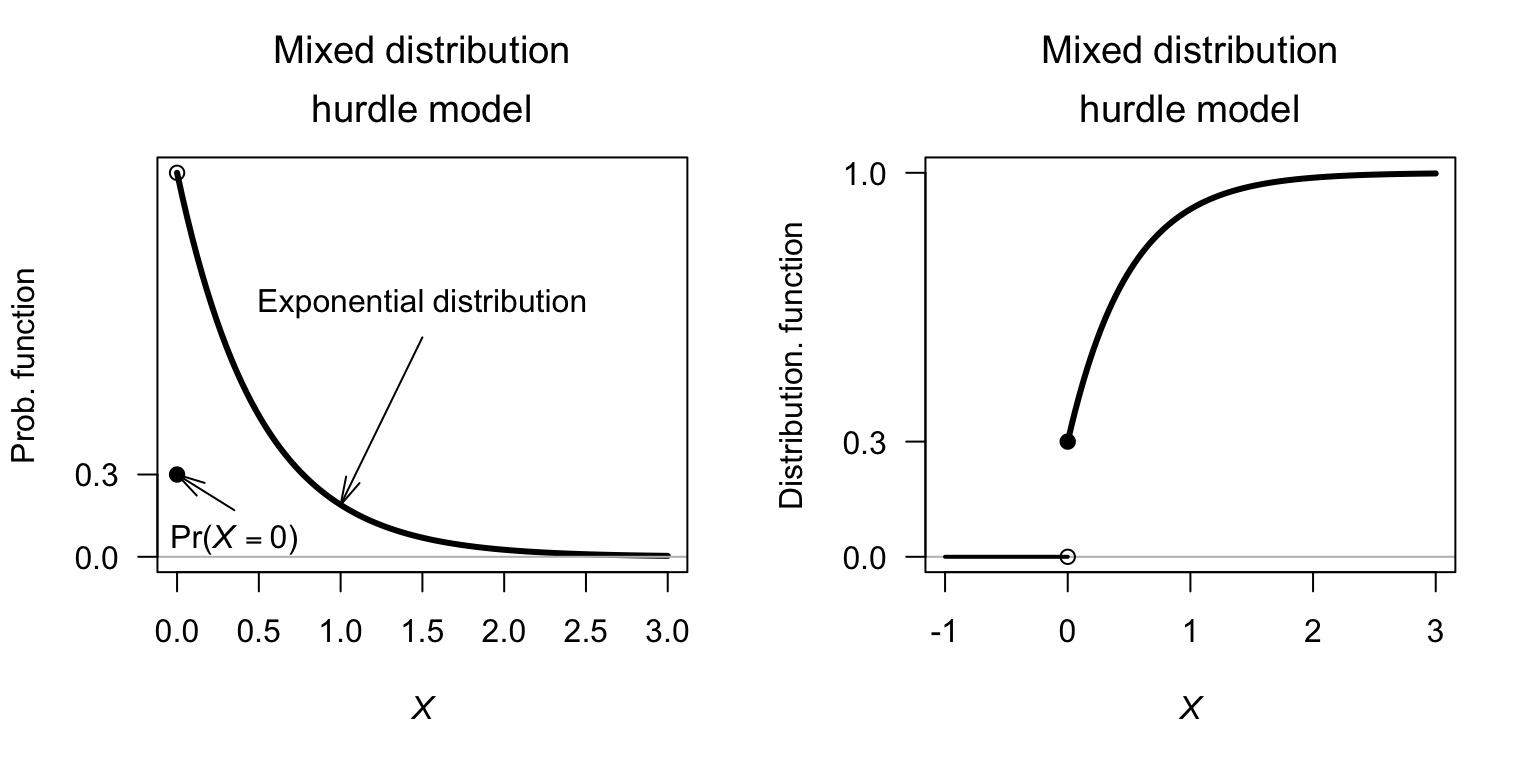
A hurdle model, showing an exponential distribution for the continuous component.

FIGURE 9.3: A hurdle model, showing an exponential distribution for the continuous component.

9.3.2 Properties

The expected value of the random variable \(X\) can be found first separating the discrete and continuous parts of the distribution: \[\begin{align*} \operatorname{E}[X] &= \operatorname{E}[X\mid X = 0] + \operatorname{E}[X\mid X > 0]\\ &= (1 - p)\times 0 + p \operatorname{E}[X\mid X > 0]\\ &= p \mu^+, \end{align*}\] where \(\mu^+\) denotes \(\operatorname{E}[X\mid X > 0]\), the expected value of the distribution defined for \(X > 0\). Similarly, \[ \operatorname{E}[X^2] = \operatorname{E}[X^2 \mid X > 0] = p (\mu^2)^+, \] where \((\mu^2)^+\) denotes \(\operatorname{E}[X^2\mid X > 0]\). Then, the variance of \(X\) is \[\begin{align*} \operatorname{var}[X] &= p[(\mu^2)^+ - p(\mu^+)^2]\\ &= p(\sigma^2)^+ + p(1 - p)(\mu^+)^2. \end{align*}\] where \(\sigma^2 = \operatorname{var}[X \mid X > 0]\) The same approach also gives the MGF as \[\begin{align*} M_X(t) &= (1 - p) + p\cdot M_{X^+}(t)\\ &= (1 - p) + p\cdot M_{X\mid X > 0}(t), \end{align*}\] where \(M_{X^+}(t)\) is the MGF of the distribution defined for \(X > 0\).

Clearly, further progress with these expressions requires knowing the distribution of \(X | X > 0\)

Example 9.7 (Hurdle model, using gamma distribution) Consider a random variable \(X\) such that \(p = 0.75\) (and hence \(\Pr(X = 0) = 1 - p = 0.25\)), and where the distribution when \(X > 0\) follows a gamma distribution (Sect. 8.5) having \(\alpha = 2\) and \(\beta = 1\), with the density function \[ f_X^{+}(x; \alpha, \beta) = f_{X\mid X > 0}(x; \alpha, \beta) = \frac{1}{\Gamma(2)} x \exp(-x) \quad\text{for $x > 0$}. \] For this gamma distribution, using results from Sect. 8.5, \(\mu^+ = \operatorname{E}[X\mid X > 0] = \alpha\beta = 2\) and \(\operatorname{var}[X\mid X > 0] = \alpha\beta^2 = 2\). Then, the probability function for \(X\) is \[ f_{X}(x) = \begin{cases} 0.25 & \text{for $x = 0$}\\ 0.75 \times f_X^{+}(x; \alpha, \beta) & \text{for $x > 0$.} \end{cases} \] Then \[\begin{align*} \operatorname{E}[X] &= p\cdot \mu^+ = 0.75 \times 2 = 1.5\\ \operatorname{var}[X] &= p(\sigma^2)^+ + p(1 - p)(\mu^+)^2 = 0.75\times 2 + 0.75\times 0.25\times 1.5^2 \approx 1.921. \end{align*}\]

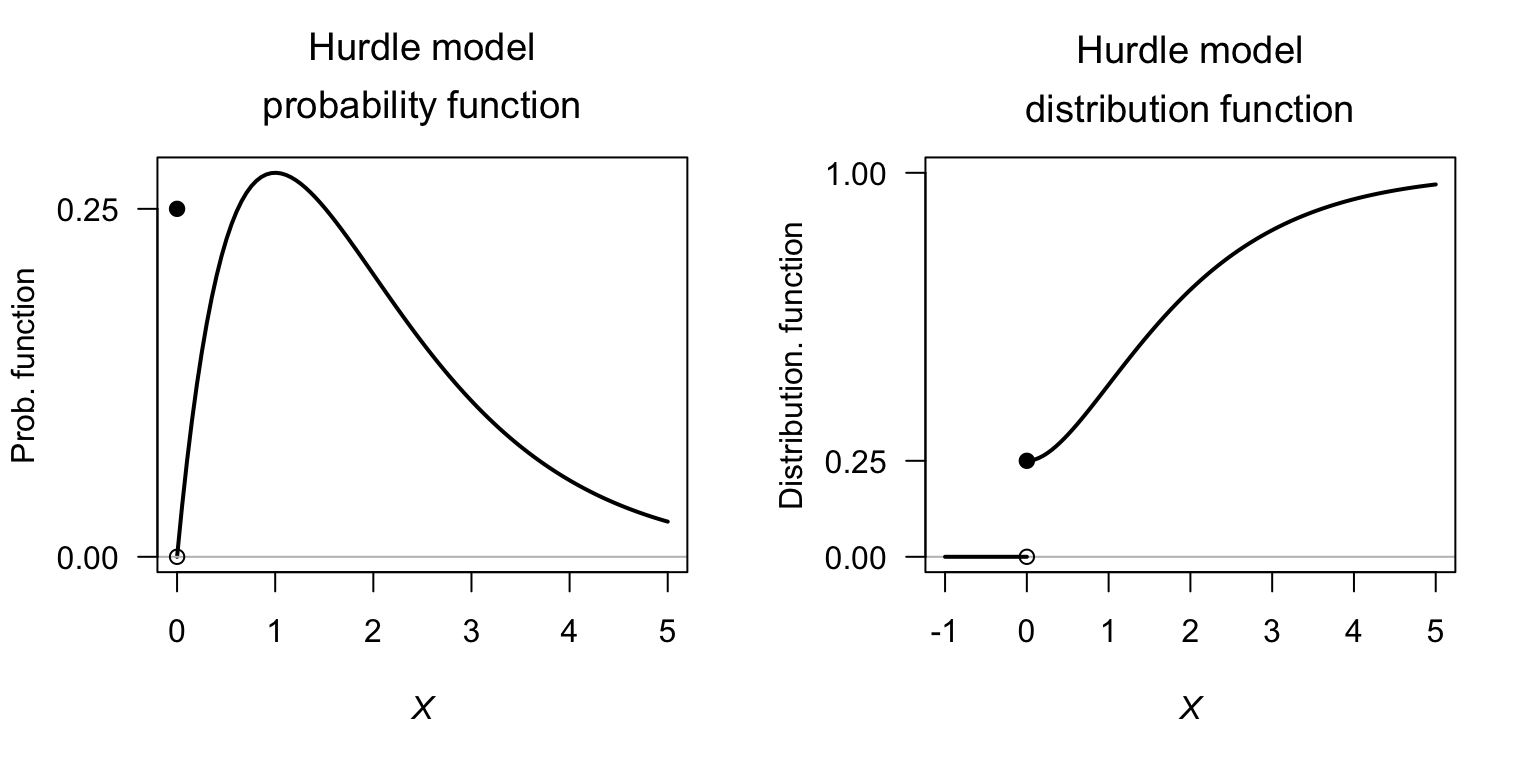
A hurdle model, using a gamma distribution for the continuous component.

FIGURE 9.4: A hurdle model, using a gamma distribution for the continuous component.

9.4 Compound Poisson-gamma distributions

Compound Poisson–gamma distribution take a different approach to modelling mixed random variables: Compound Poisson–gamma distributions model mixed random variables as a Poisson sum of independent gamma distributions. Suppose the number of events observed (which is discrete) is \(N\), such that \[\begin{equation} N \sim \text{Pois}(\lambda). \tag{9.3} \end{equation}\] That is, an event occurs \(N\) times, but occurs at random following a Poisson distribution. Given that \(N\) has a Poisson distribution, it follows (from Sect. 7.7) that \[ \Pr(N = 0) = \exp(-\lambda) \] is the probability that zero events are observed (i.e., \(N = 0\)). If, however, \(N > 0\), then for \(i = 1, 2, \dots, N\), a continuous random variable \(Y_i\) is observed, such that \[ Y_i \sim \text{Gam}(\alpha_i, \beta). \] If \(N = 0\), then no events \(Y_i\) are observed at all; however, if \(N > 0\) then \(N\) events are observed and \[ X = \sum_{i = 1}^N Y_i \] has a continuous distribution. Then, \[ X = \begin{cases} 0 & \text{if $N = 0$};\\ \sum_{i = 1}^N Y_i & \text{if $N > 0$}. \end{cases} \] By this definition \(X\) has a compound Poisson-gamma distribution. The distribution of \(X\) has a probability mass at \(X = 0\) where \(\Pr(Y = 0) = \Pr(N = 0) = \exp(-\lambda)\).

The probability functions for the compound Poisson-gamma distribution cannot be written in closed form. However, the probability function can be expressed as an infinite sum (Dunn and Smyth 2005) or by inverting the MGF (Dunn and Smyth 2008) as discussed in Sect. 5.5.5.

The probability function as an infinite series can be determined from the development of the compound Poisson-gamma distribution above. If \(N = 1\) with \(\Pr(N = 1)\) (from the Poisson distribution), then, \(X = Y\) has the \(\text{Gam}(\alpha, \beta)\) distribution. That is, \[ f_{X\mid N = 1}(x) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} x^{\alpha -1}\exp(-\beta x) \quad \text{for $x > 0$}. \]

If \(N = 2\) with \(\Pr(N = 2)\) (from the Poisson distribution), then, \(X = Y_1 + Y_2\), where \(Y_i \sim\text{Gam}(\alpha, \beta)\) for \(i = 1, 2\). This means that \(X \sim \text{Gam}(2\alpha, \beta)\), which is easily shown using MGFS. (WHY; CROSS REF). That is, \[ f_{X\mid N = 2} (x) = \frac{\beta^{2\alpha}}{\Gamma(2\alpha)} x^{2\alpha -1}\exp(-\beta x) \quad \text{for $x > 0$}. \]

More generally, if \(N = n\) with \(\Pr(N = n)\) (from the Poisson distribution), then, \(X = Y_1 + Y_2+\cdots + Y_n\), and so \(X \sim\text{Gam}(n\alpha, \beta)\), so that \[ f_{X\mid N = n} (x) = \frac{\beta^{n\alpha}}{\Gamma(n\alpha)} x^{n\alpha -1}\exp(-\beta x) \quad \text{for $x > 0$}. \]

Then, using the Law of total probability (Theorem 2.4), \[\begin{align*} f_X(x) &= \sum_{n = 1}^\infty \Pr(N = n) \cdot F_{X\mid N = n}(x)\\ &= \sum_{n = 1}^\infty \frac{\exp(-\lambda)\lambda^n}{n!} \cdot \frac{\beta^{n\alpha}}{\Gamma(n\alpha)} x^{n\alpha -1}\exp(-\beta x)\\ &= \exp(-\lambda - \beta x) \sum_{n = 1}^\infty \frac{\lambda^n}{n!} \frac{\beta^{n\alpha}}{\Gamma(n\alpha)} x^{n\alpha - 1} \end{align*}\] for \(x > 0\). In addition, of course, we have that \[ \Pr(X = 0) = \exp(-\lambda). \]

Even though the probability function has no closed form, the MGF is reasonably simple. To find the MGF, first consider the value of \(N\) as fixed; then, \(X = Y_1 + Y_2 + \cdots + Y_N\) the MGF of \(X\) is \[ M_{X\mid N}(t) = \operatorname{E}[\exp(tX)\mid N]. \] Since the MGF of a sum of independent random variables is the product of their MGFs (Theorem 5.6), we can assume that \(N\) takes some specific value \(n\) and write \[\begin{align*} M_{X\mid N}(t) &= \operatorname{E}\left[ \exp\big(t(Y_2 + Y_2 + \cdots + Y_n)\big)\right] \\ &= \prod_{i = 1}^n \operatorname{E}[\exp(t Y_i)] \\ &= \left( M_Y(t)\right)^n \end{align*}\] So the MGF of \(X\) (rather than \(X\mid N\) as above) is \[\begin{align*} M_X(t) &= \operatorname{E}\left[ \operatorname{E}[ \exp(tX\mid N)]\right] \\ &= \operatorname{E}\left[ M_{X\mid N}(t))\right] \\ &= \operatorname{E}\left[ M_Y(t))^N\right] \\ \end{align*}\] and so \[ M_X(t)=\exp\!\left\{\lambda\left[\Big(\frac{\beta}{\beta-t}\Big)^{\!\alpha}-1\right]\right\},\qquad t<\beta \]

We have \[ M_X(t) = \mathbb{E}[e^{tX}] = \mathbb{E}\!\left[ \big(M_Y(t)\big)^{N} \right]. \] Writing the expectation as a sum over the possible values of \(N\), \[ M_X(t) = \sum_{n=0}^\infty \big(M_Y(t)\big)^{n} \, \Pr(N = n). \] Since \(N \sim \mathrm{Pois}(\lambda)\), \[ \Pr(N = n) = \frac{\exp(-\lambda) \lambda^n}{n!}. \] Substituting this expression into XREF \[\begin{align*} M_X(t) &= \sum_{n = 0}^\infty \big(M_Y(t)\big)^{n} \cdot \frac{\exp(-\lambda) \lambda^n}{n!}\\ &= \exp(-\lambda) \sum_{n = 0}^\infty \frac{\left[\lambda \, M_Y(t)\right]^n}{n!}. \end{align*}\] Using the series expansion \(\sum_{n = 0}^\infty z^n/n! = \exp(z)\) (from Equation (B.8)) with \(z = \lambda M_Y(t)\), this gives \[\begin{align*} M_X(t) &= \exp(-\lambda) \cdot \exp\big(\lambda M_Y(t)\big)\\ &= \exp\{\lambda(M_Y(t) - 1) \\ &= \exp\!\left\{\lambda\left[\Big(\frac{\beta}{\beta-t}\Big)^{\!\alpha}-1\right]\right\}, \end{align*}\] provided \(t < \beta\).

From the MGF we can deduce \[\begin{align*} \operatorname{E}[X] &= \lambda\alpha\/\beta\\ \operatorname{var}[X] &= \lambda\alpha(\alpha + 1)\beta^2. \end{align*}\]

Example 9.8 (Poisson--gamma distribution) Suppose \[ N\sim\text{Pois}(\lambda = 3) \quad\text{and}\quad Y_i \sim\text{Gam}(\alpha = 1/2, \beta = 2/3) \] (where \(\beta\) is the scale parameter). The mean and variance of \(X\) is \[\begin{align*} \operatorname{E}[X] &= \lambda\alpha\/\beta = 3\times \frac{1}{2}\times\frac{2}{3} = 1;\\ \operatorname{var}[X] &= \lambda\alpha(\alpha + 1)\beta^2 = 3\times \left(\frac{1}{2}\times \frac{3}{2}\right)\left(\frac{5}{3}\right)^2 = 1. \end{align*}\] Furthermore, from Equation (9.3), \[ \Pr(X = 0) = \exp(-\lambda) = 0.0498. \] This Poisson-gamma distribution is shown in Fig. 9.5 (right panel).

#> alpha, beta, lambda, p0
#> 20 0.04761905 1.05 0.3499377
#> 0.5 0.6666667 3 0.04978707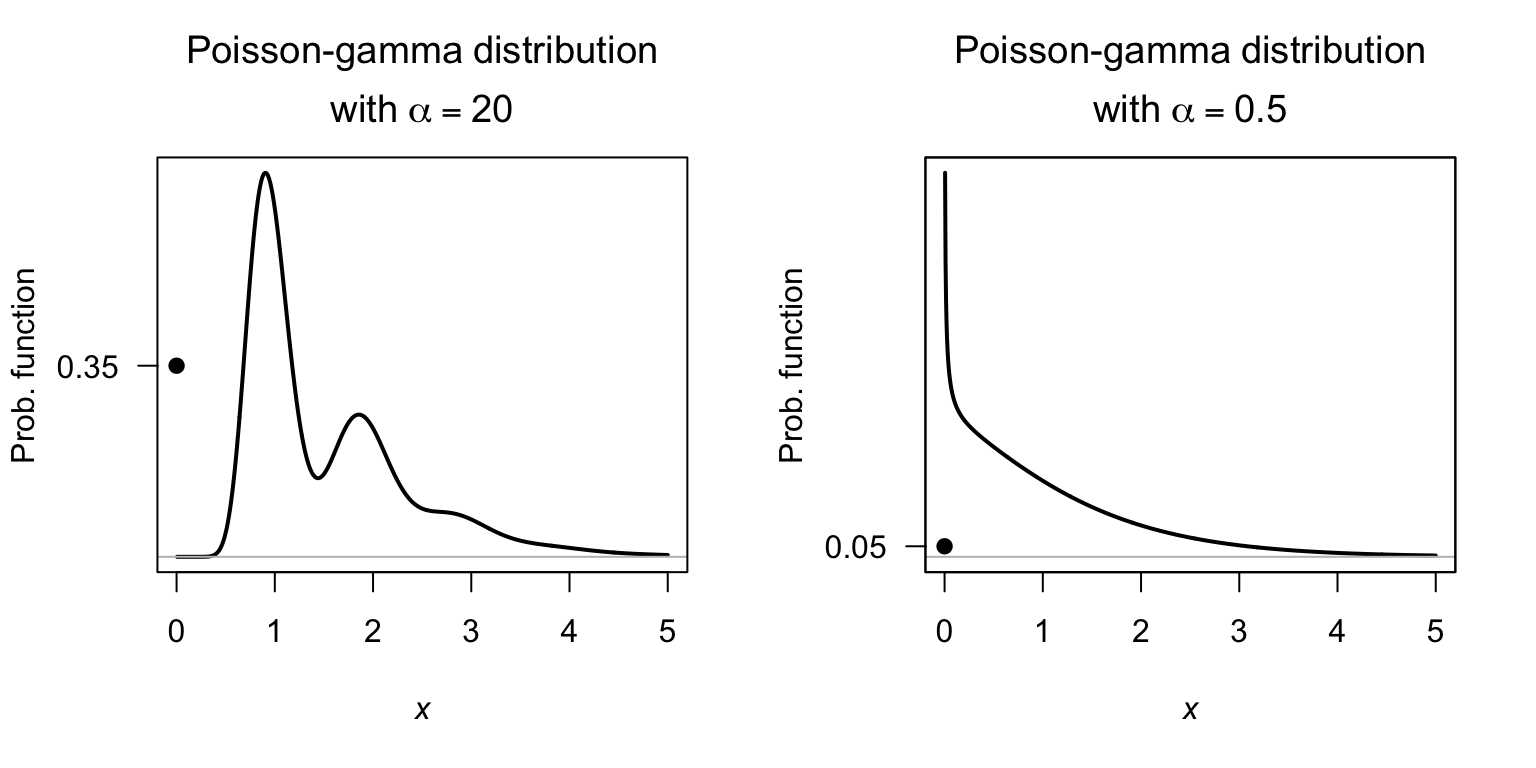
Two compound Poisson--gamma models, both with mean and varaince set to $1$. The solid dot at $X = 0$ represents the discrete probability.

FIGURE 9.5: Two compound Poisson–gamma models, both with mean and varaince set to \(1\). The solid dot at \(X = 0\) represents the discrete probability.

Example 9.9 (Modelling monthly rainfall) Modelling rainfall. Using hurdle from Stern and Coe, Chandler and Wheater? Tobit thing from IWSM, and Poisson–gamma,

9.5 Simulation

9.5.1 General

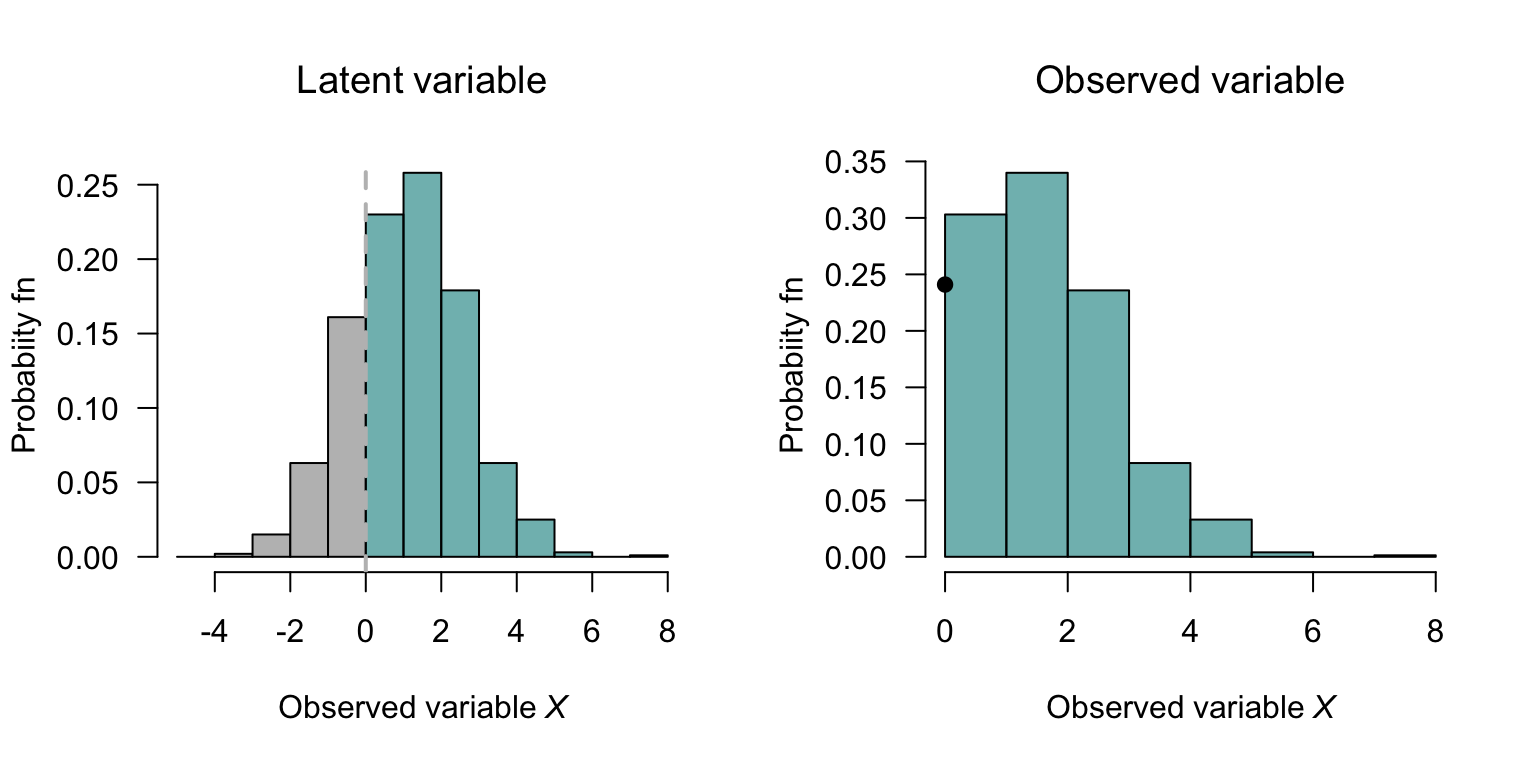
FIX!!!!! The solid dot at $X = 0$ represents the discrete probability.

FIGURE 9.6: FIX!!!!! The solid dot at \(X = 0\) represents the discrete probability.

…

A hurdle model could be used to model daily rainfall (e.g., Stern and Coe (1984)), using a Bernoulli distribution to distinguish wet and dry days, and then a gamma distribution to model rainfall amounts on wet days.

…

A compound Poisson–gamma model could also be used to model daily rainfall (e.g., Yunus et al. (2017)).

Example 9.10 (Simulations for censored models) Censored:

Example 9.11 (Simulations for hurdle models) Hurdle model; see Fig. 9.7

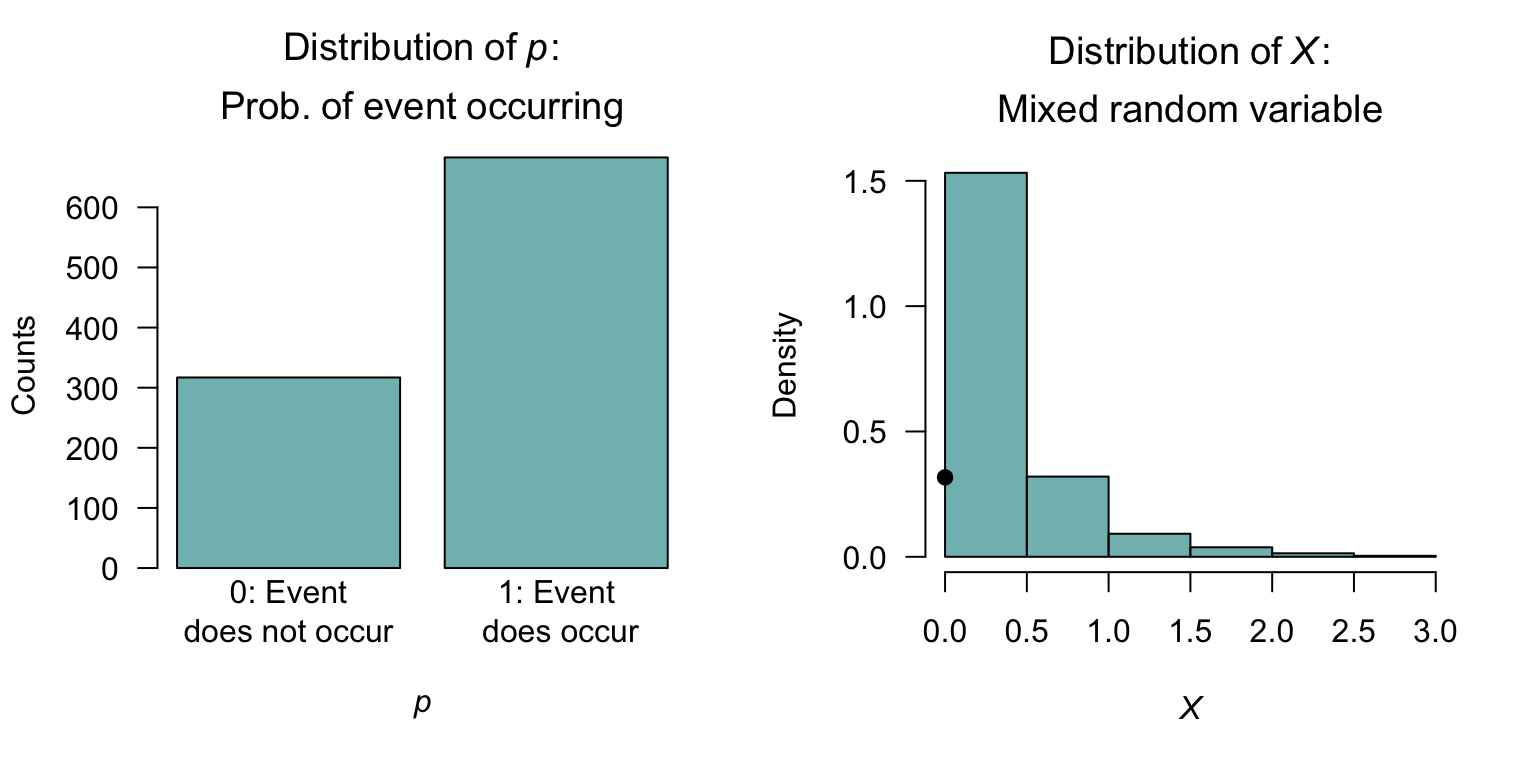
A simulation of the hurdle model. FIX!!!!! The solid dot at $X = 0$ represents the discrete probability.

FIGURE 9.7: A simulation of the hurdle model. FIX!!!!! The solid dot at \(X = 0\) represents the discrete probability.

Example 9.12 (Simulations for compound Poisson--gamma models) Compound P–G; see Fig. 9.8

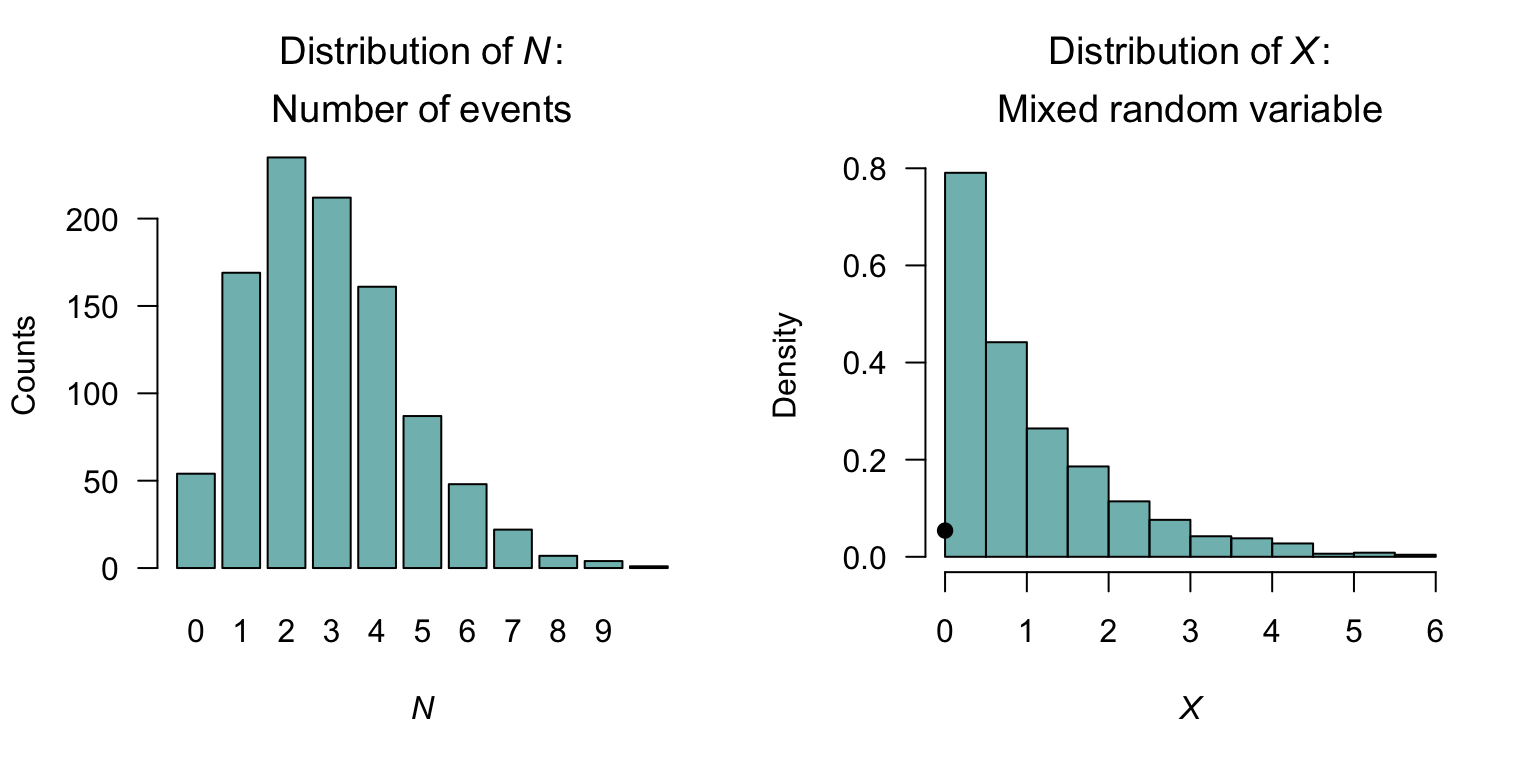
A simulation of the compound Poisson--gamma models, both with mean and variance set to $1$. The solid dot at $X = 0$ represents the discrete probability.

FIGURE 9.8: A simulation of the compound Poisson–gamma models, both with mean and variance set to \(1\). The solid dot at \(X = 0\) represents the discrete probability.

9.5.2 Rainfall

Simulation for the censored, hurdle and compound Poisson-gamma models can all be achieved by directly modelling the process by which the zeros are incorporated. To demonstrate, consider modelling monthly rainfall at a certain location for one specific month each year. Monthly rainfall is a mixed random variable; some months will record exactly zero rainfall, while months in which rain falls will have a continuous rainfall amount recorded.

Simulating monthly rainfall has uses in agriculture, hydrology, forestry and elsewhere (often as an input to other models). The distribution of monthly rainfall obviously varies depending on location and the month selected for modelling; however, monthly rainfall at many locations typically contain some months (historically) that record zero rainfall (see, for example, Hasan and Dunn (2010a)).

Suppose we seek to model the monthly rainfall (im mm) \(R\) at given location for a certain month, where about \(30\)% of months record zero rainfall (i.e., \(\Pr(X = 0) = 0.30\)), and the mean monthly rainfall (when rain is recorded) is about \(\mu_R = 50\).

We could model the monthly rainfall using a censored model (e.g., Sansó and Guenni (2000)), a hurdle model (e.g, Kenabatho et al. (2012)) or a Poisson-gamma distribution (e.g., Hasan and Dunn (2010a)).

First consider a censored model. The latent variable could represent how favourable the conditions are for rainfall’ say \(Y\sim N(\mu_R = 50, \sigma_R^2)\), with \(\Phi(0) = \Pr(Y < 0) = 0.30\), for some variance \(\sigma_R^2\). First, we can find the value of the standard normal variate \(Z\) such that \(\Phi(z) = 0.30 = \Pr(Y < 0)\):

p_Zero_Rainfall <- 0.30
qnorm(p_Zero_Rainfall) # This find z such that Phi(z) = 0.30
#> [1] -0.5244005

This value of \(z\) is the value such that \[ z = -0.5244 = \frac{x^* - \mu_R}{\sigma^2_R} = \frac{0 - 50}{\sigma_R^2}, \] from which we find \(\sigma_R = 95.35\). Thus, the monthly rainfall can be simulated:

set.seed(76103) # For reproducibility
num_Sims <- 1000

mean_R <- 50
sd_R <- -mean_R / qnorm(p0) 

Y <- rnorm(num_Sims,
           mean = mean_R,
           sd = sd_R)
p0 <- 0.30

# To get sd_R, note: z = (0 - mu)/sigma = \Phi(p0) => -mu/sigma = qnorm(p0)
threshold_R <- mean_R  - qnorm(p0) * sd_R # SHOULD BE AT ZERO

###

par(mfrow = c(1, 2))
latent_Breaks <- seq(-250, 450,
                     by = 50)
###  truehist  is part of the MASS package,which must be loaded first, using: 
###  library(MASS)
MASS::truehist(Y,
         las = 1,
         breaks = latent_Breaks,
         col = c( rep( "grey", length(latent_Breaks[latent_Breaks < 0])),
                  rep(plotColour1, length(latent_Breaks[latent_Breaks >= 0])) ),  
         main = expression(Latent~variable),
         ylab = "Probabiity fn",
         xlab = expression(Observed~variable~italic(X)) )

abline(v = 0,
       lwd = 2,
       col = "grey",
       lty = 2)

truehist(Y[Y>0],
         las = 1,
         breaks = latent_Breaks[latent_Breaks>=0],
         main = expression(Observed~variable),
         ylab = "Probabiity fn",
         xlab = expression(Observed~variable~italic(X)) )
points(x = 0,
       y = p0,
       pch = 19)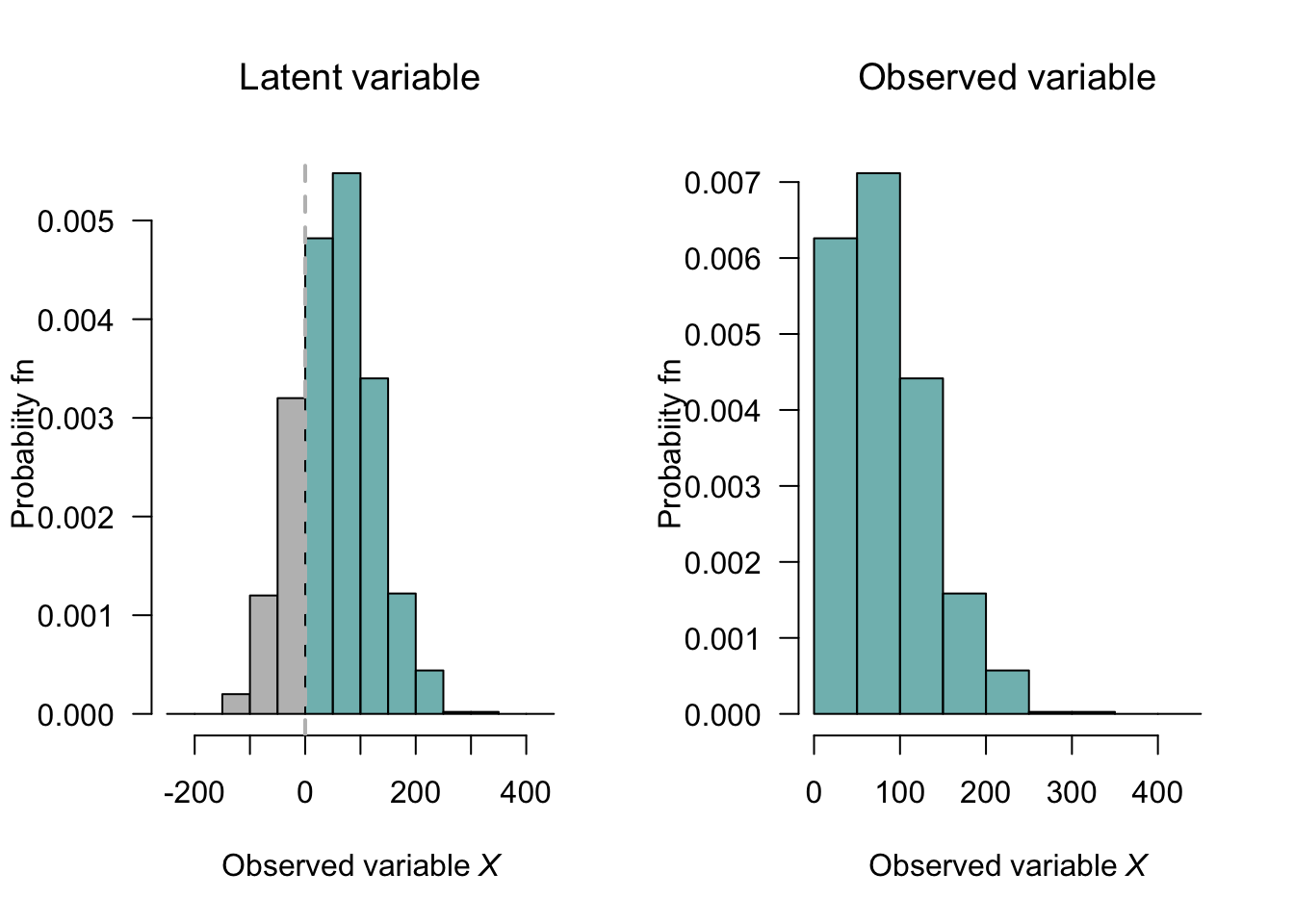
num_Sims <- 1000

#Simulate

# Compute max monthly rainfall

HURDLE:

To model the rainfall using a hurdle model, we use \(1 - p = 0.3\) for the probability that no monthly rainfall is recorded; that is, \(p = 0.7\). The information also gives \(\mu = \operatorname{E} = 50\); from Sect. 9.3.2 \[ \mu = p \mu^+, \] and so \(\mu^+ = \mu/p = 50/0.7 approx 71.43\) is the mean rainfall, conditional on rain being recorded. We could suppose an exponential distribution (with rate parameter \(\lambda\)) for the rainfall amounts when rain is recorded; thus \(\operatorname{E}[X] = 1\lambda = 71.43\) and so \(\lambda = 0.01399972\). So the hurdle model is: \[\begin{align*} f_R(r) &= \begin{cases} 0.3 & \\ 0.3\lambda \exp(-r/\lambda) \end{cases}\\ &= \begin{cases} 0.3 & \\ 0.004199916 \exp(-r/0.01399972). \end{cases} \end{align*}\]

set.seed(76103) # For reproducibility
num_Sims <- 1000

p0 <- 0.30
p <- 1 - p0

mean_R <- 50
mean_Rpositive <- mean_R/p
lambda_Exp <- 1 / mean_Rpositive
  
R <- matrix( NA, ncol = 1, nrow = num_Sims)
p_Each_Month <- rbinom(num_Sims,
                       size = 1,
                       prob = p)

for (i in 1:num_Sims){
  if ((p_Each_Month[i]) == 0){
    R[i] <- 0 # No rainfall recorded
  }  else {
    R[i] <- rexp(1, rate = lambda_Exp)    
  }
}



###
###  truehist  is part of the MASS package,which must be loaded first, using: 
###  library(MASS)
truehist(R,
         las = 1,
         main = expression(Hurdle~model),
         ylab = "Probabiity fn",
         xlab = expression(Observed~rainfall~italic(R)) )

points(x = 0,
       y = p0,
       pch = 19)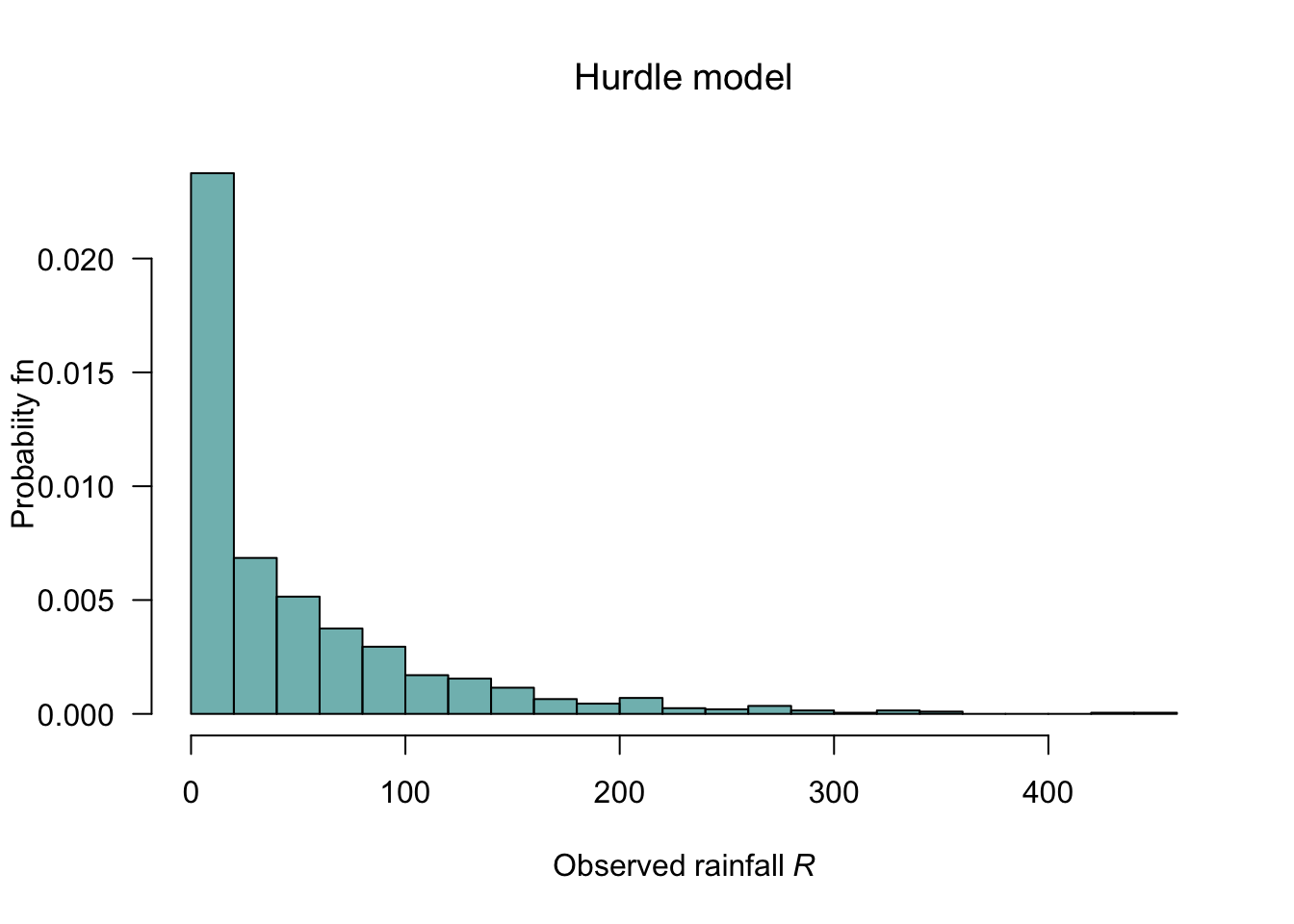
HURDLE MODEL

FIGURE 9.9: HURDLE MODEL

GAMMA SEEMS TO FAIL WITH THESE PARAMETERS ANYWAY: but check

If we use the variance from the censored model (i.e., \(\sigma^2 = 95.35\)), we can find the variance of the gamma distribution: \[\begin{align*} \operatorname{var}[X] &= p(\sigma^2)^+ + p(1 - p)(\mu^+)^2\\ 95.35 &= 0.7(\sigma^2)^+ + 0.7\times 0.3(71.43)^2; \end{align*}\] solving shows that we should use \((\sigma^2)^ = ??\) for the variance of the gamma distribution (when \(X > 0\)).

We could suppose a gamma distribution for the rainfall amounts when rain is recorded; thus \(\alpha\beta = 71.43\). If we use the variance from the censored model (i.e., \(\sigma^2 = 95.35\)), we can find the variance of the gamma distribution: \[\begin{align*} \operatorname{var}[X] &= p(\sigma^2)^+ + p(1 - p)(\mu^+)^2\\ 95.35 &= 0.7(\sigma^2)^+ + 0.7\times 0.3(71.43)^2; \end{align*}\] solving shows that we should use \((\sigma^2)^ = ??\) for the variance of the gamma distribution (when \(X > 0\)).

( 95.35 - 0.7*0.3*(71.43)^2 )/0.7
#> [1] -1394.459

OOPS!!

P–G DSTN:

Need to convert \(p_0\), \(\mu\) and \(\sigma^2\) into \(\lambda, \alpha, \beta\). How (easily)?

BUT WHY? JUST USE THEORETICAL DISTN! Well, we wan rainfall values to use upstream in a simulation for (eg) cropping. MAXIMUM RAINFALL, with CI-like interval? Again… could do with distribution

PERHAPS CONNECT TO SOI

9.6 Exercises

Selected answers appear in Sect. E.9.

Exercise 9.1

  1. Medical Costs Observed variable: Annual medical expenses.

Latent variable (\(z\)): Underlying health need or risk.

Censoring: Many people incur \(0\) expenses in a given year, despite possibly having latent health risks or needs.

Interpretation: People with latent need below some threshold never seek care (e.g. due to costs, access, or asymptomatic cases), leading to observed \(0\).

Exercise 9.2

  1. Credit Card Balances Observed variable: Balance at end of month.

Latent variable (\(z\)): Willingness or propensity to use credit.

Censoring: Some users consistently pay in full and carry no balance.

Interpretation: Some people have low latent demand for borrowing; observed balance is zero if the latent borrowing desire is below threshold.

Exercise 9.3 Consider a latent variable \(Y\), and an observed variable \(X = \text{max}(0, Y)\). Suppose that \(Y\) has the normal distribution \[ Y \sim N(\mu = 1.5, \sigma^2 = 1), \] so that \(\operatorname{E}[Y] = 1.5\) and \(\operatorname{var}[Y] = 1\).

  1. Determine \(\Pr(Y < 0)\), where \(Z\) is a standard normal variate (Sect. 8.3.2).
  2. Using the functions \(\Phi(\cdot)\) and \(\phi(\cdot)\), determine the probability function for \(X\).
  3. Plot this probability function.
Peter K. Dunn, 2024: CC BY-NC-SA 4.0