E Selected solutions

This Appendix contains some answers to end-of-chapter questions.

E.1 Answers for Chap. 1

Answer to Exercise 1.3.

$\mathbb{C} = \{ a + bi \mid (a \in\mathbb{R})\cup (b \in\mathbb{R}) \cup (i^2 = -1)\}$.
$\mathbb{I} = \{ a + bi \mid (a = 0) \cup (b \in\mathbb{R}) \cup (i^2 = -1)\}$.

Answer to Exercise 1.4.

$S = \{ (a,b,c) \mid (a\in(-\infty, 0)\cap (0, \infty)), (-\infty < b < \infty), (-\infty < c < \infty)\}$, which can be written $X \in \{(a, b, c) | (a, b, c) \in \mathbb{R}, a \ne 0\}$ where $\mathbb{R}$ represents the real numbers.
The solutions to a quadratic equation are given by \[ x = \frac{-b \pm \sqrt{b^2 - 4ac} }{2a}. \] For two equal roots, $b^2 - 4ac = 0$, so event $R$ is defined as $R = \{ (a,b,c) \mid (a, b, c)\in \mathbb{R}, a\ne 0, b^2 - 4ac = 0\}$.
For no real roots, $b^2 - 4ac < 0$, so event $Z$ is defined as $Z = \{ (a,b,c) \mid (a, b, c)\in \mathbb{R}, a\ne 0, b^2 - 4ac < 0\}$.

Answer to Exercise 1.5.

$\{x \mid x^2 > 1\}$, or $\{x \mid (x < -1) \cup (x > 1)\}$.
$\{x \mid x^2 > 2\}$, or $\{x \mid (x < -\sqrt{2}) \cup (x > \sqrt{2} \}$.
$\varnothing$.

Answer to Exercise 1.6.

$A = \{ x \mid x\in S \cap P\}$.
$B = \{ x \mid x\in \bar{S} \cap P\}$.
$C = \{ x \mid x\in \bar{S} \cap \bar{P}\}$.

Answer to Exercise 1.7.

# Part 1
whereSetA <- which( substr(state.name,
                           start = 1,
                           stop = 1)
                    == "W")
SetA <- state.name[whereSetA]
SetA

# Part 2
whereSetB <- which( substr(state.name,
                           start = 1,
                           stop = 5)
                    == "North")
SetB <- state.name[whereSetB]
SetB

# Part 3
Length_State_Names <- nchar(state.name)
whereSetC <- which( substr(state.name,
                          start = Length_State_Names,
                          stop = Length_State_Names)
                   == "a")
SetC <- state.name[whereSetC]
SetC

# Part 4 
SetD <- union(SetC, SetA)
SetD

# Part 5
SetE <- intersect(SetC, SetA)
SetE

# Part 6
whereSetF <- which( substr(state.name,
                           start = 1,
                           stop = 1)
                   != "W")
SetF <- state.name[whereSetF]

SetG <- intersect(SetC, SetF )
SetG

Answer to Exercise 1.8.

head(state.x77)
#>            Population Income Illiteracy Life Exp
#> Alabama          3615   3624        2.1    69.05
#> Alaska            365   6315        1.5    69.31
#> Arizona          2212   4530        1.8    70.55
#> Arkansas         2110   3378        1.9    70.66
#> California      21198   5114        1.1    71.71
#> Colorado         2541   4884        0.7    72.06
#>            Murder HS Grad Frost   Area
#> Alabama      15.1    41.3    20  50708
#> Alaska       11.3    66.7   152 566432
#> Arizona       7.8    58.1    15 113417
#> Arkansas     10.1    39.9    65  51945
#> California   10.3    62.6    20 156361
#> Colorado      6.8    63.9   166 103766
state_Names <- rownames(state.x77)
# Part 1
SetA <- state_Names[ state.x77[, 4] > 70 ]
SetB <- state_Names[ state.x77[, 8] < 500000 ]
SetC <- state_Names[ state.x77[, 3] > 2 ]
SetD <- state_Names[ state.x77[, 6] < 50 ]
SetE <- intersect(SetC, SetD)
SetF <- union( SetC, SetD)

Answer to Exercise 1.9. $T = \{ x\in\mathbb{R} \mid x \ne 0\}$.

Answer to Exercise 1.10. $D = \{ x\in\mathbb{R} \mid x \ne \frac{\pi}{2} + n\pi, n \in\mathbb{Z}\}$.

Answer to Exercise 1.11. Set contains all real numbers strictly between $-2$ and $2$. $A$ is an uncountably infinite set.

Answer to Exercise 1.12. Set $B$ contains the integers: $B\in\mathbb{Z}$. Countably infinite cardinality: $|B| = |\mathbb{Z}| = \aleph_0$.

Answer to Exercise 1.13. \[\begin{align*} A\setminus(A\cap B) &= A\cap (A\cap B)^c\quad\text{(set difference)}\\ &= A\cap (A^c \cup B^c)\quad\text{(de Morgan's laws)}\\ &= (A\cap A^c) \cup (A\cap B^c)\quad\text{(distributive law)}\\ &= A\cap B^c. \end{align*}\]

Answer to Exercise 1.14. \[\begin{align*} (A\setminus B)^c &= (A\cap B^c)^c\text{(set difference)}\\ &= A^c \cup (B^c)^c\quad\text{(do Morgan's law)}\\ &= A^c\cap B\quad\text{(definition of complement)}. \end{align*}\]

Answer to Exercise 1.15. $[ (A\cup B) \cap (A\cup B^c) ]\cap B = [ A\cup(B\cap B^c) ] \cap B = [ A\cup \varnothing] \cap B = A\cap B$.

Answer to Exercise 1.16. $(A\cap B) \cup (A\cap B^c) = A \cap (B\cup B^c) = A\cap S = A$.

Answer to Exercise 1.18. $C = \{(x, y) \mid (x \in S) \cap (y \in D)\}$.

E.2 Answers for Chap. 2

Answer to Exercise 2.1.

Probably the Venn diagram is best.
$\Pr(A\cup B) = \Pr(A) + \Pr(B) - \Pr(A\cap B) = 0.66$.
$0.13$.
$0.89$.
$0.11/0.24 \approx 0.4583...$
$\Pr(A) \times \Pr(B) = 0.53\times 0.24 = 0.1272 \ne \Pr(A\cap B) = 0.11$; not independent… but close.

Answer to Exercise 2.2.

$(50/100)\times (49/99)\times (48/98)\times (47/97) = C^{50}_4 / ^{100}C_4\approx 0.0587$.
$C^{50}_2\times C^{50}_2 / C^{100}_4 = 1225/3201 \approx 0.3826$.
$\Pr(\text{at least 2 odd before 1st even}) = \Pr(\text{odd, odd, even, either}) + \Pr(\text{odd, odd, odd, even)} = (50/100)\times(49/99)\times(50/98) + (50/100)\times (49/99)\times(48/98)\times(50/97) \approx 0.1887$.
$\Pr(\text{sum odd}) = \Pr(\text{exactly 1 odd number drawn, OR exactly 3 odd numbers drawn}) = 1600/3201 \approx 0.49984$.

Answer to Exercise 2.3.

The length of time (in seconds) between green lights at the intersection, say $G$.
$S = \{G \mid 15 \le G \le 150\}$.
No—no equally likely events are defined.
The probability can be approximated—observe the lights many times, and count how often there is less than 90 seconds between green lights.

Answer to Exercise 2.4.

$C^7_5 \times C^5_4 \times C^2_1 \times C^1_1 = 210$.
$11^2 + (2\times 22) = 165$.

Answer to Exercise 2.5.

Tree diagram: Fig. E.1; table: Table E.1; Venn diagram: Fig. E.2.

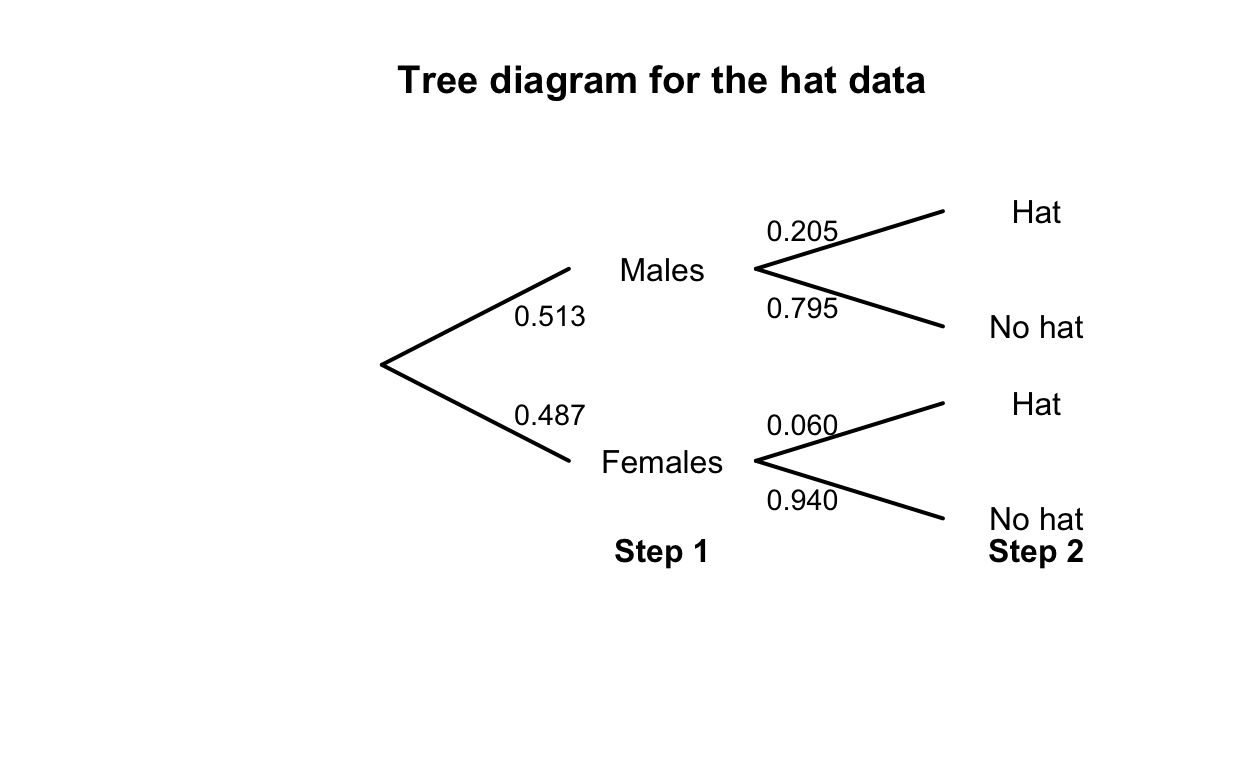
FIGURE E.1: Tree diagram for the hat-wearing example

TABLE E.1: The numbers of males and females wearing a hat in the middle of the day in Brisbane
	No Hat	Hat	Total
Males	307	79	386
Females	344	22	366

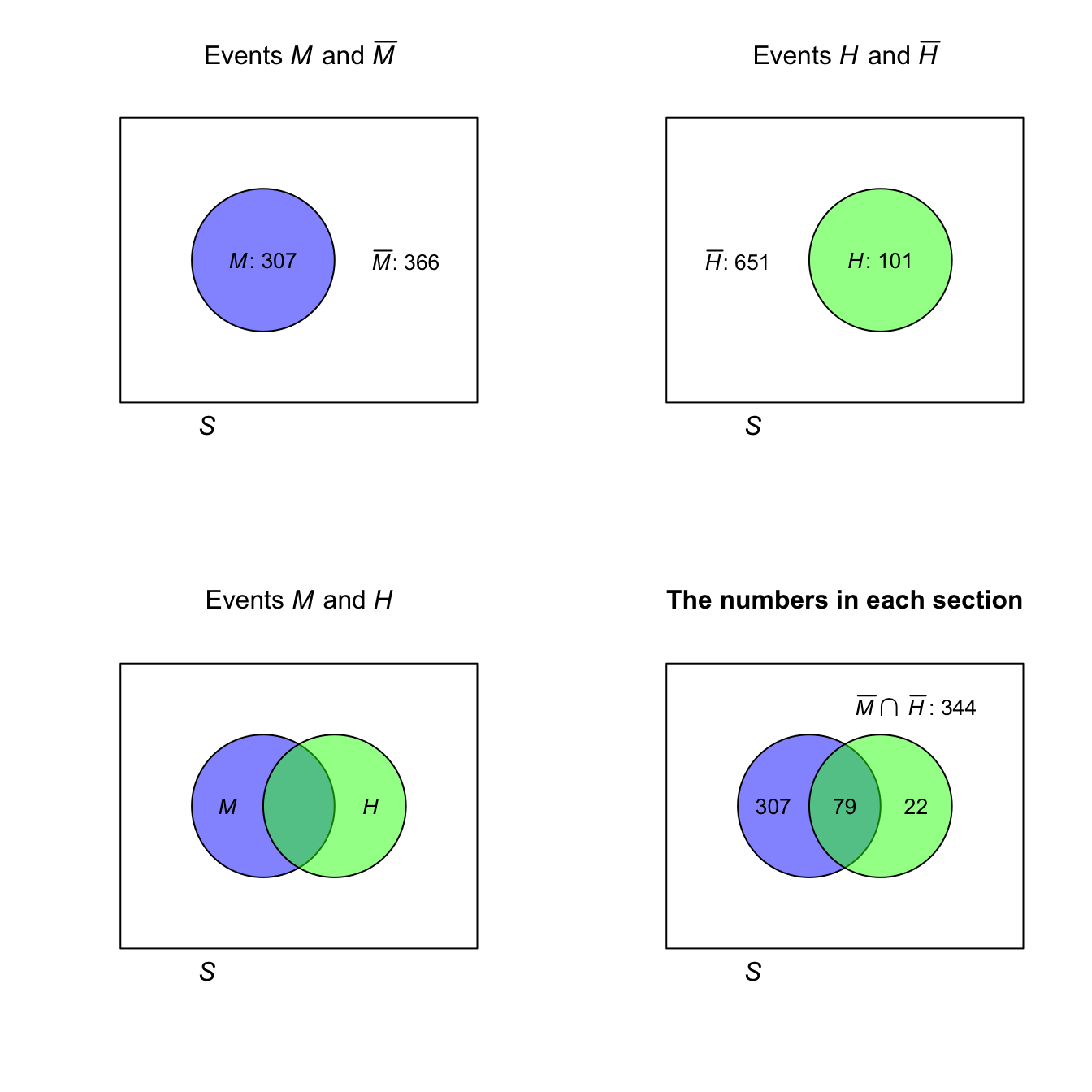
FIGURE E.2: The hat-wearing data as a Venn diagram

Answer to Exercise 2.6.

Choose one driver, and the other seven passengers can sit anywhere: $2!\times 7! = 10\,080$.
Choose one driver, and the other seven passengers can sit anywhere: $3!\times 7! = 30\,240$.
Choose one driver, choose who sits in what car sets, and the other five passengers can sit anywhere: $2!\times 2! \times 5! = 480$.

Answer to Exercise 2.7. $8\times 7\times 6\times 5 = 1680$ ways.

Answer to Exercise 2.8. The order is important; use permutations.

Eight: $^{26}P_8 = 62\,990\,928\,000$; nine: $^{26}P_9 = 1.133837\times 10^{12}$; ten: $^{26}P_8 = 1.927522\times 10^{13}$. Total: $2.047205\times 10^{13}$.
$^{52}P_8 = 3.034234\times 10^{13}$.
$^{62}P_8 = 1.363259\times 10^{14}$.
No answer (yet).

Answer to Exercise 2.9.

()() and (()). There are two ways.
()()() and (())() and ()(()) and ((())) and (()()). There are five ways.
$\displaystyle \frac{1}{n + 1} \binom{2n}{n} = \frac{1}{n + 1}\frac{(2n)!}{n!n!} = \frac{1}{(n + 1)!} \frac{(2n)!}{n!}$ as to be shown.
Write as $\displaystyle \frac{(2n)!}{n!\, n!} - \frac{(2n)!}{(n + 1)! (2n - n - 1)!}$. Simplifying: \[\begin{align*} \frac{(2n)!}{n!\, n!} - \frac{(2n)!}{(n + 1)! (n - 1)!} &= \frac{(2n)!}{n!\, n!} - \left( \frac{n}{n + 1}\right) \frac{(2n)!}{n!\,n!}\\ &= \binom{2n}{n}\left(1 - \frac{n}{n + 1}\right) \\ &= \frac{1}{n + 1} \binom{2n}{n} \end{align*}\]
The first nine Catalan numbers, for $n = 0, \dots 8$, are $1, 1, 2, 5, 14, 42, 132, 429, 1430$

Answer to Exercise 2.10. See Fig. E.3.

# Define a function to compute Stirling numbers:
stirling <- function(n){ 
  sqrt(2 * pi *n) * (n/exp(1))^n
}

n <- 1:10
Actual <- factorial(n) 
Approx <- stirling(n)
RelError <- (Actual - Approx)/Actual * 100

cbind(Actual, Approx, RelError)
#>        Actual       Approx  RelError
#>  [1,]       1 9.221370e-01 7.7862991
#>  [2,]       2 1.919004e+00 4.0497824
#>  [3,]       6 5.836210e+00 2.7298401
#>  [4,]      24 2.350618e+01 2.0576036
#>  [5,]     120 1.180192e+02 1.6506934
#>  [6,]     720 7.100782e+02 1.3780299
#>  [7,]    5040 4.980396e+03 1.1826224
#>  [8,]   40320 3.990240e+04 1.0357256
#>  [9,]  362880 3.595369e+05 0.9212762
#> [10,] 3628800 3.598696e+06 0.8295960

plot(RelError ~ n,
     ylim = c(0, 8),
     las = 1, 
     type = "b",
     pch = 19,
     lwd = 2,
     xlab = expression(italic(n)),
     ylab = "Relative error (%)",
     main = "Relative error of\nStirling's approximation")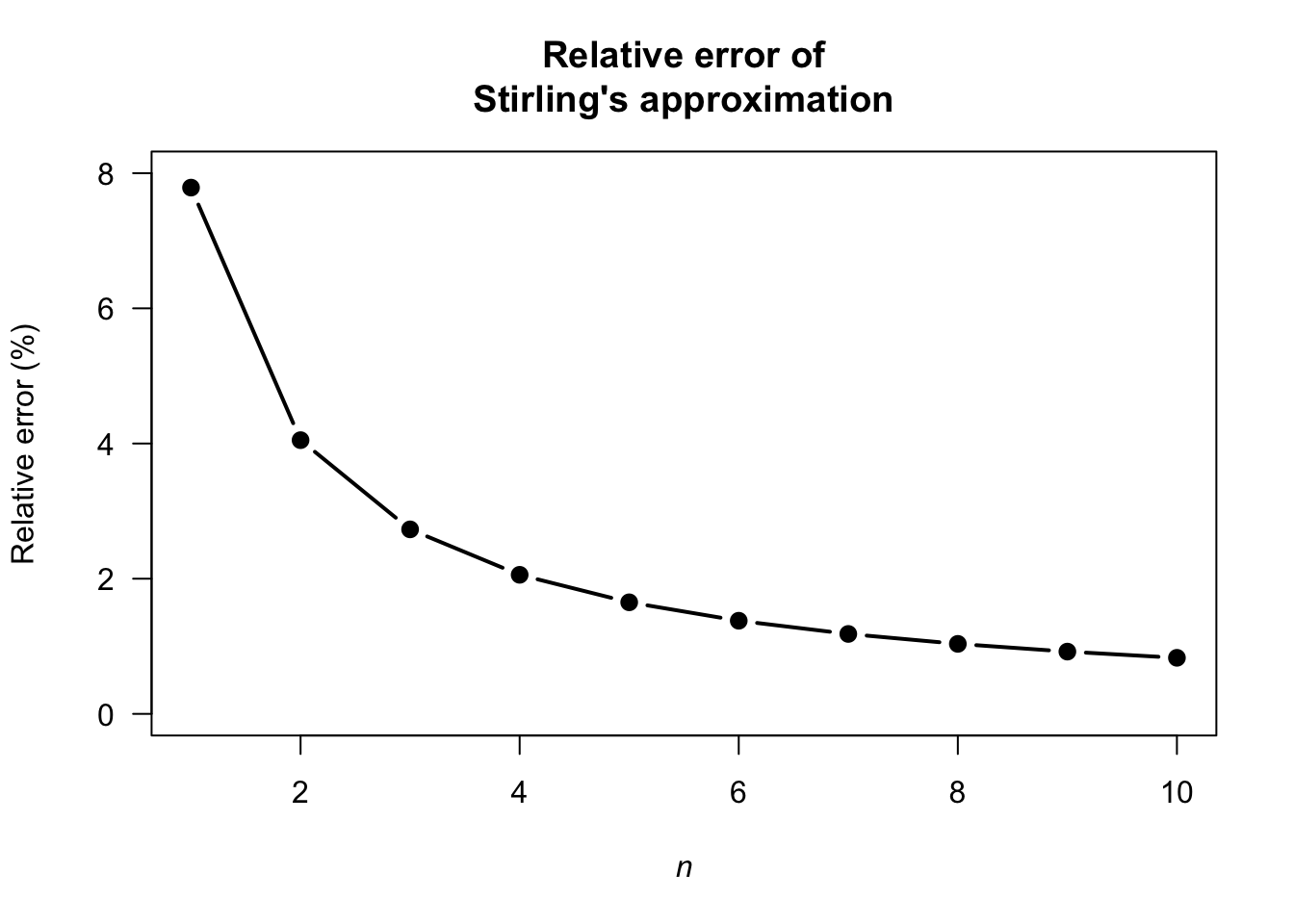

FIGURE E.3: Relative error of Stirling’s approximation

Answer to Exercise 2.11.

$\Pr(\text{Player throwing first wins})$ means $\Pr(\text{First six on throw 1 or 3 or 5 or ...})$. So: $\Pr(\text{First six on throw 1}) + \Pr(\text{First six on throw 3}) + \cdots$. This produces a geometric progression that can be summed obtained (see App. B).
Use Theorem 2.4. Define the events $A = \text{Player 1 wins}$, $B_1 = \text{Player 1 throws first}$, and $B_2 = \text{Player 1 throws second}$.

Answer to Exercise 2.12.

Write $y = \Pr(\text{answers `yes'})$.

Then, from a tree diagram (Step 1: Used drugs/did not use drugs; Step 2: Card says “Used drugs”/Card says “Did not use drugs”):

\[\begin{align*} y &= \Pr(\text{Never takes drugs and say so}) + \Pr(\text{Takes drugs and says so})\\ &= (1 - p) \times\left(\frac{N - m}{N}\right) + p\times\frac{m}{N}. \end{align*}\] Solving for the unknown $p$: \[ p = \frac{yN - N + m}{2m - N}. \] 2. When $m = 0$, $\Pr(Y) = p$: This mean every card says ‘I have used an illegal drug in the past twelve months’, so the proportion that have used an illegal drug is just the same as the proportion responding with ‘Yes’ (and there is no anonymity). When $m = 0$, $\Pr(Y) = 1 - p$: This mean every card says ‘I have not used an illegal drug in the past twelve months’, so the proportion that have used an illegal drug is just the same as the proportion responding with ‘No’ (and there is no anonymity). When $m = N/2$, $\Pr(Y) = 0.5$; we have learnt nothing: The probability is 50–50. 3. $\displaystyle d = \frac{yN - N + m}{2m - N}$, so plugging in $N = 100$, $m = 25$ and $\Pr(Y) = 175/400 = 0.4375$ gives $d = 0.625$.

Answer to Exercise 2.13.

Use Theorem 2.4 to find $\Pr(C)$ where $C = \text{select correct answer}$, $K = \text{student knows answer}$. Then, $\Pr(C) =\displaystyle {\frac{mp + q}{m}}$

Answer to Exercise 2.14.

$\Pr(W)$ means ‘the probability of a win’. $\Pr(W \mid D^c)$ means ‘the probability of a win, given that the game was not a draw’.
$\Pr(W) = 91/208 = 0.4375$. $\Pr(W\mid D^c) = 91/(208 - 50) = 0.5759494$.

Answer to Exercise 2.15. Write $d$ as the distance; then $S = \{d: 0 \le d \le \sqrt{2}\}$. For the grid, let’s use R to find what values are possible:

x <- y <- seq(0, 1, by = 0.25)

distances <- outer(x, y, function(x, y){sqrt(x^2 + y^2)})

unique(sort(distances))
#>  [1] 0.0000000 0.2500000 0.3535534 0.5000000
#>  [5] 0.5590170 0.7071068 0.7500000 0.7905694
#>  [9] 0.9013878 1.0000000 1.0307764 1.0606602
#> [13] 1.1180340 1.2500000 1.4142136

It seems there are 15 possible values for the distance:

$0$, $0.25$, $0.50$, $0.75$ and $1$ along grid lines;
$\sqrt{2}/4$, $\sqrt{5}/4$, $\sqrt{10}/4$ and $\sqrt{17}/4$ when the line is moved one grid-square right;
$\sqrt{13}/4$ and $\sqrt{20}/4$ when the line is moved two grid-squares right;
$\sqrt{25}/4$ when the line is moved three grid-squares right;

and so on.

Answer to Exercise 2.16.

Anywhere between $0$% and $8$%.
$0.06/0.30 = 0.20$.
$0.06/0.08 = 0.75$.

Answer to Exercise 2.17. The total number of children: $69\,279$. Define $N$ as ‘a first-nations student’, $F$ as ‘a female student’, and $G$ as ‘attends a government school’.

$(2540 + 2734 + 391 + 362) / 69,279 \approx 0.0870$.
$49,067/69,279 \approx 0.708$.
Females: prob FN: $0.107$; Males: prob FN: $0.108$; close to independent.
Females: prob FN: $0.040$; Males: prob FN: $0.035$; close to independent.
Gov: prob FN: $0.107$; NGov: prob FN: $0.040$; not independent.
Gov: prob FN: $0.108$; NGov: prob FN: $0.035$; not independent.
Regardless of sex, First Nations children more likely to be at government school.

Answer to Exercise 2.18.

The probability depends on what happens with the first card: \[\begin{align*} \Pr(\text{Ace second}) &= \Pr(\text{Ace, then Ace}) + \Pr(\text{Non-Ace, then Ace})\\ &= \left(\frac{4}{52}\times \frac{3}{51}\right) + \left(\frac{48}{52}\times \frac{4}{51}\right) \\ &= \frac{204}{52\times 51} \approx 0.07843. \end{align*}\] You can use a tree diagram, for example.
Be careful:

\[\begin{align*} &\Pr(\text{1st card lower rank than second card})\\ &= \Pr(\text{2nd card a K}) \times \Pr(\text{1st card from Q to Ace}) + {}\\ &\qquad \Pr(\text{2nd card a Q}) \times \Pr(\text{1st card from J to Ace}) +{}\\ &\qquad \Pr(\text{2nd card a J}) \times \Pr(\text{1st card from 10 to Ace}) + \dots + {}\\ &\qquad \Pr(\text{2nd card a 2}) \times \Pr(\text{1st card an Ace}) \\ &= \frac{4}{51} \times \frac{12\times 4}{52} + {}\\ &\qquad \frac{4}{51} \times \frac{11\times 4}{52} +\\ &\qquad \frac{4}{51} \times \frac{10\times 4}{52} + \dots +\\ &\qquad \frac{4}{51} \times \frac{1\times 4}{52} \\ &= \frac{4}{51}\frac{4}{52}\left[ 12 + 11 + 10 + \cdots + 1\right]\\ &= \frac{4}{51}\frac{4}{52} \frac{13\times 12}{2} \approx 0.4705882. \end{align*}\] 3. We can select any of the $52$ cards to begin. Then, there are four cards higher and four lower, so a total of $16 options for the second card, a total of $52\times 16 = 832$ ways it can happen. The number of ways of getting two cards is $52\times 51 = 2652$, so the probability is $832/2652 \approx 0.3137$.

Answer to Exercise 2.19. No answer (yet).

Answer to Exercise 2.20. $x = 0.05$.

Answer to Exercise 2.21.

\[\begin{align*} 12\times {}^7P_k &= 7\times {}^6P_{k + 1} \\ 12\times \frac{7!}{(7 - k)!} &= 7\times\frac{6!}{(5 - k)!}\\ \frac{12}{(7 - k)!} &= \frac{1}{(5 - k)!}\\ \frac{12}{(7 - k)\times (6 - k)\times (5 - k)!} &= \frac{1}{(5 - k)!}\\ 12 &= (7 - k)(6 - k)\\ k^2 - 13k + 30 &= 0\\ (k - 10)(k - 3) &= 0 \end{align*}\] and so $k = 10$ or $k = 3$. But if $k = 10$, we get silly things like $P^7_{10}$. So the solution must be $k = 3$.

for (k in (1:5)){ # Answer must e less than 6
  cat("FOR k = ", k, ":")
  cat("LHS =", 12 * factorial(7) / factorial(7 - k), "; ")
  cat("RHS =", 7 * factorial(6) / factorial(5 - k), "\n")
}
#> FOR k =  1 :LHS = 84 ; RHS = 210 
#> FOR k =  2 :LHS = 504 ; RHS = 840 
#> FOR k =  3 :LHS = 2520 ; RHS = 2520 
#> FOR k =  4 :LHS = 10080 ; RHS = 5040 
#> FOR k =  5 :LHS = 30240 ; RHS = 5040

Answer to Exercise 2.22.

\[\begin{align*} \frac{ {}^7 P_{r + 1}}{ {}^{7}C_r} &= \frac{7!}{(7 - (r + 1))!} \times \frac{(7 - r)!\, r!}{7!}\\ &= \frac{7!}{(6 - r)!} \times \frac{(7 - r)!\, r!}{7!}\\ &= \frac{(7 - r)!\, r!}{(6 - r)!}\\ &= \frac{(7 - r)\times (6 - r)!\, r!}{(6 - r)!}\\ &= (7 - r) r!\\ &= 10. \end{align*}\] Rewrite: $r! = 10/(7 - r)$. Since $r!$ is a positive integer, $r$ must be either $r = 2$ or $r = 5$. Trying both, clearly $r = 2$.

Answer to Exercise 2.23.

Proceed: \[\begin{align*} \Pr(\text{at least two same birthday}) &= 1 - \Pr(\text{no two birthdays same}) \\ &= 1 - \Pr(\text{every birthday different}) \\ &= 1 - \left(\frac{365}{365}\right) \times \left(\frac{364}{365}\right) \times \left(\frac{363}{365}\right) \times \cdots \times \left(\frac{365 - n + 1}{365}\right)\\ &= 1 - \left(\frac{1}{365}\right)^{n} \times (365\times 364 \times\cdots (365 - n + 1) ) \end{align*}\]
Graph the relationship for various values of $N$ (from $2$ to $60$), using the above form to compute the probability.
No answer (yet).
Birthdays are independent and randomly occur through the year (i.e., each day is equally likely).

N <- 2:80
probs <- array( dim = length(N) )

for (i in 1:length(N)){
  
  probs[i] <- 1 - prod( (365 - (1:N[i]) + 1)/365 )

}
plot( probs  ~ N,
      type = "l",
      lwd = 2,
      ylab = "Prob. at least two share birthday",
      xlab = expression(Group~size~italic(N)),
      las = 1)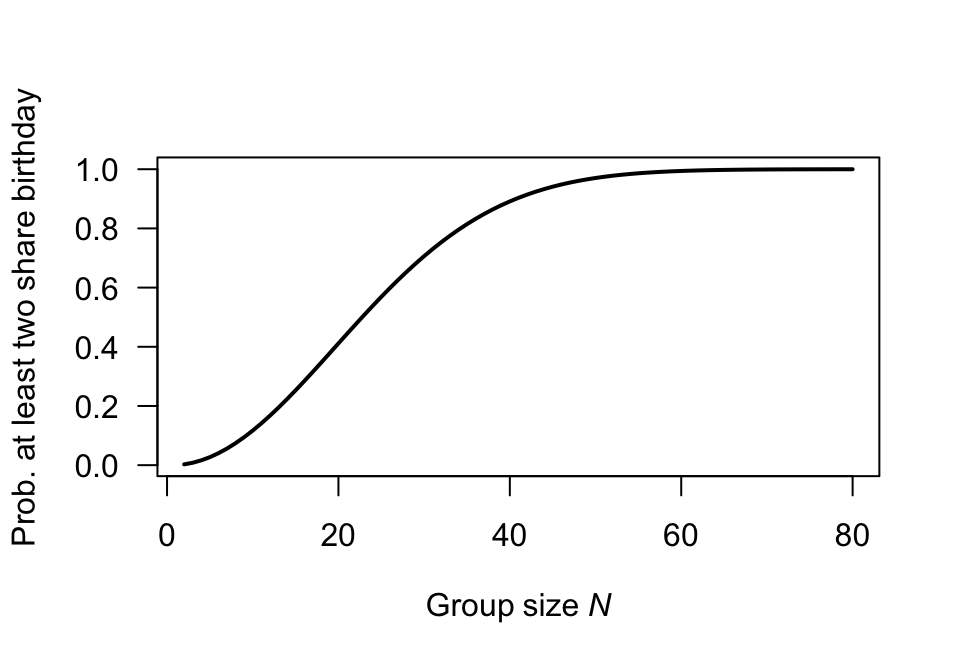

FIGURE E.4: Question 1

Answer to Exercise 2.24.

set.seed(981686)
numberSimulations <- 5000
anyConsecutive <- 0

for (i in (1:numberSimulations)){
  # Find the six numbers
  theNumbers <- sample(1:45,
                       size = 6,
                       replace = FALSE)
  theNumbers <- sort(theNumbers)
  
  if (any( diff(theNumbers) == 1 )){
    anyConsecutive <- anyConsecutive + 1
  }
  
}
cat("Number with consecutive values", 
    anyConsecutive,"\n")
#> Number with consecutive values 2691
cat("Proportion with consecutive values", 
    round(anyConsecutive/numberSimulations, 3), "\n")
#> Proportion with consecutive values 0.538
cat("Proportion WITHOUT consecutive values", 
    round(1 - anyConsecutive/numberSimulations, 3), "\n")
#> Proportion WITHOUT consecutive values 0.462

Answer to Exercise 2.25. $\Pr( A^c \cap B^c) = 0.5$ (using, for example, a two-way table). $A$ and $B$ are not independent.

Answer to Exercise 2.26. Use two-way table, or Venn diagrams.

Answer to Exercise 2.27. $7\times 3\times 2 = 42$.

Answer to Exercise 2.28. $10\times 10\times 10\times 26\times 26\times 10 = 6\ 760\ 000$.

Answer to Exercise 2.29. Order is not important, so combinations are relevant.

There are $\binom{52}{5} = 2\,598\,960$ ways to get five cards from $52$ (without replacement).

Pick the denomination: $13$ to select from. We need two of those $4$ cards: $13\times \binom{4}{2}$. Now the other three cards are drawn from the other $12$ denominations: $\binom{12}{3}$. There are also $4$ ways to choose the suit of each of those $3$ cards. All up then: the number of ways is $13\times\binom{4}{2}\times\binom{12}{3}\times 4^3 = 1\,098\,240$. The probability is therefore $1\,098\,240/2\,598\,960 = 0.422569$. TAKE THE THREE OF A KIND AND FOUR OF A KIND!!
There are $4$ suits each with $4$ picture cards, so $16$ picture cards in total. We want to select five picture cards from $52$ cards, without replacement: $^{16}C_5 = 4\,368$ ways to do this. So the probability is $4\,368\ 160/^{52}C_5 = 0.0017$.

Answer to Exercise 2.31. $\binom{25}{8}/\binom{26}{6} = (25!\, 6!\, 19!)/(8!\,17!\,25!) = 171/28 \approx 6.107$.

Answer to Exercise 2.33. No answer (yet).

Answer to Exercise 2.34. The key: $P$ must lie on a semi-circle with diameter $AB$.

Answer to Exercise 2.37.

set.seed(123)

roll_die <- function(die, n) sample(die, n, replace = TRUE)

n <- 1e6
A <- c(2, 2, 4, 4, 9, 9)
B <- c(1, 1, 6, 6, 8, 8)
C <- c(3, 3, 5, 5, 7, 7)

# Simulate rolls
A_rolls <- roll_die(A, n)
B_rolls <- roll_die(B, n)
C_rolls <- roll_die(C, n)

# Compute win probabilities
p_A_beats_B <- mean(A_rolls > B_rolls)
p_B_beats_C <- mean(B_rolls > C_rolls)
p_C_beats_A <- mean(C_rolls > A_rolls)

c(
  "P(A > B)" = p_A_beats_B,
  "P(B > C)" = p_B_beats_C,
  "P(C > A)" = p_C_beats_A
)
#> P(A > B) P(B > C) P(C > A) 
#> 0.555105 0.555608 0.555870

Answer to Exercise 2.38. To appear.

Answer to Exercise 2.39.

Generate a random sequence of length $1000$ of the digits $1$, $2$ and $3$ to represent which door is hiding the car on each of $1000$ nights.
Generate another such sequence to represent the contestants first choice on each of the $1000$ nights (assumed chosen at random).
The number of times the numbers in the two lists of random numbers do agree represents the number of times the contestant will win if the contestant doesn’t change doors. If the numbers in the two columns don’t agree then the contestant will win only if the contestant decides to change doors.

Recall that the host selects a door that he or she knows does not contains the car.

Generate a random sequence of length $1000$ of the digits $1$, $2$ and $3$ to represent which door is hiding the car on each of $1000$ nights.
Generate another such sequence to represent the contestants first choice on each of the $1000$ nights (assumed chosen at random).
The host then opens a door not chosen by the contestant, that does not contain the car.
The contestant then select from one of the unopened doors.
The number of times the numbers in the two lists of random numbers do agree represents the number of times the contestant will win if the contestant doesn’t change doors. If the numbers in the two columns don’t agree then the contestant will win only if the contestant decides to change doors.

set.seed(93671)        # For reproducibility
num_Reps <- 1000       # Number of simulations

# Initialize counters
Win_By_Switching <- 0
Win_By_Staying   <- 0

for (i in 1:num_Reps) {

  # Step 1: Randomly place the car
  Car_Door <- sample(1:3, 1)

  # Step 2: CONTESTANT makes an initial choice
  First_Choice <- sample(1:3, 
                         size = 1)

  # Step 3: HOST then chooses to open a goat door and show contestant.
  #         Host chooses door *not* picked by contestant, or door *not* hiding car
  Possible_Reveals <- setdiff(1:3, 
                              c(First_Choice, Car_Door))

  # So Host may now have one or two options of door to open
  if (length(Possible_Reveals) == 1) {
    # With one option... just take it
    Host_Reveal <- Possible_Reveals
  }
  if (length(Possible_Reveals) == 2) {
    # With two options, select one
    Host_Reveal <- setdiff(1:3, 
                           First_Choice)
  }

  # Step 4: CONTESTANT may decide to switch to the other unopened door
  Remaining_Door <- setdiff(1:3, 
                            c(First_Choice, Host_Reveal))
  Switch_Choice <- Remaining_Door

  # Step 5: Check win conditions
  if (First_Choice == Car_Door) {
    Win_By_Staying <- Win_By_Staying + 1
  } else {
    if (Switch_Choice == Car_Door) {
       Win_By_Switching <- Win_By_Switching + 1
    }
  }
}

# Results
c(Win_By_Staying, Win_By_Switching) / num_Reps
#> [1] 0.336 0.664

E.3 Answers for Chap. 3

Answer to Exercise 3.1.

$R_X = \{X \mid x \in (0, 1, 2) \}$; discrete.
$R_X = \{X \mid x \in (1, 2, 3\dots) \}$; discrete.
$R_X = \{X \mid x \in (0, \infty) \}$; continuous.
$R_X = \{X \mid x \in (0, \infty) \}$; continuous.

Answer to Exercise 3.2.

$R_X = \{X \mid x \in (0, 1, 2, \dots) \}$; discrete.
$R_X = \{X \mid x \in (0, 1, 2, \dots) \}$; discrete.
$R_X = \{X \mid x \in (0, \infty) \}$; continuous.
$R_X = \{X \mid x \in [0, \infty) \}$; mixed.

Answer to Exercise 3.3.

The sum of all probabilities is one, and none are negative.
$\displaystyle F_X(x) = \begin{cases} 0 & \text{for $x < 10$};\\ 0.3 & \text{for $10 \le x < 15$};\\ 0.5 & \text{for $15 \le x < 20$};\\ 1 & \text{for $x \ge 20$}. \end{cases}$
$\Pr(X > 13) = 1 - F_X(13) = 0.7$.
$\Pr(X \le 10 \mid X\le 15) = \Pr(X \le 10) / \Pr(X \le 15) = F_X(10)/F_X(15) = 0.3/0.5 = 0.6$.

Answer to Exercise 3.4.

All probabilities are non-negative. Also: $\sum_{x=0}^\infty p_X(x) = \frac{1}{2} + \frac{1}{2}\left(\frac{1}{2}\right) + \frac{1}{2}\left(\frac{1}{2}\right)^2 + \frac{1}{2}\left(\frac{1}{2}\right)^3 + \cdots$. Using Equation (B.5)), with $a = 1/2$ and $r = 1/2$, the sum of this series is $\sum_{x=0}^\infty p_X(x) = 1$. $p_X(s)$ is a valid PDF.

Answer to Exercise 3.5.

$\alpha = 2/15$.
$\displaystyle F_Z(z) = \begin{cases} 0 & \text{for $z \le -1$};\\ 6z/15 - z^2/15 + 7/15 & \text{for $-1 < z < 2$};\\ 1 & \text{for $z \ge 2$}. \end{cases}$
$\Pr(Z < 0) = F_Z(0) = 7/15 \approx 0.4666$.

F1 <- function(x){
  F <- array( dim = length(x))
  F[ x < -1] <- 0
  F[ x > 2] <- 1
  Interesting <- (x > -1) & (x < 2)
  F[ Interesting ] <- 6*z[Interesting]/15 - (z[Interesting]^2)/15 + 7/15
  F
}

z <- seq(-2, 3, 
         length = 200)
plot( F1(z) ~ z,
      las = 1,
      type = "l",
      xlab = expression(italic(x)),
      ylab = "Dist. fn.",
      lwd = 2)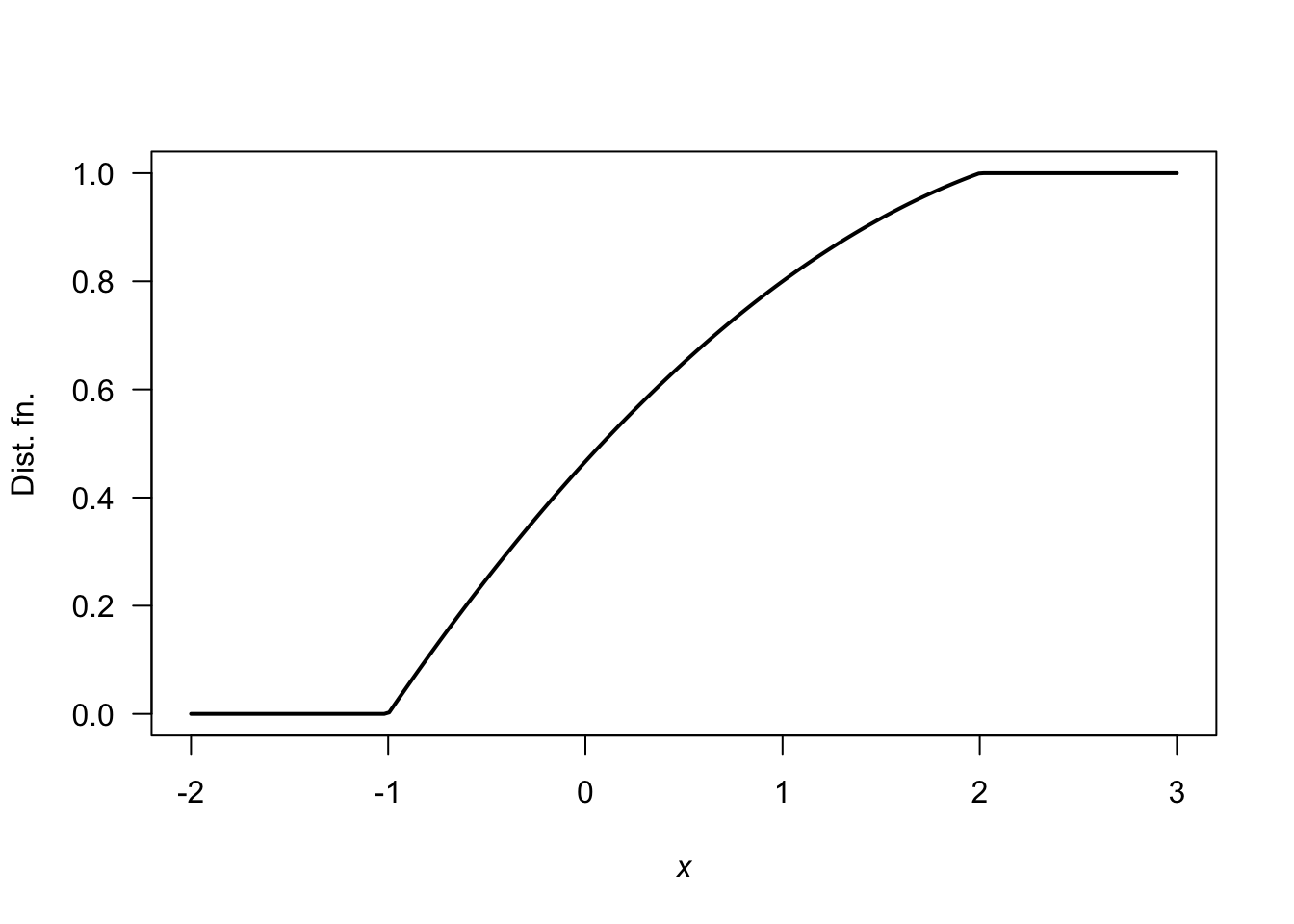

FIGURE E.5: The DF for $f(z)$

Answer to Exercise 3.6. 1. $F_X(x) = 0$ for $y \le 0$; $F_x(x) = (12 - y^2)y/16$ for $0 < y < 2$; $F_X(x) = 1$ for $y \ge 2$. 2. $11/16$.

Answer to Exercise 3.7. 1. $p = 0.5$. 1. See below. 1. For $y < 0$, $F_Y(y) = 0$; for $y = 0$, $F_Y(y) = 0.5$; for $0 < y < 1$, $F_Y(y) = (1 - y^2 + 2y)/2$; for $y \ge 1$, $F_Y(y) = 1$. 1. $1/8$.

Answer to Exercise 3.8. 1. $c = 0.25$. 1. See below. 1. For $x < 0$, $F_X(x) = 0$; for $x = 0$, $F_X(x) = 0.25$; for $0 < x \ge 1$, $F_X(x) = (1 + x^2)/4$; for $1 < x \ge 3$, $F_X(x) = (6x - 1 - x^2)/8$; for $x > 3$, $F_X(x) = 1$. 1. $1/2$.

Answer to Exercise 3.9. $\alpha = 2$, so $f_Y(y) = y^2 - 2$ for $y = 1, 2$.

Answer to Exercise 3.10. Solving for the mass function to give a total area of one gives $b = -2$. But this produces a negative probability for $x = -2$, so there is no value for $b$ which produces a valid probability function.

Answer to Exercise 3.11. $a = 2/3$.

Answer to Exercise 3.12. $a = 2/\sqrt{2 + \pi}\approx 0.8820$$.

Answer to Exercise 3.13.

$\displaystyle p_W(w) = \begin{cases} 0.3 & \text{for $w = 10$};\\ 0.4 & \text{for $w = 20$};\\ 0.2 & \text{for $w = 30$};\\ 0.1 & \text{for $w = 40$};\\ 0 & \text{elsewhere}. \end{cases}$
$\Pr(W < 25) = 0.7$.

Answer to Exercise 3.14.

$\displaystyle f_Y(y) = \begin{cases} (4/3) - y^2 & \text{for $0 < y < 1$};\\ 0 & \text{elsewhere}. \end{cases}$
$\Pr(Y < 0.5) = 0.625$.

fy <- function(y){
  PDFy <- array(0, dim = length(y))
  PDFy <- ifelse( (y > 0) & (y < 1),
                  (4/3) - y^2,
                  0)
  PDFy
}
y <- seq(-1, 2,
         length = 500)
plot(fy(y) ~ y,
     lwd = 2,
     type = "l",
     xlab = expression(italic(y)),
     ylab = "PDF",
     las = 1)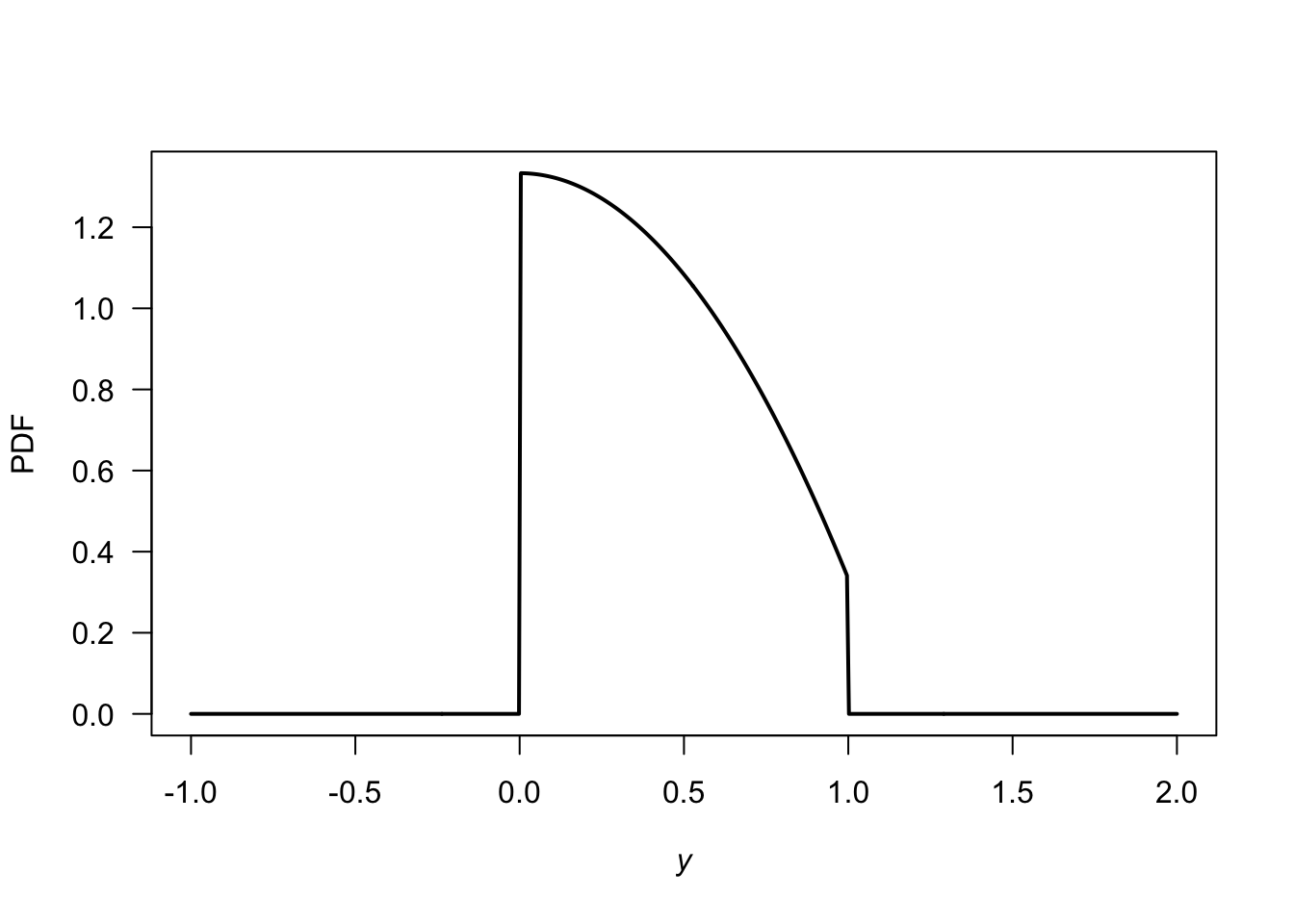

FIGURE E.6: A PDF

Answer to Exercise 3.15.

Easiest to draw, and see that this represents a triangular distribution, and find the area of the said triangle. Integration can be used though.
PDF: \[\begin{align*} f_X(x) &= \begin{cases} \frac{2}{8.8\times 4.4} (x - 0.6) & \text{for $0.6 < x < 5$};\\ \frac{2}{8.8\times 4.4} (9.4 - x) & \text{for $5 < x < 9.4$} \end{cases}\\ &= \begin{cases} \frac{2}{38.72} (x - 0.6) & \text{for $0.6 < x < 5$};\\ \frac{2}{38.72} (9.4 - x) & \text{for $5 < x < 9.4$}. \end{cases} \end{align*}\]
Proceed: \[\begin{align*} F_X(x) &= \begin{cases} 0 & \text{for $x < 0.6$}\\ \int_{0.6}^x \frac{2}{38.72} (t - 0.6) \, dt & \text{for $0.6 \le x < 5$};\\ \int_5^x \frac{2}{38.72} (9.4 - t)\, dt + 0.5 & \text{for $5 \le x < 9.4$}.\\ 1 & \text{for $x \ge 9.4$} \end{cases}\\ &= \begin{cases} 0 & \text{for $x < 0.6$}\\ [(0.6 - x)^2 ]/ 38.72 & \text{for $0.6 \le x < 5$};\\ 1 - [(x - 9.4)^2] / 38.72 & \text{for $5 \le x < 9.4$}.\\ 1 & \text{for $x \ge 9.4$} \end{cases} \end{align*}\]
See below.
$\Pr(X > 3) = 1 - \Pr(X < 3) = 1 - 0.1487603 = 0.8512397$ (or use areas of triangles)
$\Pr(X > 3 \mid X > 1) = \Pr(X > 3) / \Pr(X > 1) = 0.8512397 / 0.9958678 = 0.8547718$.
One is just if $X$ exceeds 3; the other if $X$ exceeds 3 if we already know $X$ has exceeded 1.

f <- function(x){
  f <- array( dim = length(x))
  f[x < 0.6] <- 0
  f[x > 9.4] <- 0
  xSmall <- (x >= 0.6) & ( x <= 5)
  xLarge <- (x > 5) & (x <= 9.4)
  f[xSmall] <- 2 / (8.8 * 4.4) * (x[xSmall] - 0.6)
  f[xLarge] <- 2 / (8.8 * 4.4) * (9.4 - x[xLarge] )
  f
}

F <- function(x){
  FF <- array( dim = length(x))

  for (i in (1:length(x))){
    FF[i] <- integrate(f, lower = 0.6, upper = x[i])$value
  }
  FF
}


par(mfrow = c(1, 2))
x <- seq(0, 10,
         length = 200)
plot( f(x) ~ x,
      type = "l",
      lwd = 2,
      las = 1,
      main = "PROB fn",
      xlab = expression(italic(x)),
      ylab = "Prob. fn.")



x <- seq(0, 10,
         length = 200)
plot( F(x) ~ x,
      type = "l",
      lwd = 2,
      las = 1,
      main = "DIST fn",
      xlab = expression(italic(x)),
      ylab = "Dist fn.")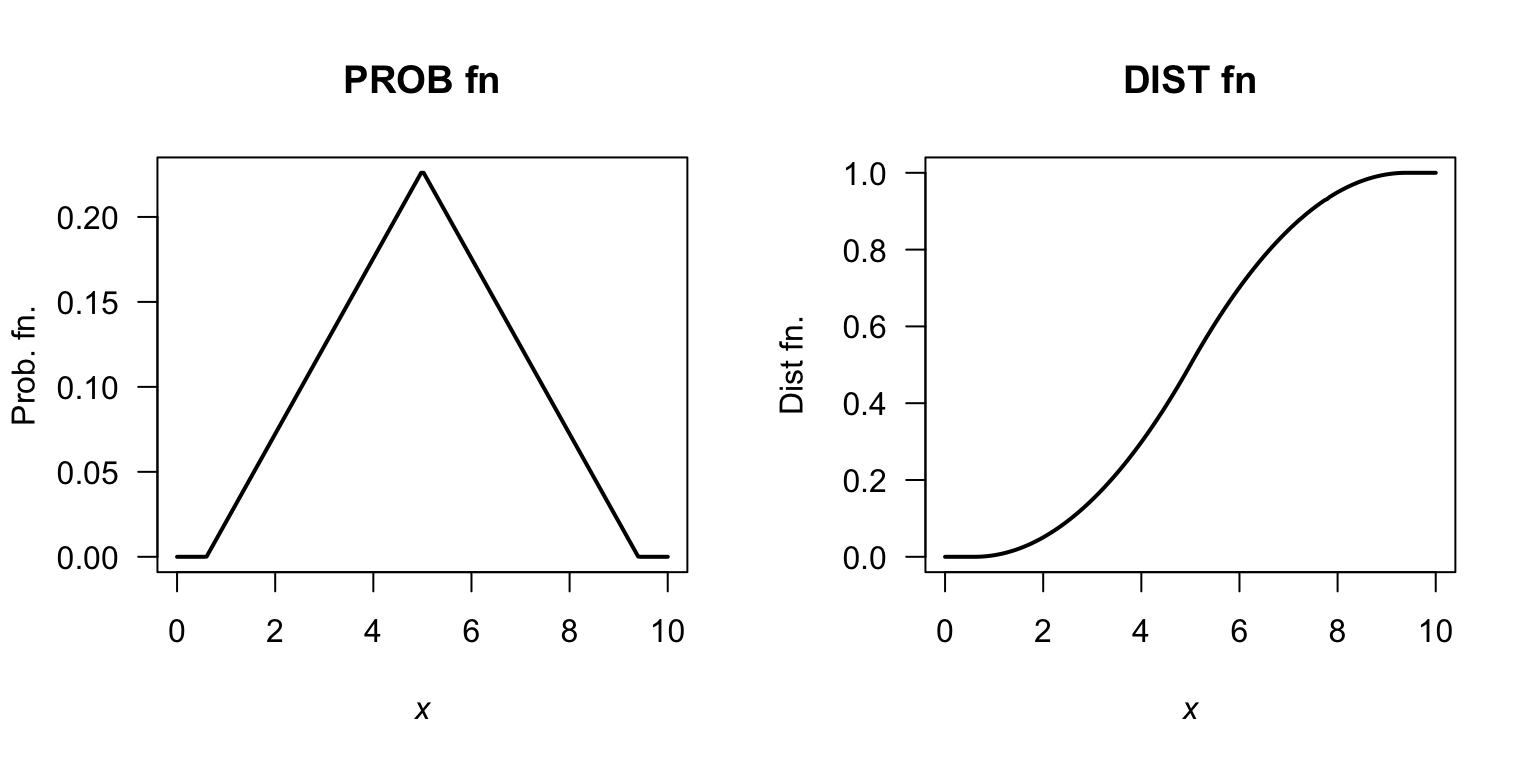

FIGURE E.7: A PDF and DF

1 - F(3)
#> [1] 0.8512397
(1 - F(3)) / (1 - F(1))
#> [1] 0.8547718

Answer to Exercise 3.16.

Using the area of triangles, the ‘height’ is $2/27 \approx 0.07407407$ as shown below. Then, after some algebra: \[ f_S(s) = \begin{cases} \frac{4}{81}s - \frac{14}{81} & \text{for $3.5 < s < 5$};\\ -\frac{4}{1377}s + \frac{122}{1377} & \text{for $5 < s < 30.5$}. \end{cases} \] Also, \[ F_S(s) = \begin{cases} 0 & \text{for $s < 3.5$};\\ \frac{(7 - 2s)^2}{162} & \text{for $3.5 < s < 5$};\\ \frac{2}{1377} (s^2 - 61s + 280) & \text{for $5 < s < 30.5$};\\ 1 & \text{for $s > 30.5$}. \end{cases} \] Then, $\Pr(S > 20 \mid S > 10) = \Pr( (S > 20) \cap (S > 10) )/\Pr(S > 10) = \Pr(S > 20)/\Pr(S > 10) = 0.1601311 / 0.6103854$. This is about $0.2623$.

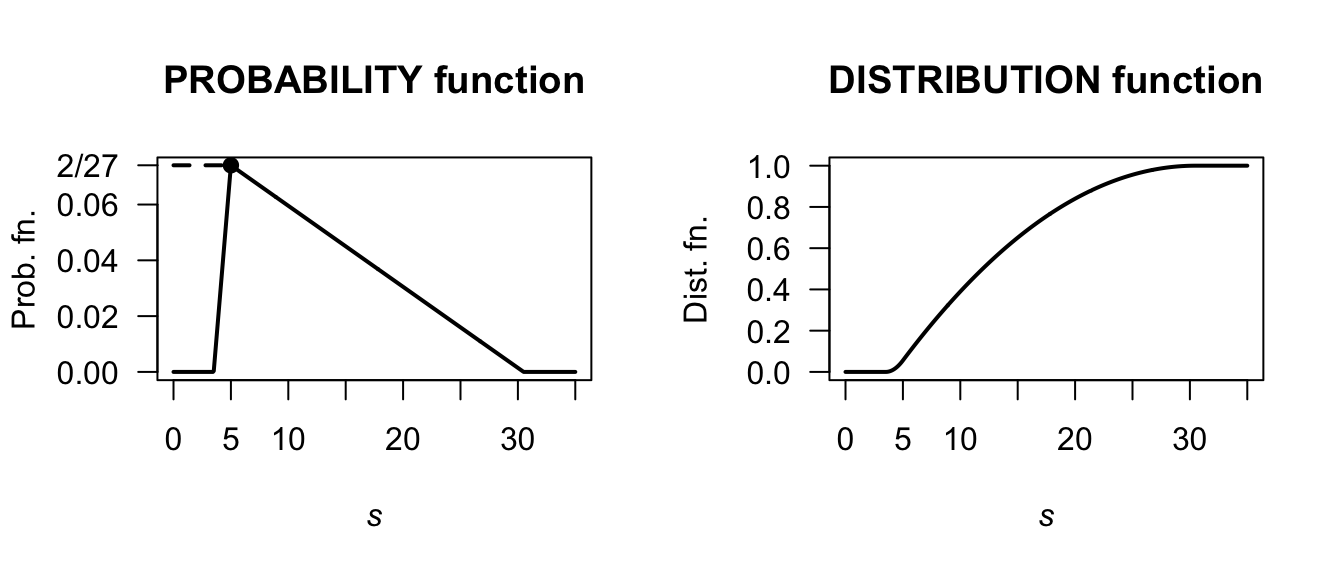
FIGURE E.8: A PDF and DF

(1 - Fx(20) ) / ( 1 - Fx(10))
#> [1] 0.2623443

Answer to Exercise 3.17.

Producers usually need that they will receive at least a certain amount of rainfall.
A very poor graph below; I really have to fix that.
Six months have recorded over $60\,\text{mm}$; so $6/81$. But taking half of the previous ‘40 to under 60’ category, we’d get $12/81$. So somewhere around there.
In June, there are $81$ observations, so the median is the $41st$: The median rainfall is between $0$ to under $20\,\text{mm}$. In December, there are $80$ observations, so the median is the $40.5$th: The median rainfall is between $0$ to under $60\,\text{mm}$.
Median; very skewed to the right.
…

#>       Buckets          Jun  Dec 
#>  [1,] "Zero"           "3"  "0" 
#>  [2,] "0 < R < 20"     "41" "17"
#>  [3,] "20 <= R < 40"   "19" "17"
#>  [4,] "40 <= R < 60"   "12" "21"
#>  [5,] "60 <= R < 80"   "2"  "9" 
#>  [6,] "80 <= R < 100"  "2"  "6" 
#>  [7,] "100 <= R < 120" "0"  "3" 
#>  [8,] "120 <= R < 140" "2"  "1" 
#>  [9,] "140 <= R < 160" "0"  "4" 
#> [10,] "160 <= R < 180" "0"  "0" 
#> [11,] "180 <= R < 200" "0"  "1" 
#> [12,] "200 <= R < 220" "0"  "1"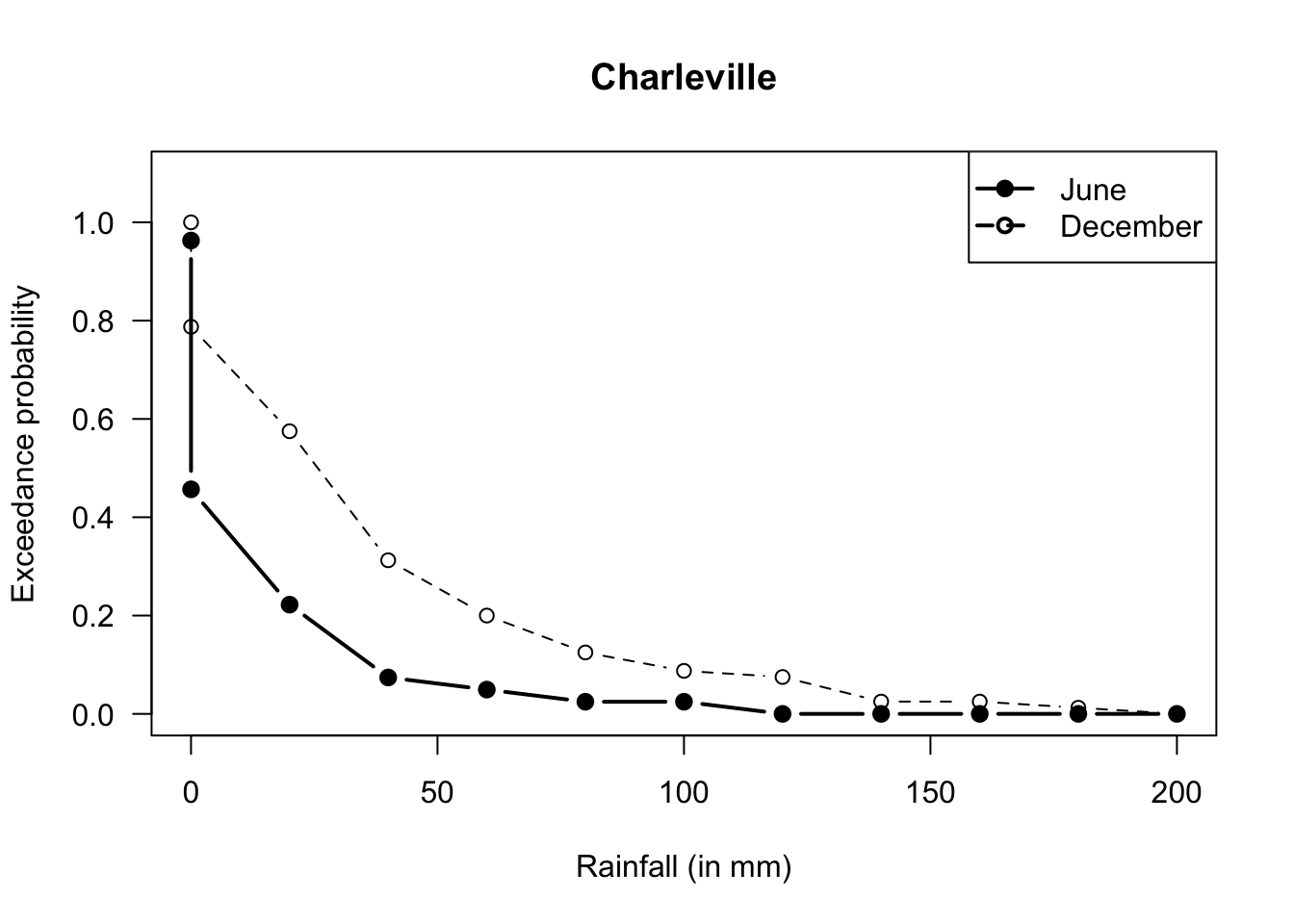

FIGURE E.9: Exceedance charts

Answer for Exercise 3.18.

Suppose I stand at Position 1; my friend can be at Positions 2 to 5, with distances $1$, $2$, $3$, $4$. Similar if I stand at Position 5.

Suppose I stand at Position 2; my friend can be at Positions 1, 3 to 5, with distances $1$, $1$, $2$, $3$. Similar if I stand at Position 4.

Suppose I stand at Position 3; my friend can be at Positions 1, 2, 4, 5, with distances $1$, $2$, $2$, $1$.

So counting, the PDF for the number of people between us, say $Y$, is: \[ f_Y(y) = \begin{cases} 4/10 & \text{for $y = 0$};\\ 3/10 & \text{for $y = 1$};\\ 2/10 & \text{for $y = 2$};\\ 1/10 & \text{for $y = 3$};\\ 0 & \text{elsewhere}. \end{cases} \] or $f_Y(y) = (4 - y)/10$ for $y\in\{0, 1, 2, 3\}$.

Answer for Exercise 3.19.

$a\int_0^1 (1 - y)^2\,dy = \left. (1 - y)^3/3\right|_0^1 = 1/3$.
$\Pr(|Y - 1/2| > 1/4) = \Pr(Y > 3/4) + \Pr(Y < 1/4) = 1 - \Pr(1/4 < Y < 3/4) = 13/32$.
See Fig. E.10.

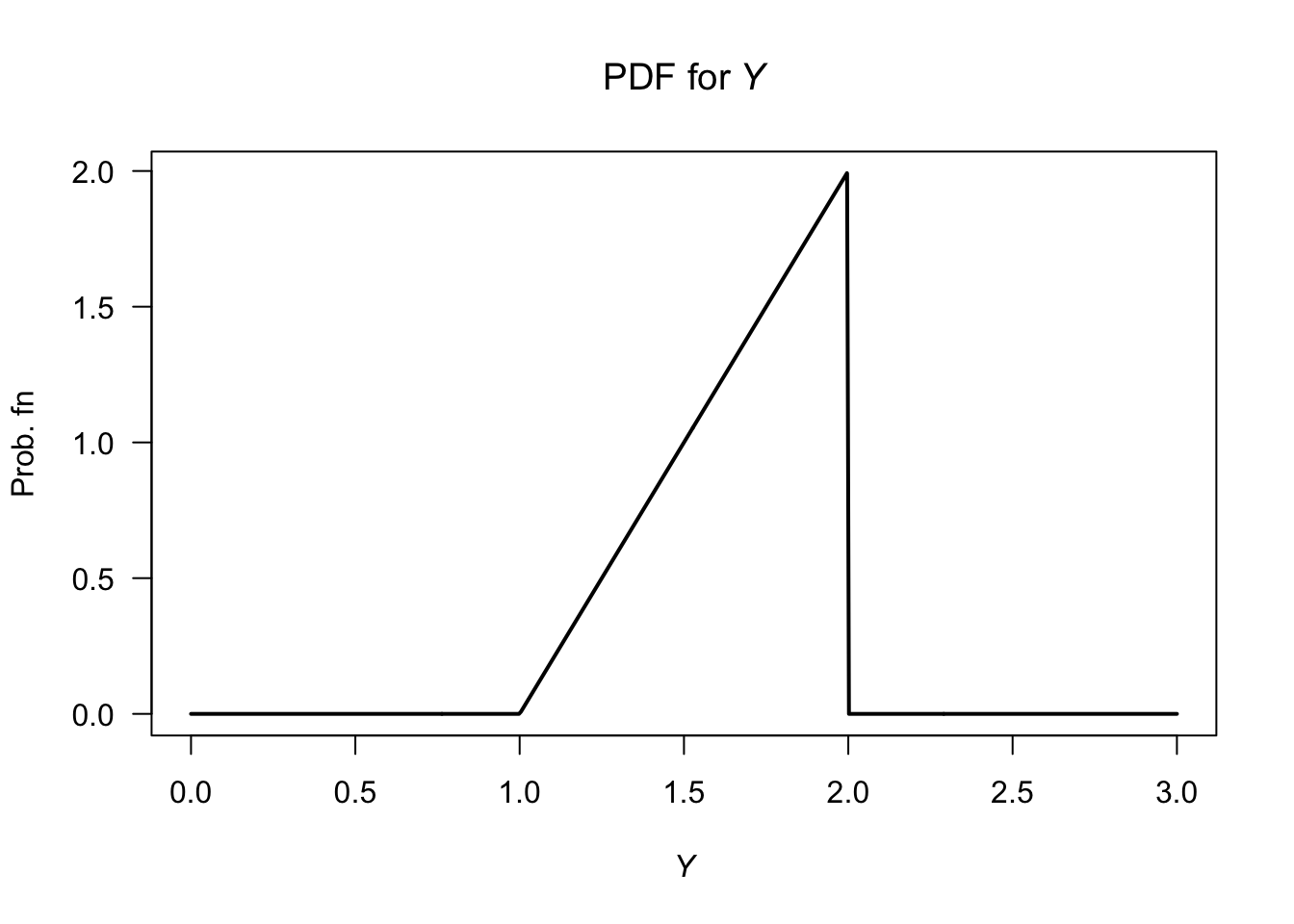
FIGURE E.10: The PDF of $y$

Answer for Exercise 3.20. df is: \[ F_Y(y) = \begin{cases} 0 & \text{for $y < 0$};\\ \frac{1}{3}(y - 1)^2 & \text{for $1 < y < 2$};\\ \frac{1}{3}(2y - 3) & \text{for $2 < y < 3$};\\ 1 & \text{for $y \ge 3$.} \end{cases} \] When $y = 3$, expect $F_Y(y) = 1$; this is true. When $y = 1$, expect $F_Y(y) = 0$; this is true. For all $y$, $0 \le F_Y(y) \le 1$.

Answer for Exercise 3.21. $\Pr(60 < Y < 70) = 154\,360\,000k/3\approx 51\,453\,333k$ and $\Pr(Y > 70) = 54\,360\,000k$. Using this model, the larger probability is dying over $70$.

Answer for Exercise 3.22. 1. See that $X = 1$ (i.e., one pooled test, and all are negative; no further testing needed) or $X = n + 1$ (the pooled test is positive, so $n$ individual tests are needed in addition to the pooled test). So the sample space is $\{1, n + 1\}$. 2. $X = 1$ only occurs if the test is negative; that is, $\Pr(X = 1) = (1 - p)^n$ So: \[ p_X(x) = \begin{cases} (1 - p)^n & \text{for $x = 1$ (i.e., the pooled test is negative)};\\ 1 - (1 - p)^n & \text{for $x = n + 1$} \end{cases} \] and zero elsewhere.

Answer for Exercise 3.23. We have cards like: \[ 2, 3, 4, \dots, 8, 9, 10, 10 (J), 10 (Q), 10 (K), 10 (A). \] That is, there are $20$ cards with a points value of ten (four suits of five cards each). For a ‘distance’ say $D$, of $8$, we need $\Pr[ (2, 10)\ \text{or}\ (10, 2)]$, with probability. \[ \Pr(D = 8) = 2\times \left(\frac{4 \times 20}{52 \times 51}\right). \] For a ‘distance’ of $7$, we need \[ \Pr[(3, 10)\ \text{or}\ (10, 3)] + \Pr[(2, 9)\ \text{or}\ (9, 2)], \] with probability \[ \Pr(D = 7) = 2\times\left(\frac{ \times 20}{52 \times 51}\right) + 2\times\left(\frac{4 \times 4}{52\times 51}\right). \] For a ‘distance’ of $6$, we need \[ \Pr[(4, 10)\ \text{or}\ (10, 4)] + \Pr[(3, 9)\ \text{or}\ (9, 3)] + \Pr[(2, 8)\ \text{or}\ (8, 2)] \] with probability \[ \Pr(D = 6) = 2\times\left(\frac{4 \times 20}{52 \times 51}\right) + 2\times\left(\frac{4 \times 4}{52\times 51}\right) + 2\times\left(\frac{4 \times 4}{52\times 51}\right). \] So in general, for $D = 1, 2, \dots 8$: \[ \Pr(D = d) = 2\times\left(\frac{4 \times 20}{52 \times 51}\right) + (8 - d)\times 2\times\left(\frac{4 \times 4}{52 \times 51}\right) \]

The case $D = 0$ is different. We can compute the probability as $1$ minus the probabilities from $D = 1$ to $D = 8$, or directly. By subtraction:

d <- 1:8
pd <- (2 * 4 * 20)/(52 * 51) + (8 - d) * (2 * 4 * 4)/(52 * 51)
rbind(d, pd)
#>         [,1]    [,2]      [,3]      [,4]
#> d  1.0000000 2.00000 3.0000000 4.0000000
#> pd 0.1447964 0.13273 0.1206637 0.1085973
#>          [,5]       [,6]       [,7]       [,8]
#> d  5.00000000 6.00000000 7.00000000 8.00000000
#> pd 0.09653092 0.08446456 0.07239819 0.06033183
1 - sum(pd)
#> [1] 0.1794872

To proceed directly, see that a ‘distance’ of zero can occur if we get a ‘ten’ and another ‘ten’, or a non-ten card plus the same non-ten card: \[ \Pr(D = 0) = \frac{20 \times 19}{52 \times 51} + \frac{32\times 3}{52\times 51}. \] The answer is the same:

(20 * 19)/(52 * 51) + (32 * 3)/(52 * 51)
#> [1] 0.1794872

See the PMF in Fig. E.11.

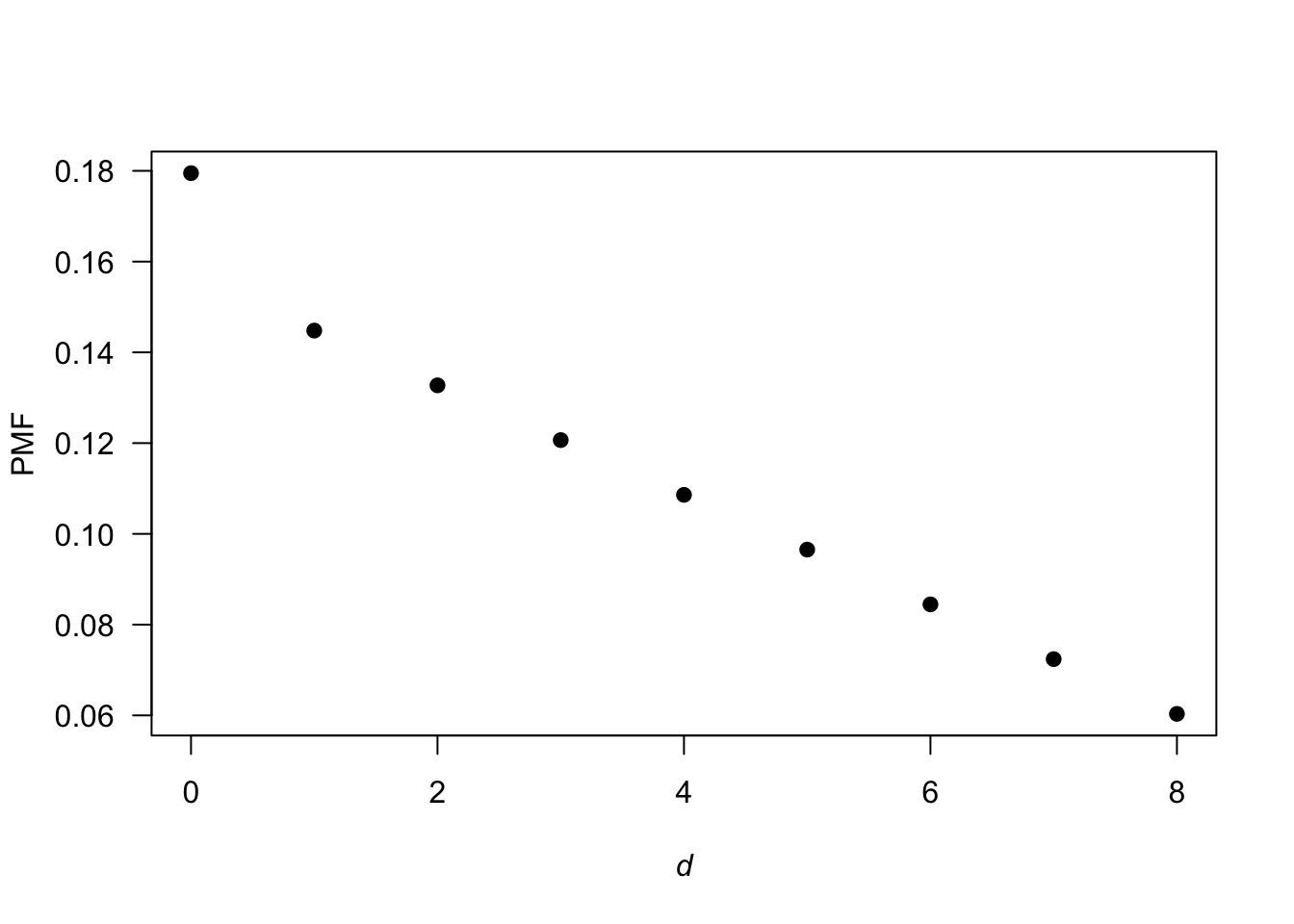
FIGURE E.11: The PDF for the `distance’ between cards

Answer for Exercise 3.24.

Write as $p(x) = \log_{10}(1 + x) - \log_{10}x$; then the sum is \[\begin{align*} (\log_{10}(2) - \log_{10} 1) + (\log_{10} 3 - \log_{10} 2) + (\log_{10} 4 - \log_{10} 3) + \dots\\ + (\log_{10} 9 - \log_{10} 8) + (\log_{10} 10 - \log_{10} 9) \end{align*}\] and things cancel, leaving $\log_{10}10 = 1$.
The df is \[\begin{align*} F_D(d) &= \sum_{i = 1}^d \log[ (1 + d)/ \log(d) ] \\ &= \sum_{i = 1}^d \log(1 + d) - \log d\\ &= (\log 2 - \log 1) + (\log 3 - \log 2) + \log 4 - \log 3) + \cdots\\ & \quad {} + (\log d - \log(d - 1) ) + (\log (1 + d) - \log d)\\ &= \log (1 + d). \end{align*}\]

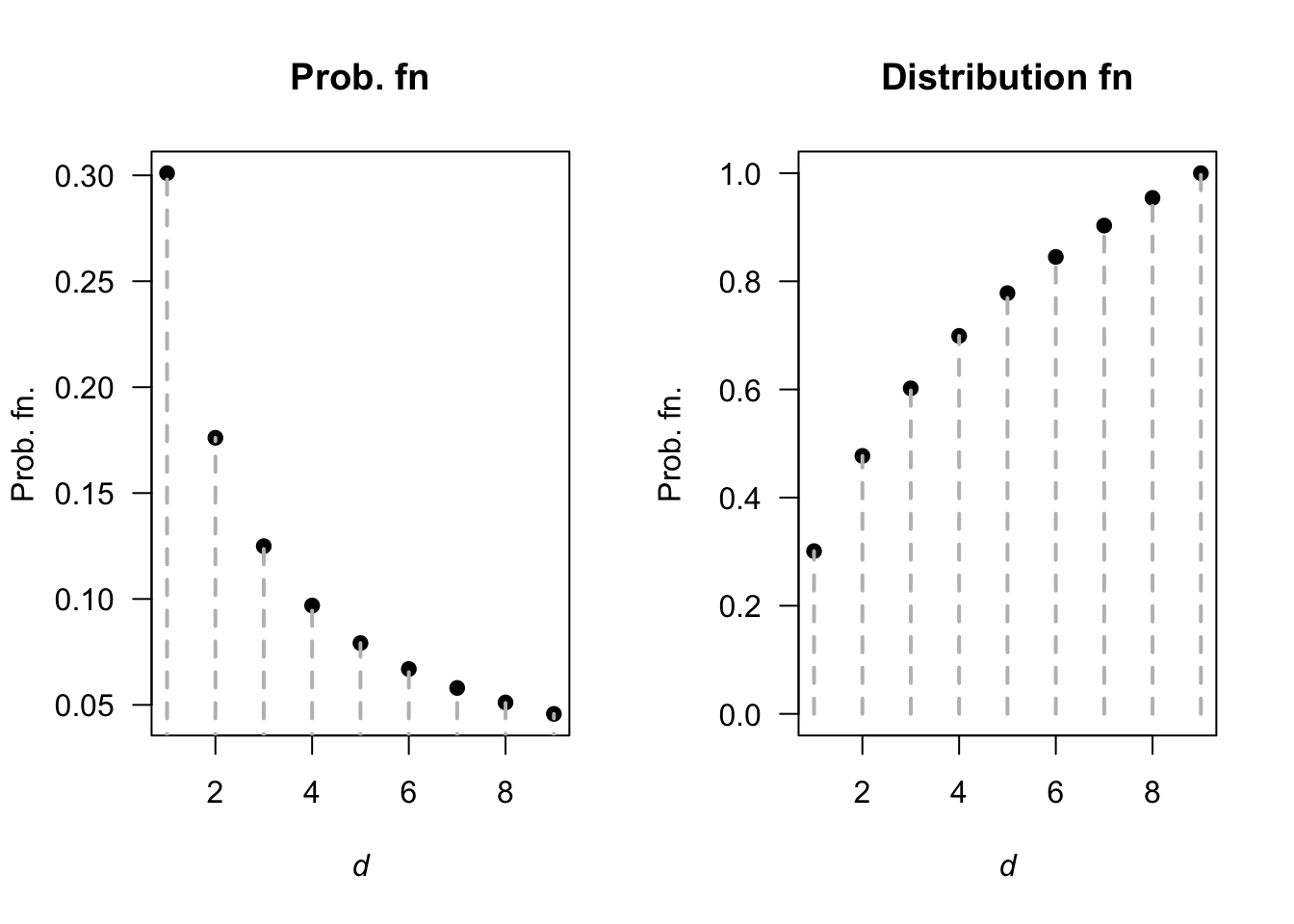
FIGURE E.12: A PDF and DF

Answer for Exercise 3.25.

$k = 1/\pi$. $F(y) = \int_0^x \frac{1}{\pi\sqrt{t(1 - t)}}\, dt = \frac{1}{\pi}\arcsin(2x - 1) + \frac{1}{2}$ for $0 < x < 1$. $\Pr(X > 0.25) = 2/3$.

#> Warning in sqrt(y * (1 - y)): NaNs produced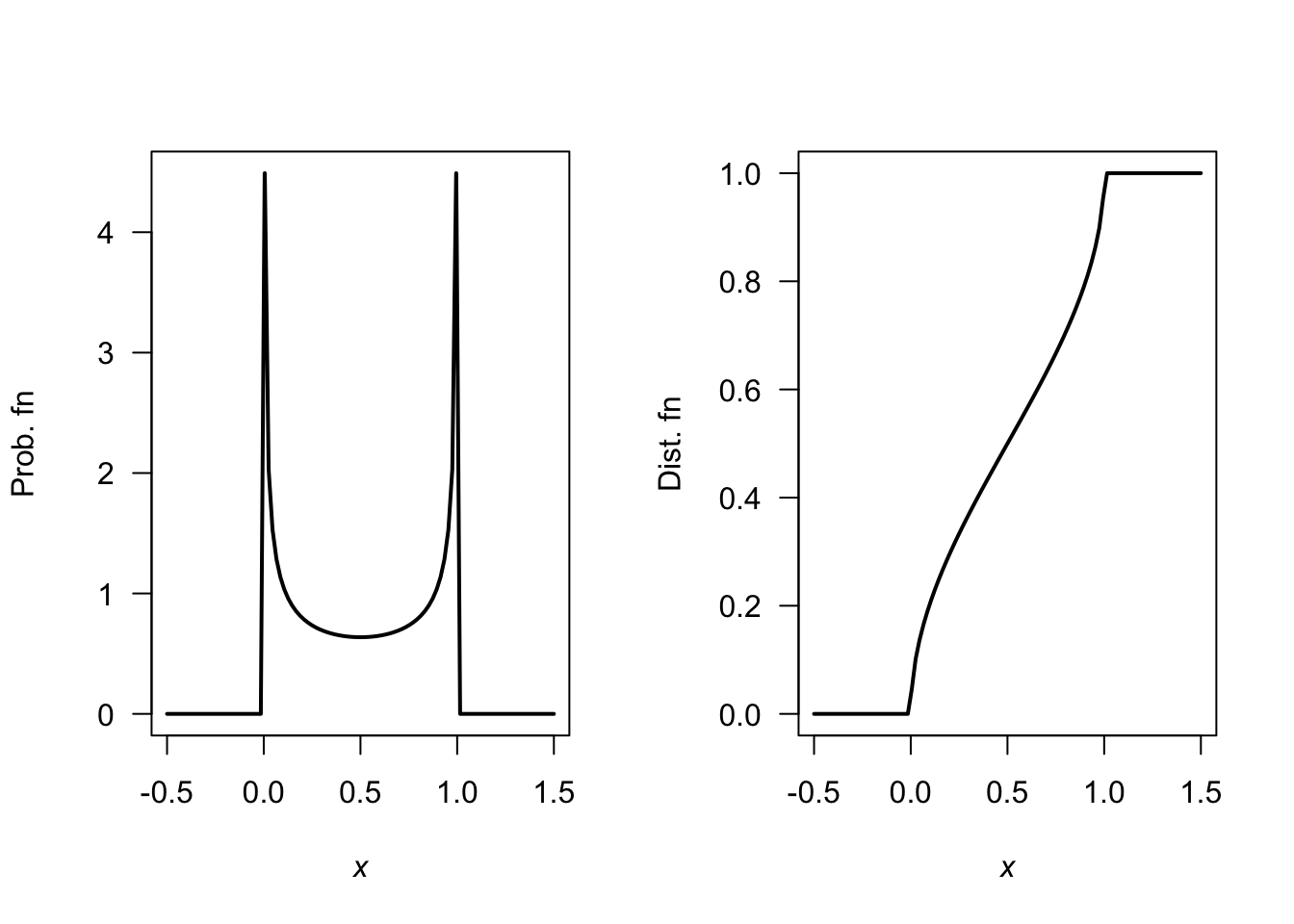

FIGURE E.13: A PDF and DF

Answer for Exercise 3.26.

The PDF is \[ f_X(x) = \frac{d}{dx} \exp(-1/x) = \frac{\exp(-1/x)}{x^2} \] for $x > 0$. See Fig. E.14.

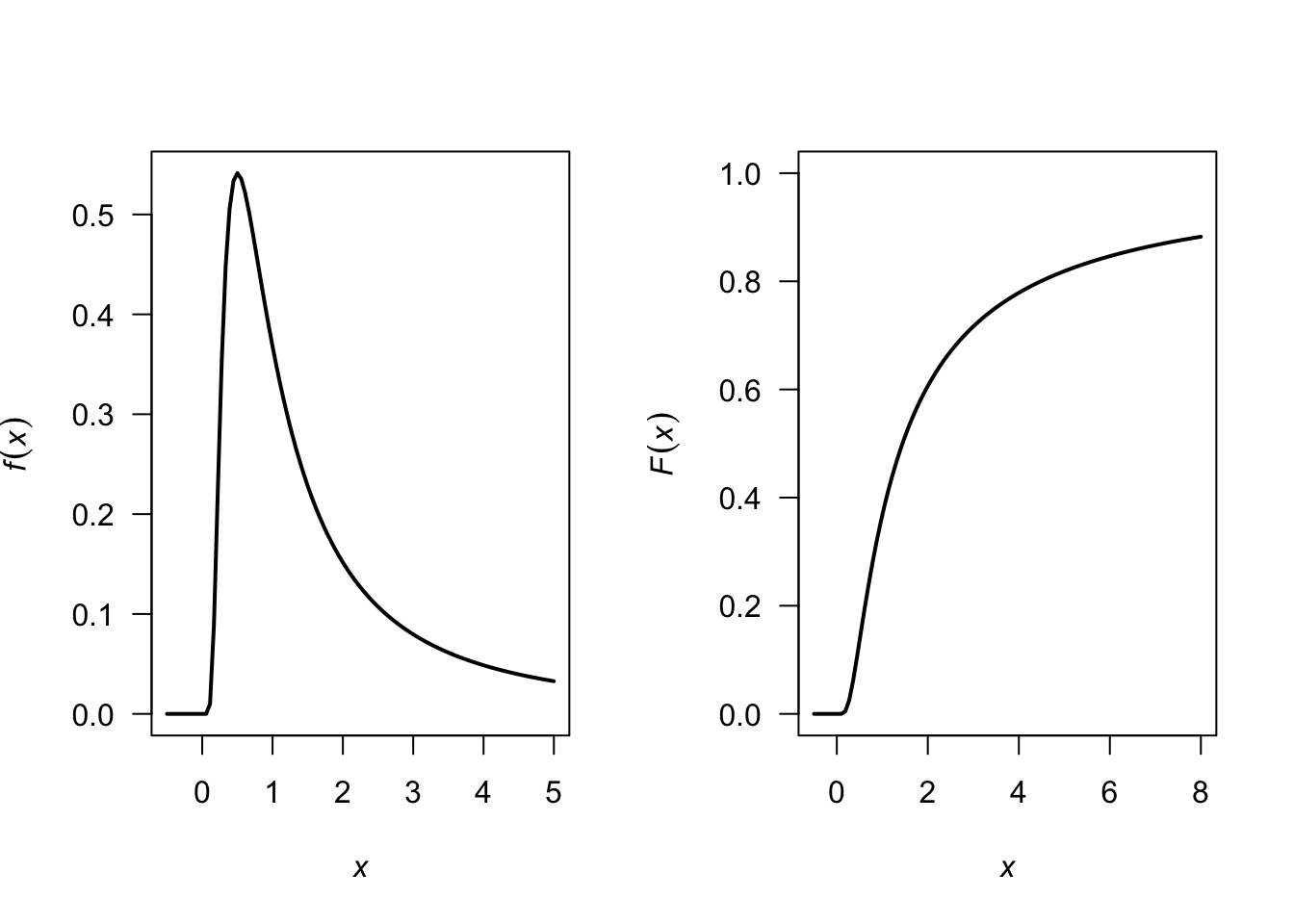
FIGURE E.14: A PDF

Answer for Exercise 3.27.

1 suit: Select 4 cards from the 13 of that suit, and there are four suits to select.
2 suits: There are two scenarios here:
- Three from one suit, and one from another: Choose a suit, and select three cards from it: $\binom{4}{3}\binom{13}{3}$. Then we need another suit (three choices remain) and one card from (any of the 13).
- Chose two suits, and two cards from each of two suits: $\binom{4}{2}\binom{13}{2}\binom{13}{2}$
3 suits: Umm…
4 suits: Choose one from each of the four suits.

One way to get 3 suits is to realise that the total probability must add to one…

### 1 SUIT
suits1 <- 4 * choose(13, 4) / choose(52, 4)

### 2 SUITS
suits2 <- choose(4, 3) * choose(13, 3) * choose(3, 1) * choose(13, 1) + 
          choose(4, 2) * choose(13, 2) * choose(13, 2)
suits2 <- suits2 / choose(52, 4)

### 4 SUITS:
suits4 <- choose(13, 1) * choose(13, 1) * choose(13, 1) * choose(13, 1)
suits4 <- suits4  / choose(52, 4)

suits3 <- 1 - suits1 - suits2 - suits4

round( c(suits1, suits2, suits3, suits4), 3)
#> [1] 0.011 0.300 0.584 0.105

Answer for Exercise 3.29. I have no idea…

From ChatGPT (i.e., haven’t checked):

At least four:

# Set the number of simulations
num_simulations <- 100000

# Initialize a vector to store the number of rolls required for each simulation
rolls_required <- numeric(num_simulations)

# Function to simulate rolling a die until the total is 4
simulate_rolls <- function() {
  total <- 0
  rolls <- 0
  while (total < 4) {
    roll <- sample(1:6, 1) # Roll the die
    total <- total + roll
    rolls <- rolls + 1
  }
  return(rolls)
}

# Perform simulations
for (i in 1:num_simulations) {
  rolls_required[i] <- simulate_rolls()
}

# Calculate the PMF
PMF <- table(rolls_required) / num_simulations

# Print the PMF
print(PMF)

# Optionally, plot the PMF
barplot(PMF, main="Probability Mass Function of Rolls Needed to Sum to 4",
        xlab="Number of Rolls", ylab="Probability",
        col="lightblue", border="blue")

Exactly four:

# Set the number of simulations
num_simulations <- 100000

# Initialize a vector to store the number of rolls required for each simulation
rolls_required <- integer(num_simulations)

# Function to simulate rolling a die until the total is exactly 4
simulate_rolls <- function() {
  total <- 0
  rolls <- 0
  while (total < 4) {
    roll <- sample(1:6, 1) # Roll the die
    total <- total + roll
    rolls <- rolls + 1
    if (total > 4) {
      return(NA) # Return NA if the total exceeds 4
    }
  }
  return(rolls)
}

# Perform simulations
for (i in 1:num_simulations) {
  result <- simulate_rolls()
  if (!is.na(result)) {
    rolls_required[i] <- result
  }
}

# Remove NA values from the results
rolls_required <- na.omit(rolls_required)

# Remove zero values (impossible cases)
rolls_required <- rolls_required[rolls_required > 0]

# Calculate the PMF
PMF <- table(rolls_required) / length(rolls_required)

# Print the PMF
print(PMF)

# Optionally, plot the PMF
barplot(PMF, main="Probability Mass Function of Rolls Needed to Sum to 4",
        xlab="Number of Rolls", ylab="Probability",
        col="lightblue", border="blue")

E.4 Answers for Chap. 4

Answer to Exercise 4.1.

This corresponds to the cell $X = 1, Y = 2$: $5/24\approx 0.208333$.
$\Pr(X + Y \le 1) = \Pr(X = 0, Y = 0) + \Pr(X = 0, Y = 1) + \Pr(X = 1, Y = 0) = 1/2$.
$\Pr(X > Y) = \Pr(X = 1, Y = 0) = 1/4$.
Write: \[ p_X(x) = \begin{cases} 7/24 & \text{if $x = 0$};\\ 17/24 & \text{if $x = 1$};\\ 0 & \text{otherwise}. \end{cases} \]
Only consider the column corresponding to $X = 1$: \[ p_{Y\mid X = 1}(y\mid x = 1) = \begin{cases} (1/4)/(17/24) = 6/17 & \text{if $y = 0$};\\ (1/4)/(17/24) = 6/17 & \text{if $y = 1$};\\ (5/24)/(17/24) = 5/17 & \text{if $y = 2$};\\ 0 & \text{otherwise}. \end{cases} \]

Answer to Exercise 4.2.

$0$.
$9/15$.
$\Pr(Y = 0) = 1/15$; $\Pr(Y = 1) = 6/15$; $\Pr(Y = 2) = 4/15$; $\Pr(Y = 3) = 3/15$; $\Pr(Y = 4) = 1/15$.
$\Pr(X = 1) = 4/15$; $\Pr(X = 2) = 5/15$; $\Pr(X = 3) = 6/15$.
$\Pr(Y = 1\mid X = 1) = 2/4$; $\Pr(Y = 2\mid X = 1) = 1/4$; $\Pr(Y = 3\mid X = 1) = 1/4$.

Answer to Exercise 4.3. 1. $\int_0^2\!\!\!\int_0^1 x + y^2\, dy\, dx = 11/3$, so $k = 3/11$. 2. $\dfrac{3}{11} \int_1^2\!\!\!\int_{1/2}^1 x + y^2\, dy\, dx = 37/88\approx 0.42045$. 3. ??? 4. $\dfrac{3}{11} \int_0^2 x + y^2\, dy = 2(3x + 4)/11$ for $0 < x < 1$. 5. $\dfrac{3}{11} \int_0^1 x + y^2\, dx = 3(2y^2 + 1)/22$ for $0 < y < 2$. 6. $2(x + y^2) / [2(3x + 4)]$ for $0 < x < 1$, $0 < y < 2$. 7. $3(1 + y^2) / 14$ for $0 < y < 2$. 8. $2(x + y^2) / (2y^2 + 1)$ for $0 < x < 1$, $0 < y < 2$. 9. $2(x + 1)/3$ for $0 < x < 1$. 10. No.

Answer to Exercise 4.4. 1. $k = 1/7$. 2. $3/7\approx 9.42857$$. 3. ??? 4. $2(x + 2)/7$ for $1 < x < 2$. 5. $(7 - 2y)/14$ for $-1 < y < 1$ for $1 < x < 2$, $-1 < y < 1$. 6. $(2 + x - y)/[(2(x + 2)]$ for $1 < x < 2$, $-1 < y < 1$. 7. $(3 - y)/6$ for $-1 < y < 1$. 8. $2(2 + x -y)/(7 - 2y)$ for $1 < x < 2$. 9. $2(2 + x)/7$ for $1 < x < 2$. 10. No.

Answer to Exercise 4.8.

Need integral to be one: $\displaystyle \int_0^1\!\!\!\int_0^1 kxy\, dx\, dy = 1$, so $k = 4$.
Here: \[ 4 \int_0^{3/8}\!\!\!\int_0^{5/8} kxy\, dx\, dy = 225/4096\approx 0.05493. \]

Answer to Exercise 4.10.

Construct table (below) from listing all four outcomes.
We get \[ p_X(x) = \begin{cases} 1/4 & \text{for $x = 0$};\\ 1/2 & \text{for $x = 1$};\\ 1/4 & \text{for $x = 2$}. \end{cases} \]
When given $Y = 1$, then the probability function is non-zero for $x = 1, 2$: \[ p_{X\mid Y = 1}(x \mid Y = 1) = \begin{cases} 1/2 & \text{for $x = 1$};\\ 1/2 & \text{for $x = 2$}; \end{cases} \]
Not independent; for instance, when $Y = 0$, $\Pr(X) > 0$ for $x = 0, 1$, in constrast to when $Y = 1$.

.	$X = 0$	$X = 1$	$X = 2$
$Y = 0$	$1/4$	$1/4$	$0$
$Y = 1$	$0$	$1/4$	$1/4$

Answer to Exercise 4.11. The joint probability function for $X$ and $Y$ is shown in Table E.2. For example:

A minimum of 2 and a maximum of 1 is impossible; this makes no sense (hence probability is zero).
A minimum of 3 and a maximum of 4 can happen in two ways: a 4 on the first die and a 3 on the other, or a 3 on the first die and a 4 on the other.
A minimum and a maximum of 2 can only happen one way: both dice show a 2.

The joint distribution for $C$ and $D$ is therefore:

	$C = 0$	$C = 1$
$D = 0$	$6/36$	$6/36$
$D = 1$	$12/36$	$12/36$

Then, the marginal distribution for $B$ (the minimum) is \[ f_B(b) = \begin{cases} 11/36 & \text{for $b = 1$};\\ 9/36 & \text{for $b = 2$};\\ 7/36 & \text{for $b = 3$};\\ 5/36 & \text{for $b = 4$};\\ 3/36 & \text{for $b = 5$};\\ 1/36 & \text{for $b = 6$} \end{cases} \] which is easily confirmed as a valid PMF.

TABLE E.2: The minimum and maximum from two rolls of a die
	$\text{min} = 1$	$\text{min} = 2$	$\text{min} = 3$	$\text{min} = 4$	$\text{min} = 5$	$\text{min} = 6$
$\text{max} = 1$	1/36	0/36	0/36	0/36	0/36	0/36
$\text{max} = 2$	2/36	1/36	0/36	0/36	0/36	0/36
$\text{max} = 3$	2/36	2/36	1/36	0/36	0/36	0/36
$\text{max} = 4$	2/36	2/36	2/36	1/36	0/36	0/36
$\text{max} = 5$	2/36	2/36	2/36	2/36	1/36	0/36
$\text{max} = 6$	2/36	2/36	2/36	2/36	2/36	1/36

Answer to Exercise 4.12.

See Fig. E.15.
Integrate correctly! $\displaystyle \int_0^2 \!\!\!\int_0^{2 - x} x(y + 1)\,dy \, dx = 2$, so $c = 1/2$.
$P(Y < 1 \mid X > 1) = P(Y < 1 \cap X > 1)/\Pr(X > 1)$. First, $f_X(x) = (1/2) \int_0^{2 - x} x(y + 1)\,dy = (1/4)(x^3 - 6x^2 + 8x)$ for $0 < x < 2$. So $\Pr(X > 1) = 7/16 = 0.4375$. Also, \[ P(Y < 1 \cap X > 1) = (1/2) \int_1^2 \!\!\!\int_0^{2 - x} x(y + 1)\,dy \, dx = 7/16. \] Then, $P(Y < 1 \mid X > 1) = 1$, which makes sense from the diagram (if $X > 1$, $Y$ must be less than 1).
$P(Y < 1 \mid X > 0.25) = P(Y < 1 \cap X > 0.25)/\Pr(X > 0.25)$. Using results from above, $\Pr(X > 0.25) = 3871/4096 = 0.945068$ and $P(Y < 1 \cap X > 0.25) = 0.945$. So $P(Y < 1 \mid X > 0.25) = P(Y < 1 \cap X > 0.25)/\Pr(X > 0.25)$.
First, $f_Y(y) = \frac{1}{2} \int_0^{2 - y} x(y + 1)\, dx = \frac{1}{4}(y + 1)(y - 2)^2$. Then, \[ \Pr(Y < 1) = \int_0^1 \frac{1}{4}(y + 1)(y - 2)^2\, dy = \frac{13}{16}\approx 0.8125. \]

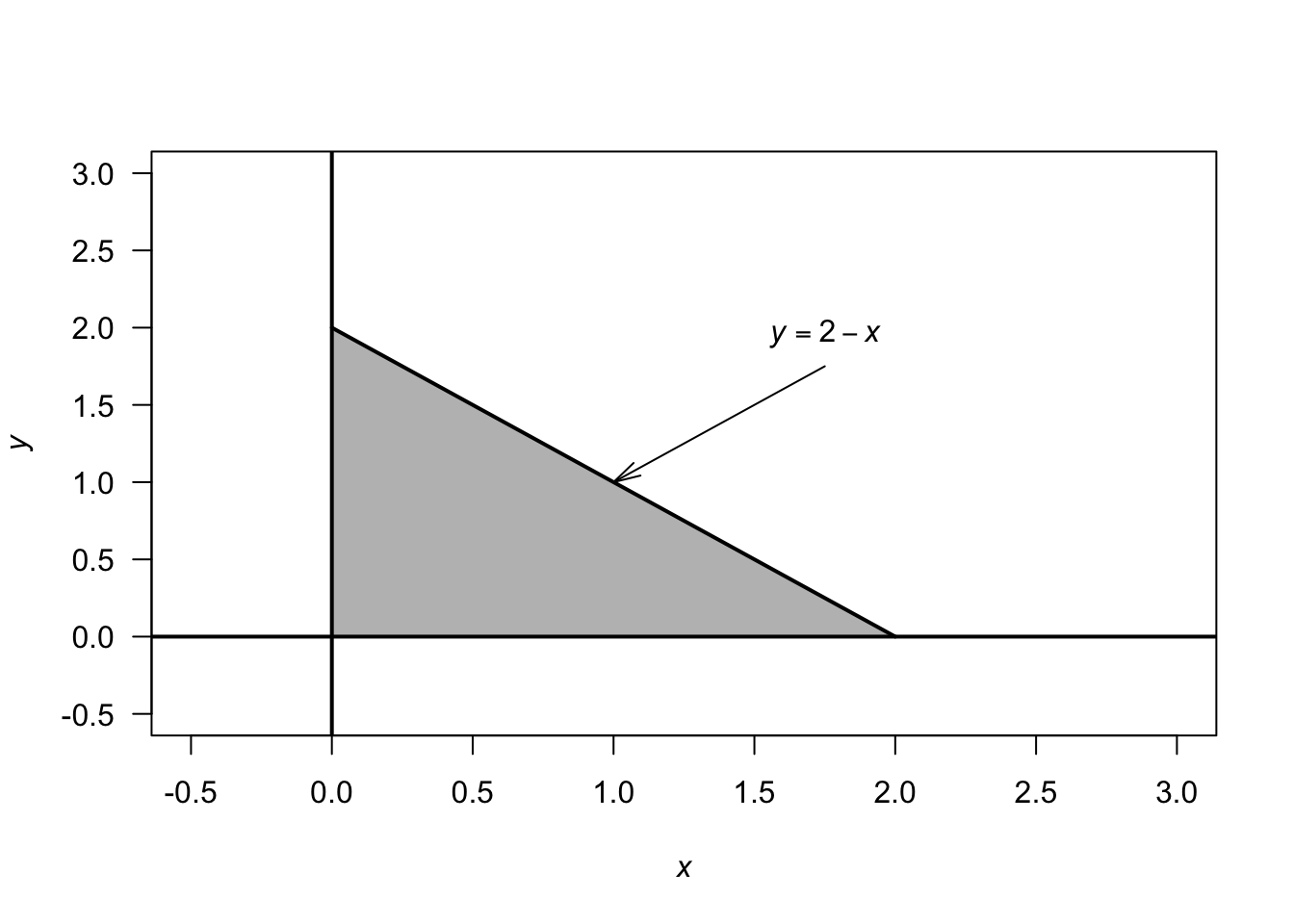
FIGURE E.15: The region where $X$ and $Y$ have positive probability

Answer to Exercise 4.13.

Proceed: \[\begin{align*} 1 &= k\int_0^1\!\!\!\int_0^{\sqrt{y}} (1 - x)y\, dx\, dy\\ &= k\int_0^1\!\!\!\int_{x^2}^{1} (1 - x)y\, dy\, dx\\ &= \frac{k}{2}\int_0^1 (1 - x) (1 - x^4) \, dx\\ &= \frac{7k}{30}, \end{align*}\] so that $k = 30/7\approx 4.285714$.
Being careful with the integration limits again (draw a diagram!): \[\begin{align*} \Pr(X > Y) &= \int_0^1 \!\int_y^{\sqrt{y}} f(x, y)\, dx\, dy\\ &= \int_0^1 \!\int_x^{x^2} f(x, y)\, dy\, dx\\ &= \frac{15}{7} \int_0^1 (x - 1) x^2 (x^2 - 1)\, dx\\ &= 3/28\approx 0.1071429. \end{align*}\]
First find the marginal distribution of $X$: \[ f_X(x) = \int_{x^2}^1 f(x, y)\, dy = \frac{15}{7} (x - 1)(x^4 - 1), \] and so \[ \Pr(X > 0.5) = \frac{15}{7} \int_{1/2}^1 (x - 1)(x^4 - 1)\, dx = \frac{183}{896}\approx 0.2042411. \]

E.5 Answers for Chap. 5

Answer for Exercise 5.1.

$k = -2$.
See Fig. E.16.
$\operatorname{E}(Y) = 5/3$.
$\operatorname{E}(Y^2) = 17/6$, so $\text{var(Y)} = 17/6 - (5/3)^2 = 1/18$.
$\Pr(X > 1.5) = \int_{1.5}^2 f_Y(y)\, dy = 3/4$.

FIGURE E.16: The PDF for Y

Answer to Exercise 5.2. 1. Plot not shown. 2. $1/3$. 3. $7/18$. 4. $2/3$.

Answer to Exercise 5.5.

First: $k = 1/4$.

Plot not shown.
$\operatorname{E}(D) = 7/4 = 1.75$; $\operatorname{E}(D^2) = 15/4$ so $\operatorname{var}(D) = 11/16 = 0.6875$.
$M_D(t) = \exp(t)/2 + \exp(2t)/4 + \exp(3t)/4$.
Mean and variance as above.
$\Pr(D < 3) = 3/4$.

Answer to Exercise 5.6. First, $c = 144/205$.

Plot not shown.
$\operatorname{E}(D) = 60/41\approx 1.46\dots$; $\operatorname{var}(D) = 5616/8405\approx 0.668\dots$.
$M_Z(t) = \frac{\exp(t)}{205}(36\exp(t) + 16\exp(2t) + 9\exp(3t) + 144)$.
Mean and variance as above.
$61/205$.

Answer to Exercise 5.7.

$M_Z'(t) = 0.6\exp(t)[0.3\exp(t) + 0.7]$ so $\operatorname{E}(Z) = 0.6$. Also, $M''_Z(t) = 0.18\exp(2t) + 0.6\exp(t)[0.3\exp(t) + 0.7]$ so $\operatorname{E}(Z^2) = 0.78$, so $\operatorname{var}(Z) = 0.42$ (be careful with the derivatives here!)
Expand the quadratic and find: $\Pr(Z = 0) = 0.49$, $\Pr(Z = 1) = 0.42$, $\Pr(Z = 2) = 0.09$.

Answer to Exercise 5.8.

$\operatorname{E}[W] = (1 - p)/p$; $\operatorname{var}[W] = (1 - p)/p^2$.
$p_W(w) = (1 - p)^x$ for $x = 1, 2, \dots$.

Answer to Exercise 5.10.

$17$.
$5 + 2 + 0.2 = 7.2$.
$14$.
$(2^2\times 5) + ((-3)^2\times 2) + (2\times -3\times 0.2) = 36.8$.

Answer to Exercise 5.14. $[exp(tb) - \exp(ta)]/[t (b - a)]$ for $t\ne 0$.

Answer to Exercise 5.11.

$M'_G(t) = \alpha\beta(1 - \beta t)^{-\alpha - 1}$ so $\operatorname{E}(G) = \alpha\beta$. $M''_G(t) = \alpha\beta^2(\alpha + 1)(1 - \beta t)^{-\alpha - 2}$ so $\operatorname{E}(G^2) = \alpha\beta^2(\alpha + 1)$ and $\operatorname{var}(G) = \alpha\beta^2$.

Answer to Exercise 5.12.

Proceed: \[ \mu'_r = \operatorname{E}(X^r) = \int_{x = 0}^1 x^r 2(1 - x)\, dx = 2\left[ \left(\frac{x^{r + 1}}{r + 1} - \frac{x^{r + 2}}{r + 2}\right)\Big|_{0}^{1}\right] = 2\left[ \frac{1}{r + 1} - \frac{1}{r + 2}\right]. \]
Expanding, $\operatorname{E}((X + 3)^2) = \operatorname{E}(X^2) + 6\operatorname{E}(X) + 9$. Now, $\operatorname{E}(X) = \mu'_1 = 1/3$ from above, and $\operatorname{E}(X^2) = \mu'_2 = 1/6$ from above. Hence $\operatorname{E}((X + 3)^2) = 67/6$.
$\operatorname{var}(X) = \operatorname{E}(X^2) - \operatorname{E}(X)^2 = 1/18$.

Answer to Exercise 5.9.

$13 + 4 = 17$.
$5 + 2 = 7$.
$(2\times 13) - (3\times 4) = 14$.
$(2^2\times 5) + (-3)^2\times 2) = 38$.

Answer to Exercise 5.15. $\left[6\left( (t - 2)\exp(t) + t + 2\right)\right]/t^3$ for $t\ne 0$.

Answer to Exercise 5.16.

$\operatorname{E}(Y) = \int_2^\infty y\frac{2}{y^2}\,dy = 2\log y\Big|_2^\infty$, which does not converge.
If $\operatorname{E}(Y)$ is not defined, then $\operatorname{var}(Y)$ cannot be defined either.
See Fig. E.17, left panel.
$F_Y(y) = \int_2^y 2/t^2\, dt = 1 - (2/y)$; see Fig. E.17, right panel.
$F_Y(y) = 0.5$ gives the median as $4$.
$F_Y(y) = 1/4$ gives $Q_1 = 8/3$; $F_Y(y) = 3/4$ gives $Q_3 = 8$; so IQR is $8 - 8/3 = 16/3$.
$\Pr(Y > 4\mid Y > 3) = \Pr(Y > 4)/\Pr(Y > 3)$. Then, $\Pr(Y > 4) = 1 - \Pr(Y < 4) = 1/2$ using the df; and $\Pr(Y > 3) = 1 - \Pr(Y < 3) = 2/3$ using the df; so the answer is $3/4$.

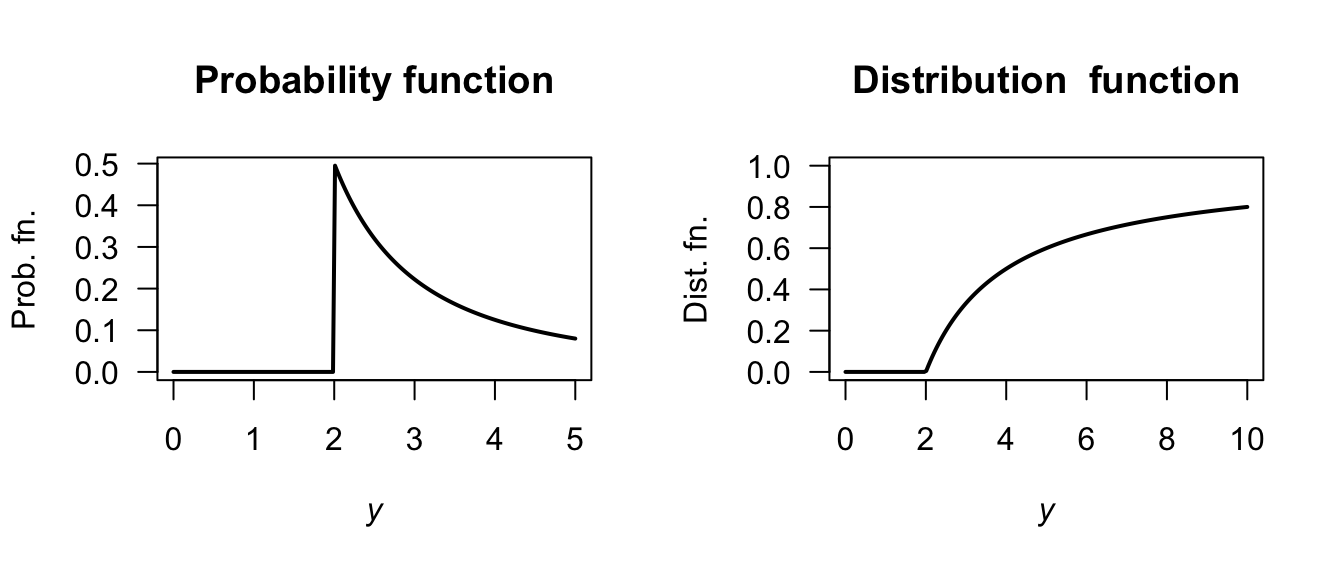
FIGURE E.17: The probability and distribution functions for a distribution with no mean

Answer to Exercise 5.17.

See Fig. E.18 (left panel).
Evaluate $F_X(t) = \displaystyle \int_{-\infty}^t \frac{1}{\pi(1 + x^2)}\,dx = \frac{1}{\pi}\arctan(x) + \frac{1}{2}$. See Fig. E.18 (right panel).
$\displaystyle \operatorname{E}(X) = \int_{-\infty}^t \frac{x}{\pi(1 + x^2)}\,dx = ...$, which is not defined.

FIGURE E.18: The Cauchy distribution

Answer to Exercise 5.19.

Begin with Definition 5.10 for $M_X(t)$ and use fact that if a distribution is symmetric about $0$ then $f_X(x) = f_X(-x)$ using symmetry. Transform the resulting integral.

Answer to Exercise 5.20. 1. Any real $a$ satisfies the conditions. 2. Need $a = -1$.

Answer to Exercise 5.21.

On solving, find $a = 1$ or $a = 1/2$.
For $a = 1$, $\operatorname{E}[X] = 1/2$. For $a = 1/2$, $\operatorname{E}[X] = 31/60 > 1/2$, so $a = 1/2$.

Answer to Exercise 5.22.

First, the PDF needs to be defined (see Fig. E.19), and define $W$ as the waiting time. Let $H$ be the ‘height’ of the triangle. The area of triangle $A_1$ is $3H/4$, and the area of triangle $A_2$ is $51H/4$, so $H = 2/27$.

The two lines, $L_1$ and $L_2$ can be found (find the slope; determine the linear equation) so that: \[ f_W(w) = \begin{cases} 4w/81 - 14/81 & \text{for $3.5 < w < 5$};\\ -4w/1377 + 122/1377 & \text{for $5 \le w < 30.5$}. \end{cases} \]

$\operatorname{E}(W)$ can be computed as usual across the two parts of the PDF: $\operatorname{E}(W) = \frac{1}{4} + \frac{51}{4} = 13$ minutes.
$\operatorname{E}(W^2)$ can be computed in two parts also: $\operatorname{E}(W^2) = \frac{163}{144} + \frac{29\,699}{144} = 16598/8$. Hence $\operatorname{var}(Y) = (1659/8) - 13^2 = 307/8\approx 38.375$, so the standard deviation is $\sqrt{38.375} = 6.19$ minutes.

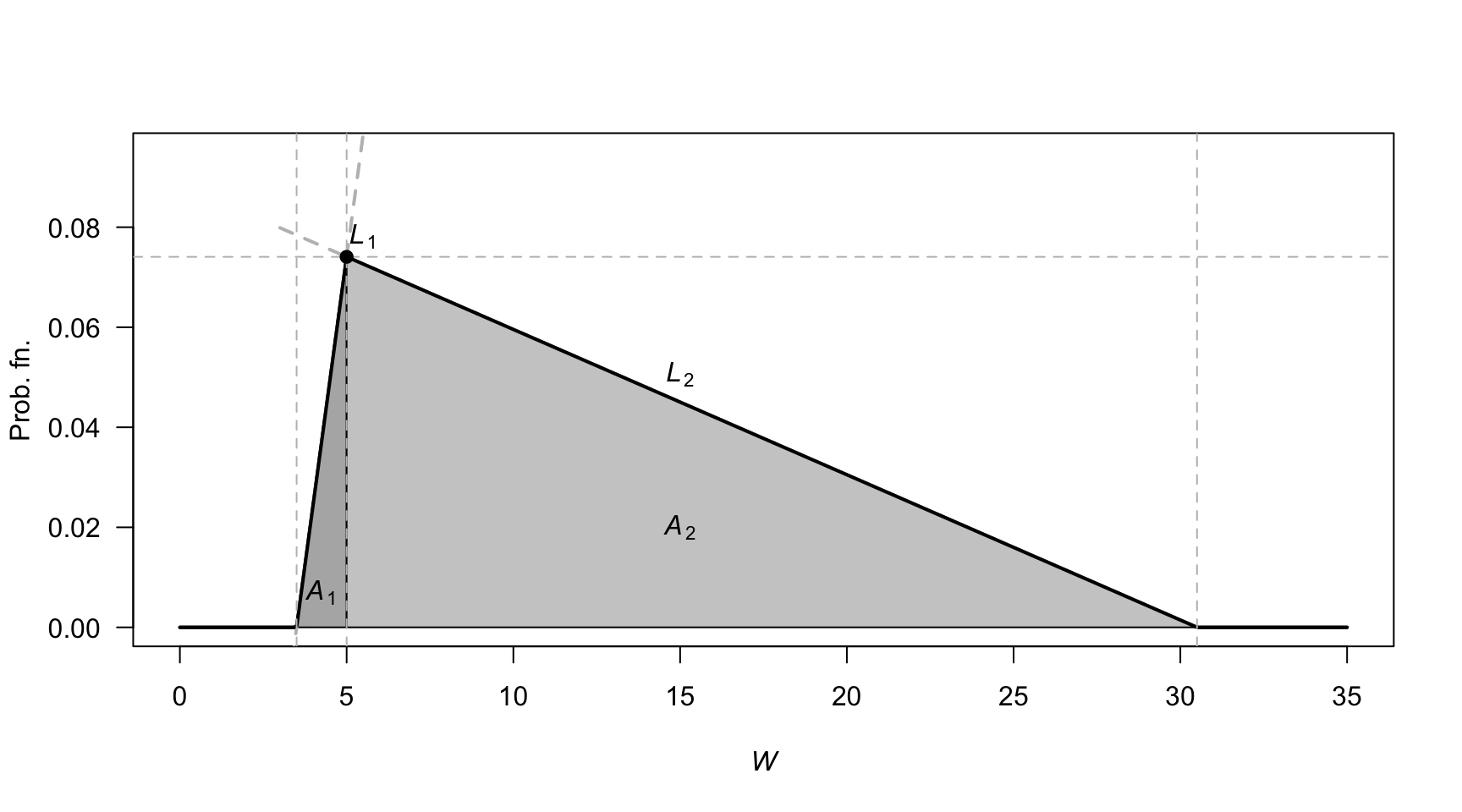
FIGURE E.19: Waiting times

Answer for Exercise 5.23.

Using the PMF from Exercise 3.18: \[ \operatorname{E}(X) = \left(0\times\frac{4}{10}\right) + \left(1\times\frac{3}{10}\right) + \left(2\times\frac{2}{10}\right) + \left(3\times\frac{1}{10}\right) = 1. \] In R:

set.seed(777023)

dist <- array(NA, dim = 1000)
for (i in (1:1000)){
  positions <- sample(1:5,
                      size = 2,
                      replace = FALSE)
  dist[i] = abs(diff(positions)) - 1
}
mean(dist)
#> [1] 0.926

Answer to Exercise 5.24. 1. Show by substituting. 2. Proceed: \[ \varphi(t) = \operatorname{E}[\exp(itX)]\\ = \int_{\mathbb{R}} \exp(itx) f(x)\, dx. \] Differentiating wrt $t$: \[ \varphi(t)' = \int_{\mathbb{R}} ix \exp(itx) f(x)\, dx. \] Setting $t = 0$: \[ \varphi(0)' = \int_{\mathbb{R}} xi f(x)\, dx, \] and so $-i\varphi(0) = \operatorname{E}[X]$ as to be shown.

Answer to Exercise 5.25.

$(1 - a)^{-1} = 1 + a + a^2 + a^3 + \dots = \sum_{n=0}^\infty a^n$ for $|a| < 1$.
$(1 - tX)^{-1} = 1 + tX + t^2X^2 + t^3X^3 + \dots = \sum_{n=0}^\infty t^n X^n$ for $|tX| < 1$. Thus: \[\begin{align*} \operatorname{E}\left[ (1 - tX)^{-1}\right] &= \operatorname{E}[1] + \operatorname{E}[tX] + \operatorname{E}[t^2X^2] + \operatorname{E}[t^3X^3] + \dots\\ &= \sum_{n=0}^\infty \operatorname{E}\left[ t^n X^n\right] \quad \text{for $|tX| < 1$}. \end{align*}\]
Using the definition of an expected value: \[\begin{align*} R_Y(t) &= \operatorname{E}\left[ (1 - tY)^{-1} \right]\\ &= \int_0^1 \frac{1}{1 - ty}\, dy = -\frac{\log(1 - t)}{t}. \end{align*}\]
Using the series expansion of $\log(1 - t)$: \[ \log(1 - t) = -t - \frac{t^2}{2} - \frac{t^3}{3} + \dots \] and so \[ -\frac{\log(1 - t)}{t} = 1 + \frac{t}{2} + \frac{t^2}{3} + \dots. \]
Equating this expression with that found in Part 2: \[\begin{align*} 1 + \frac{t}{2} + \frac{t^2}{3} + \dots. &= 1 + \operatorname{E}[tY] + \operatorname{E}[t^2 Y^2] + \operatorname{E}[t^3 Y^3] + \dots\\ &= 1 + t \operatorname{E}[Y] + t^2\operatorname{E}[Y^2] + t^3\operatorname{E}[Y^3] + \dots \end{align*}\] and so \[\begin{align*} t \operatorname{E}[Y] &= t/2 \Rightarrow \operatorname{E}[Y] = 1/2;\\ t^2 \operatorname{E}[Y^2] &= t^2/3 \Rightarrow \operatorname{E}[Y^2] = 1/3;\\ t^n \operatorname{E}[Y^n] &= t^n/(n + 1) \Rightarrow \operatorname{E}[Y^n] = 1/(n + 1).\\ \end{align*}\]

Answer to Exercise 5.26. First see that the area under the curve must be one, so \[ 1 = \int_{-c}^c k(3x^2 + 4)\, dx = k(2c^3 + 8c). \] Then, note that $\operatorname{E}(W) = 0$ (as the PDF is symmetric about 0), so that $\operatorname{var}(X) = \operatorname{E}(X^2)$, and: \[ \operatorname{E}(X^2) = \int_{-c}^c k x^2 (3x^2 + 4)\, dx = k c^3\frac{18c^2 + 40}{15} = \frac{28}{15}, \] and hence, equating the top lines of both fractions: \[ k c^3(9c^2 + 20) = 14. \] So we have two equations in two unknowns. Equating we obtain, after some algebra, \[ 9 c^4 - 8c^2 - 112 = 0. \] This is just a quadratic equation in $c^2$; so write \[ 9 X^2 - 8X - 112 = (9X + 28)(X - 4) = 0 \] with the two solutions $X = c^2 = -28/9$ (which has no real solutions for $c$), and $X = c^2 = 4$, so that $c = 2$ (as the PDF must be positive), giving $k = 1/32$.

Answer to Exercise 5.27. 1. $c = 1 - 3k/2$ and $c > 0$ and $k > 0$. 2. $c = k = 2/5$. 3. Not possible.

Answer to Exercise 5.28. $k = \infty$.

Answer to Exercise 5.29. $r = 5$.

Answer to Exercise 5.30. $\operatorname{E}[D] = \sum_{d=1}^9 \log_{10}\left(\frac{d + 1}{d}\right) \times d$. By expanding, and collecting like terms, and simplifying (e.g., $\log_{10} 1 = 0$ and $\log_{10}10 = 1$), find \[ \operatorname{E}[D] = -\log_{10}2 - \log_{10}3 - \cdots - \log_{10}8 - \log_{10}9 + 9 \approx 3.440. \]

Answer to Exercise 5.31.

No answer (yet).
No answer (yet).

FIGURE E.20: von Mises distribution

Answer to Exercise 5.32.

No answer (yet).

FIGURE E.21: inverse Gaussian distributions

Answer to Exercise 5.33.

$\int_c^\infty c/w^3\, dy = 1/(2c)$ and so $c = 1/2$.
$\operatorname{E}[W] = \int_{1/2}^\infty w/(2w^3) \, dy = 1$.
$\operatorname{E}[W^2] = \int_{1/2}^\infty w^2/w^3\, dy$ which does not converge; the variance is undefined.

Answer to Exercise 5.34.

$k > 0$
Differentiating: $f_X(x) = \alpha k^\alpha x^{-\alpha - 1}$.
$\operatorname{E}[X] = \alpha k/(\alpha - 1)$. Also, $\operatorname{E}[X^2] = \alpha k^2/(\alpha - 2)$, and so $\operatorname{var}[X] = \alpha k^2/[(\alpha - 2)(\alpha - 1)^2]$.
No answer (yet).
See below.
$\Pr(X > 4 \cap X < 5) = \Pr(4 < X < 5) = F(5) - F(4) = (3/4)^3 - (3/5)^3 = 0.205875$. Also, $\Pr(X < 5) = 1 - (3/5)^3 = 0.784$. So the prob. is $0.205875/0.784 = 0.2625957$.
No answer (yet).

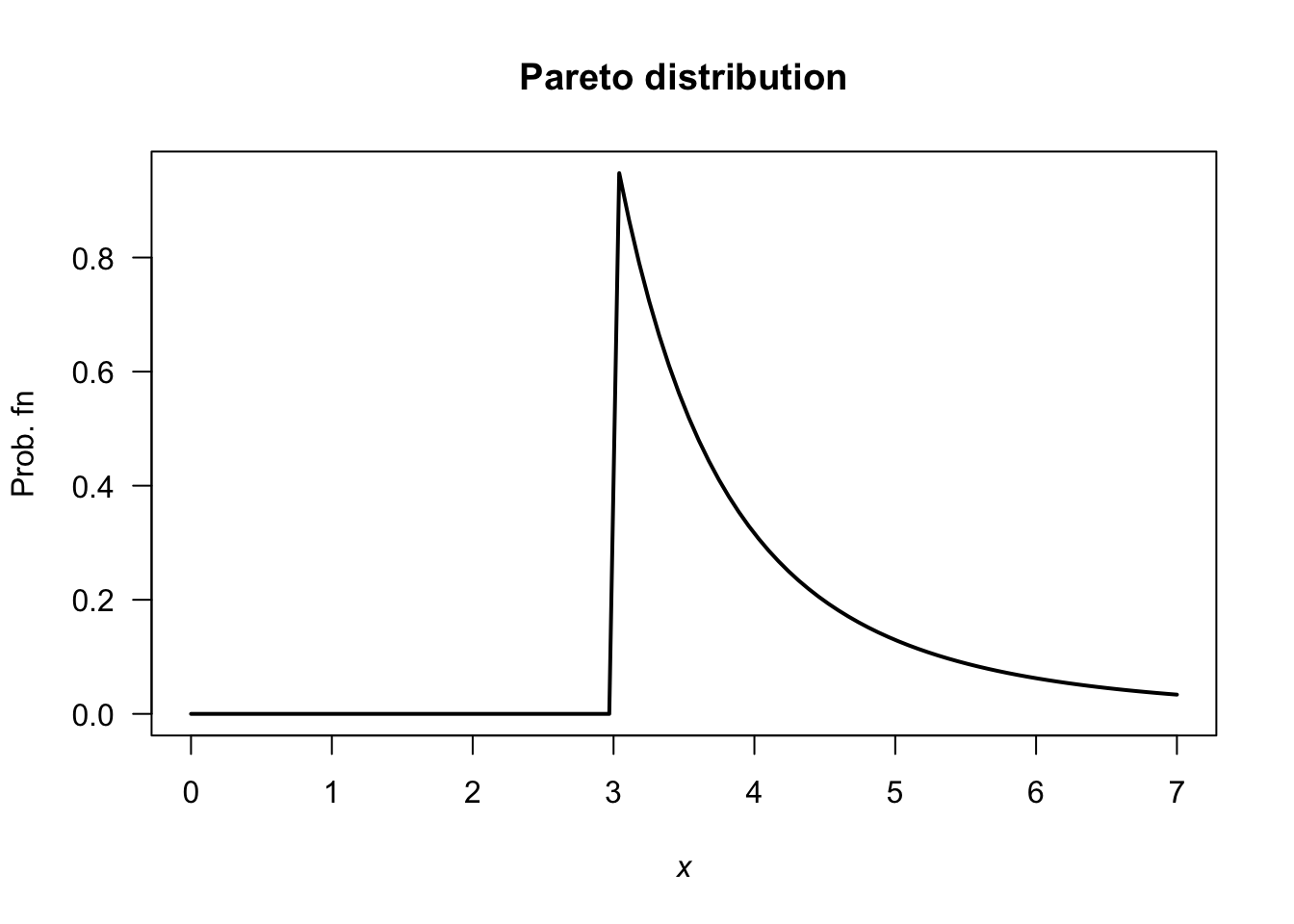
FIGURE C.1: A Pareto distribution

Answer to Exercise 5.36.

$\operatorname{E}(X) = \sum_{x = 1}^K x. p_X(x) = (1/6) + \sum_{x = 2}^K 1(x - 1)$. $\operatorname{E}(X^2) = \frac{1}{K} + \sum_{x=2}^K \frac{x}{x - 1}$ with no closed form, so the variance is a PITA. No closed form!
See Fig. E.22.
Applying the definition: \[ M_X(t) = \operatorname{E}(\exp(tX)) = \frac{1}{K} + \left( \frac{\exp(2t)}{2\times 1} + \frac{\exp(3t)}{3\times 2} + \frac{\exp(4t)}{4\times 3} + \dots + \frac{\exp(Kt)}{K\times (K - 1)}\right). \]

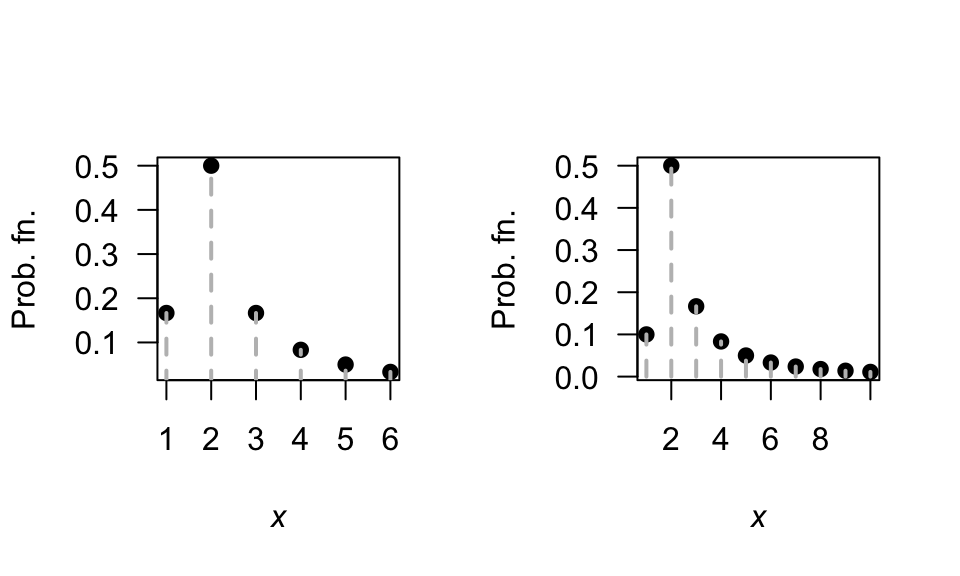
FIGURE E.22: The Soliton distribution

Answer to Exercise 5.40.

Since $M_X(t) = \lambda/(\lambda - t)$, then $M_X(it) = \lambda/(\lambda - it)$. Then \[\begin{align*} f_X(x) &= \int_{-\infty}^{\infty} M_X(it) ] \exp(-itx)\, dt \\ &= \int_{-\infty}^{\infty} \frac{\lambda}{\lambda - it} (\cos(-tx) + \sin(-tx))\, dt\\ &= \int_{-\infty}^{\infty} \frac{\lambda(\lambda + it)}{\lambda^2 + t^2} (\cos(tx) - \sin(tx))\, dt \\ &= \int_{-\infty}^\lambda \frac{\lambda}{\lambda^2 + t^2} (\lambda\cos(tx) + t\sin(tx))\, dt. \end{align*}\]

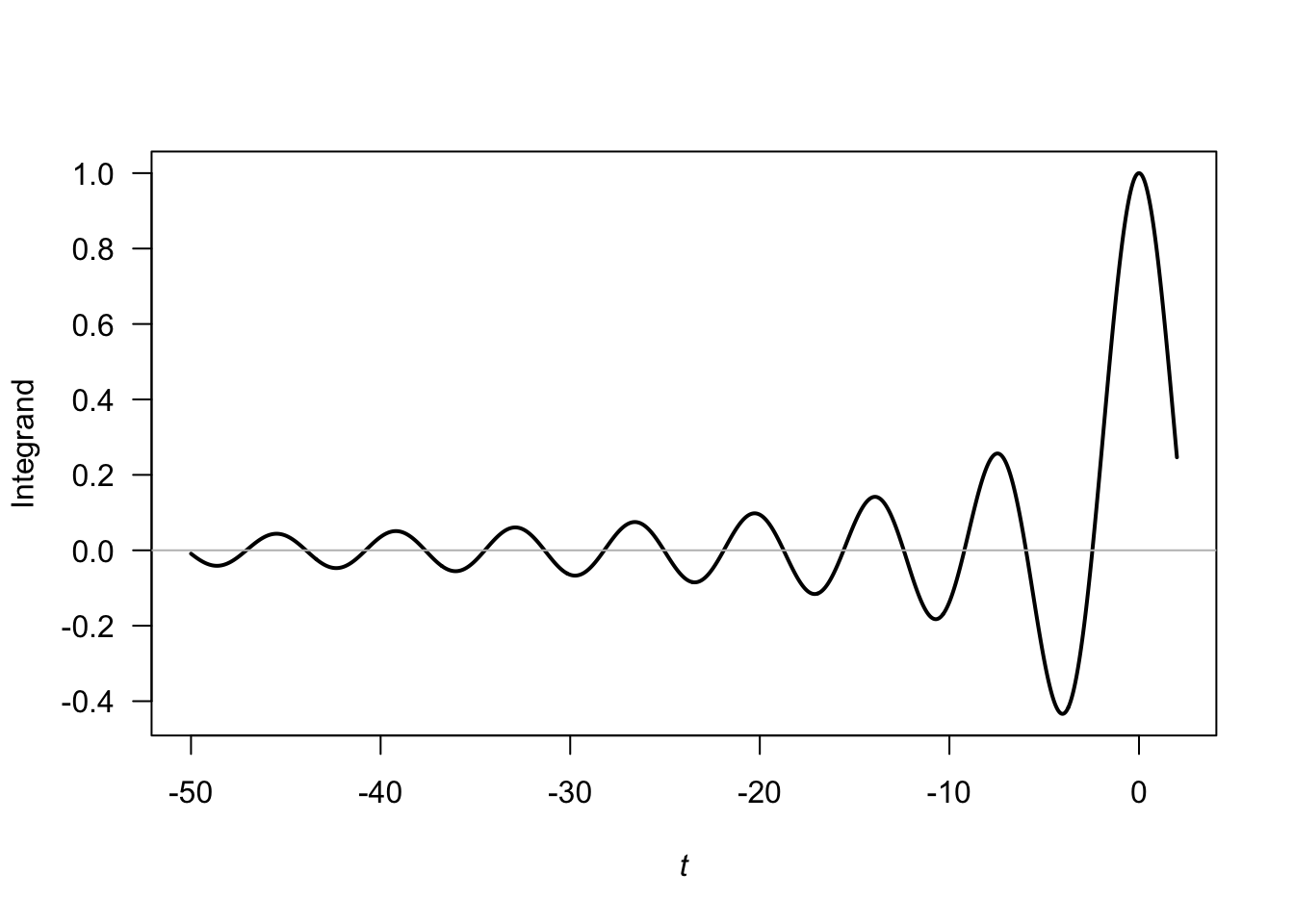
FIGURE E.23: The integrand

Answer to Exercise 5.44.

$\operatorname{E}[X] = (n + 1) - n (1 - p)^n$.
$\operatorname{E}[X^2] = (1 - p)^n + 25 - 25(1 - p)^n$, so $\operatorname{var}[X] = 16(1 - p)^n[ 1 - (1 - p)^n]$.
As $p \to 0$ (i.e., no-one has the disease), the expected number of tests is one (with no variation). As $p \to 1$ (i.e., everyone has the disease), the expected number of tests is five (with no variation).
Using $\operatorname{E}[X] > n$, solve to find $p > 1 - (1/n)^{1/n}$.
See Fig. E.24.
With $n = 4$, the expected number of tests saved is $4 - (5 - 4(1-p)^4) \approx 1.6244$. So doing this $50$ times (i.e., $50 \times 4 = 200$) would save $50\times 1.6244 \times 15 = 1218.3$; about $1220 in cost savings.

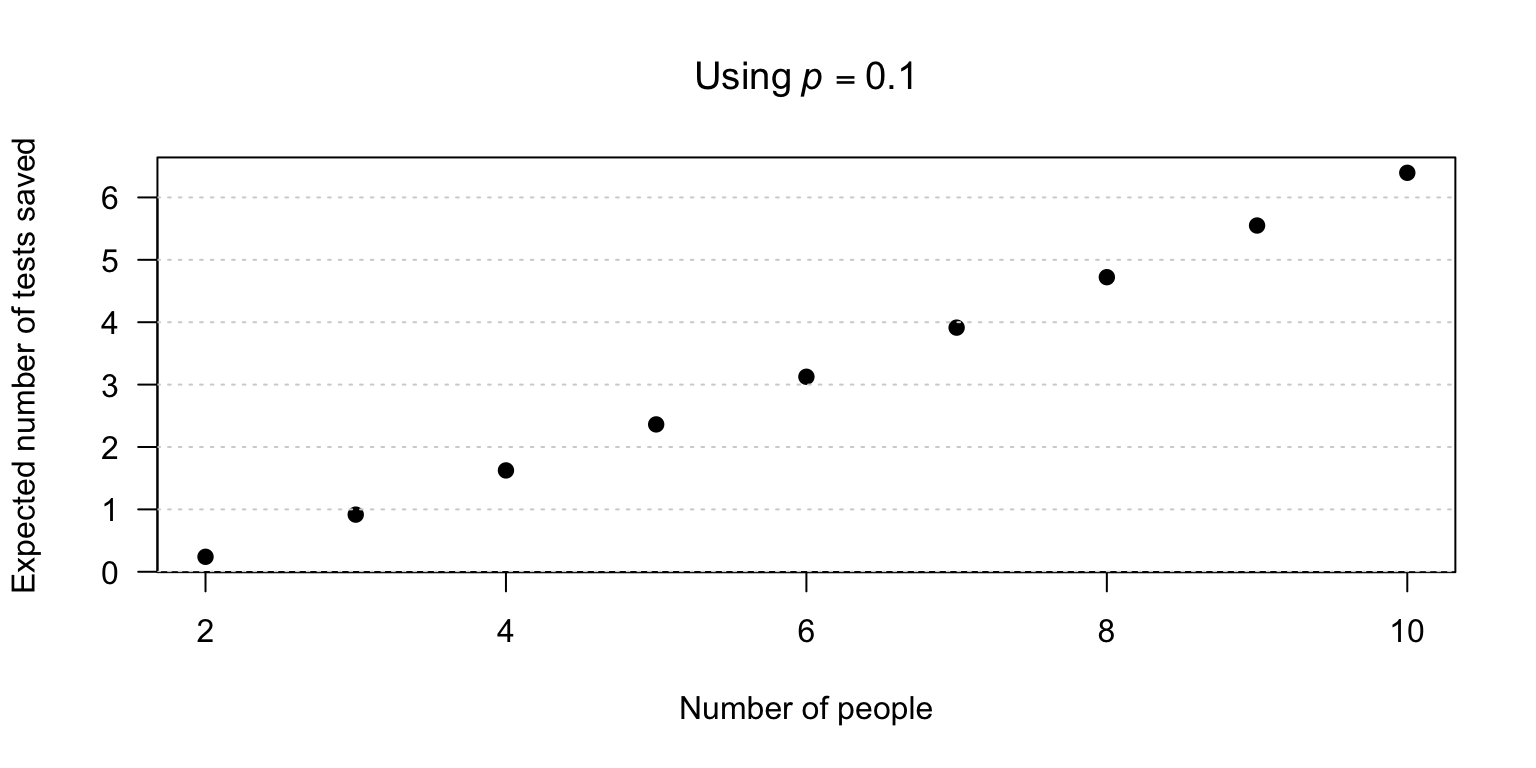
FIGURE E.24: The expected number of tests saved by pooling

$\Pr(\text{Need individual tests})$ ${}={}$ $\Pr(\text{Pooled test is positive})$ ${}={}$ $1 - \Pr(\text{Pooled test is negative})$ ${}={}$ $1 - \Pr(\text{All individuals are negative})$ ${}={}$ $1 -(0.9)^ 4 = 0.3439$. So the PMF of $N$, the number of tests needed, is \[ p_N(n) = \begin{cases} 0.6561 & \text{for $n = 1$ (i.e., pooled test only)};\\ 0.3439 & \text{for $n = 5$ (i.e., one pooled test, olus four individual tests)} \end{cases} \] Then $\operatorname{E}(X) = (0.6561 \times 1) + (0.3439 \times 5) = 2.3756$ and $\operatorname{E}(X^2) = (0.6561 \times 1^2) + (0.3439 \times 5^2) = 9.2536$ so that $\operatorname{var}(X) = 3.610125$. So for a pool of four people, rather than four tests we would expected to have to conduct $2.3756$ tests, a saving of $4 - 2.3756 = 1.6244$ tests.

If $200$ people in total, testing each individual would cost $200\times 15 = \$3000$. With $n = 4$, a total of $50$ pools are created, and each pool saves $1.6244$ tests, so the total number of tests expected to be saved in $50 \times 1.6244 = 81.22$; at $15 each, the saving is $\$1218.30$.

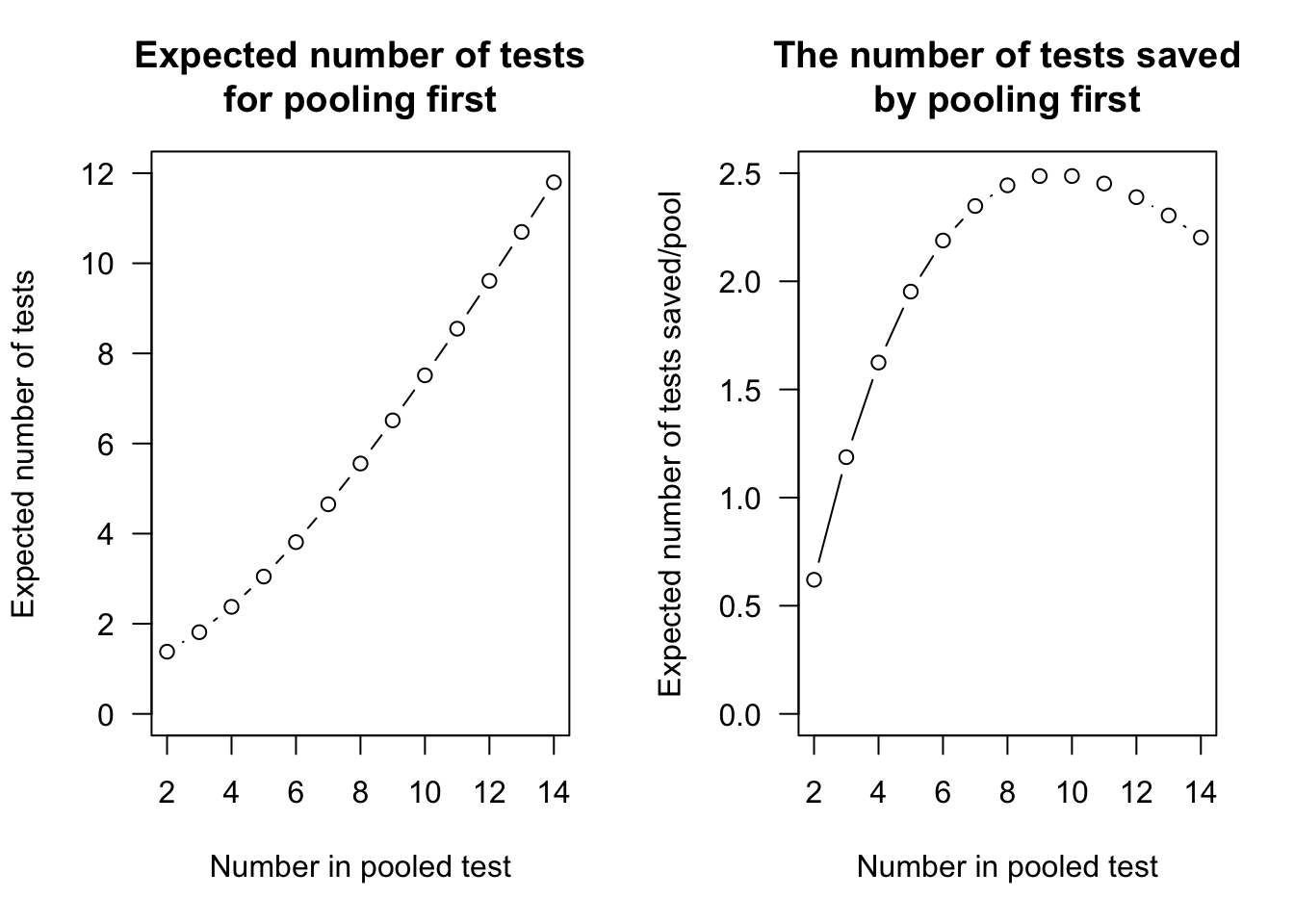
FIGURE E.25: The advantage of initial pooled testing

Answer to Exercise 5.46.

$\operatorname{E}[X] = 7/2$.
$\operatorname{MAD}[X] = 1.5$.

Answer to Exercise 5.49.

Plot not shown, but a quadratic symmetric about $x = 0$.
All odd moments are zero since distribution symmetric: $\operatorname{E}[X] = 0$. $\operatorname{var}[X] = \operatorname{E}[X^2] = 3/5$.
Odd moment, and distribution obviously symmetric; skewness is zero.
$\operatorname{E}[X^4] = 3/7$, so kurtosis is $\mu_4/\mu^2_2 = (3/7)/(3/5)^2 = 25/21$. Hence, the excess kurtosis is $25/21 - 3 = -38/21$.
No values in the extreme values like a normal; all values are contained within $-1 < x < 1$.

Answer to Exercise 5.50.

Plot not shown, but straight line from $(0, 0)$ to $(2, 1)$.
$\operatorname{E}[X^r] = 2^{r + 1}/(r + 2)$.
$\operatorname{E}[X] = 4/3$; $\operatorname{var}[X] = 2 - (4/3)^2 = 14/9$.
$\operatorname{E}[ (X - \mu)^3] = -8/135$, so skewness is $\mu_3 / \mu_2^{3/2} = (-8/135)/(14/9)^{3/2} = -2\sqrt{14}/245$. Negative value: left skewed; bulk of probability to the right side.
$\operatorname{E}[(X - \mu)^4] = 16/135$, so kurtosis is $\mu_4/\mu^2_2 = (16/135)/(14/9)^2 = 12/245$. Hence, the excess kurtosis is $12/245 - 3 = -723/245$ No values in the extreme values like a normal; all values are contained within $0 < x < 2$.

E.6 Answers for Chap. 6

Answer to Exercise 6.1.

For $0 < x < 2$, the transformation is one-to-one. The inverse transform is $X = Y^{1/3}$, and so $0 < y < 8$.

$F_Y(y) = \Pr(Y\le y) = \Pr(X^3 \le y) = \Pr(X\le y^{1/3}) = F_X( y^{1/3}) = \int_{u = 0}^{y^{1/3}} u/2\,du = u^2/4\Big|_{u = 0}^{u = y^{1/3}} = y^{2/3}/4.$ Differentiate to find the PDF: $\frac{d}{dy} y^{2/3}/4 = y^{-1/3}/6$. The PDF of $Y$ is \[ f_Y(y) = \begin{cases} y^{-1/3}/6 & \text{for $0 < y < 8$};\\ 0 & \text{otherwise}. \end{cases} \]
Since $w(y) = y^{1/3}$, then $w'(y) = y^{-2/3}$. Then: \[\begin{align*} f_Y(y) &= f_X(y) |J|\\ &= y^{1/3}/2 \times \overbrace{y^{-2/3}/3}^{|J|} \\ &= y^{-1/3}/6. \end{align*}\] So the PDF of $Y$ is as above.

Answer to Exercise 6.2.

First:

For $X_1 = 0$, $X_2= 0$ (with prob: $0$): $Y_1 = 0$; $Y_2 = 0$;
For $X_1 = 0$, $X_2= 1$ (with prob. $1/6$): $Y_1 = 1$; $Y_2 = 1$;
For $X_1 = 1$, $X_2= 0$ (with prob. $2/6$): $Y_1 = 1$; $Y_2 = 0$;
For $X_1 = 1$, $X_2= 1$ (with prob. $3/6$): $Y_1 = 2$; $Y_2 = 1$.

Effectively, the first line can be ignored (since the probability is zero), so $Y_1 \in \{1, 2\}$ and $Y_2\in\{0, 1\}$.

From the above, the joint pf is shown in Table E.3.
Hence, from the table: \[ f_{Y_1}(y_1) = \begin{cases} 1/2 & \text{if $y_1 = 1$};\\ 1/2 & \text{if $y_1 = 2$};\\ 0 & \text{otherwise}. \end{cases} \]

TABLE E.3: The joint distribution of $Y_1$ and $Y_2$
	$Y_1 = 1$	$Y_1 = 2$
$Y_2 = 0$	$2/6$	$0$
$Y_2 = 1$	$1/6$	$3/6$

Answer to Exercise 6.3.

$Y \sim\text{Gam}(\sum\alpha, \beta)$.

Answer to Exercise 6.4.

Transformation is not 1-1; and $Y > 0$. Then: \[\begin{align*} F_Y(y) &= \Pr(Y < y)\\ &= \Pr( X^1 < y)\\ &= \Pr( -\sqrt{y} < X < \sqrt{y} ) \quad\text{(draw a diagram!)}\\ &= \int_{-\sqrt{y}}^{\sqrt{y}} \frac{1}{\pi(1 + x^2)}\, dx\\ &= \frac{2}{\pi} \tan^{-1}(\sqrt{y}). \end{align*}\] and so \[\begin{align*} f_Y(y) &= \frac{d}{dy} \frac{2}{\pi} \tan^{-1}(\sqrt{y})\\ &= \frac{1}{\pi(y + 1)\sqrt{y}}\quad\text{for $y > 0$}. \end{align*}\]

Answer to Exercise 6.5.

Differentiating: \[ f_X(x) = \begin{cases} 1 & \text{for $-1/2 < x < /1/2$};\\ 0 & \text{elsewhere}. \end{cases} \]
First: this transformation is not 1:1 (Fig. E.26). See that $X = \pm\sqrt{4 - Y}$, and that $3.75 < Y < 4$. So, \[\begin{align*} F_Y(y) &= \Pr(Y < y) \\ &= 1 - \Pr( -\sqrt{4 - y} < X < \sqrt{4 - y} )\\ &= 1 - \int_{-\sqrt{4 - y}}^{\sqrt{4 - y}} 1\, dx\\ &= 1 - 2\sqrt{4 - y}, \end{align*}\] and so, differentiating: \[ f_Y(y) = \frac{1}{\sqrt{4 - y}} \quad\text{for $3.75 < Y < 4$} \]

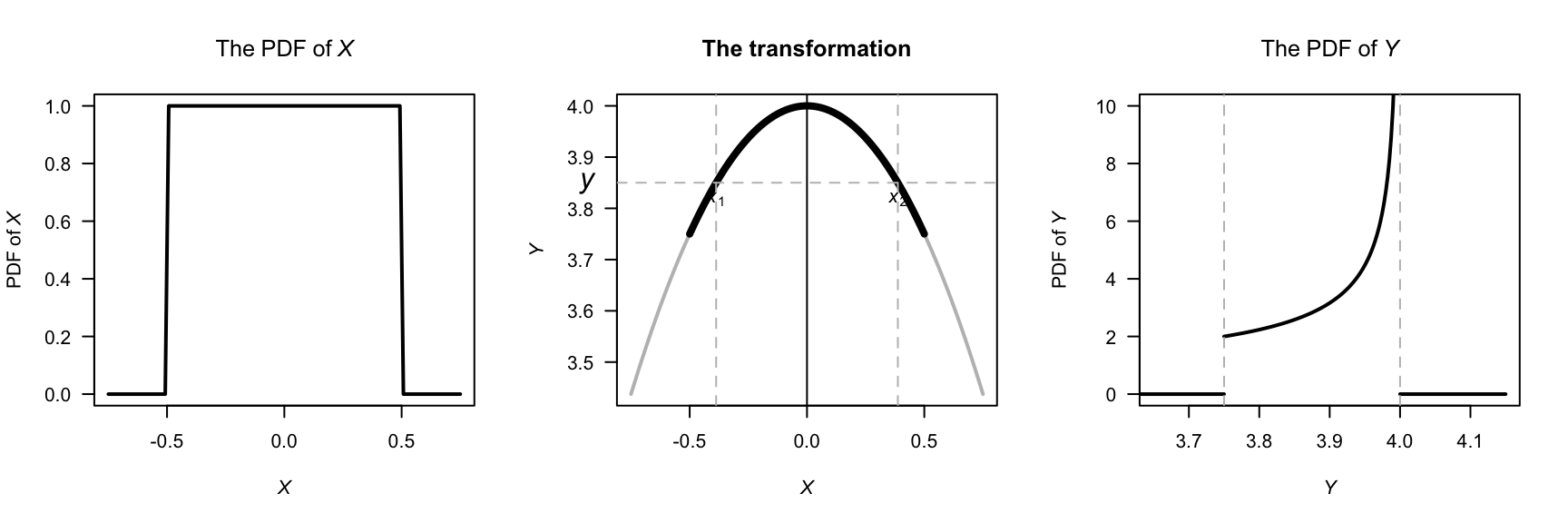
FIGURE E.26: The transformation

Answer to Exercise 6.6.

Given that $f(\theta) = 4/\pi$ for $0 < \theta< \pi/4$, and hence $0 < D < (v^2/g)$. Then: \[\begin{align*} F_D(d) = \Pr(D < d) &= \Pr( v^2/g\sin2\theta < d) \\ &= \Pr(\theta < \frac{1}{2} \sin^{-1}(d g/v^2 ) \\ &= \int_0^{\sin^{-1}(d g/v^2 )/2} \frac{4}{\pi}\, d\theta \\ &= \frac{2}{\pi} \sin^{-1} \left( \frac{dg}{v^2} \right). \end{align*}\] So \[ f_D(d) = \frac{2g}{\pi}\frac{1}{\sqrt{v^4 - d^2 g^2}}\quad\text{for $0 < D < v^2 /g$}. \]

Alternatively: see that $D = v^2\sin 2\theta/g \Rightarrow sin 2\theta = Dg/v^2$, and so \[ \frac{dd}{d\theta} = \frac{2v^2}{g}\cos 2\theta. \] Then, \[\begin{align*} f_D(d) &= \frac{4}{\pi} \left| \frac{g}{2 v^2\cos 2\theta} \right|\\ &= \frac{2g}{\pi v^2 \cos2\theta}\\ &= \frac{2g}{\pi \sqrt{v^4 - d^2 g^2}} \end{align*}\] after (e.g.) drawing the right-angled triangle to re-write $\sin 2\theta = Dg/v^2$. See Fig. E.27.

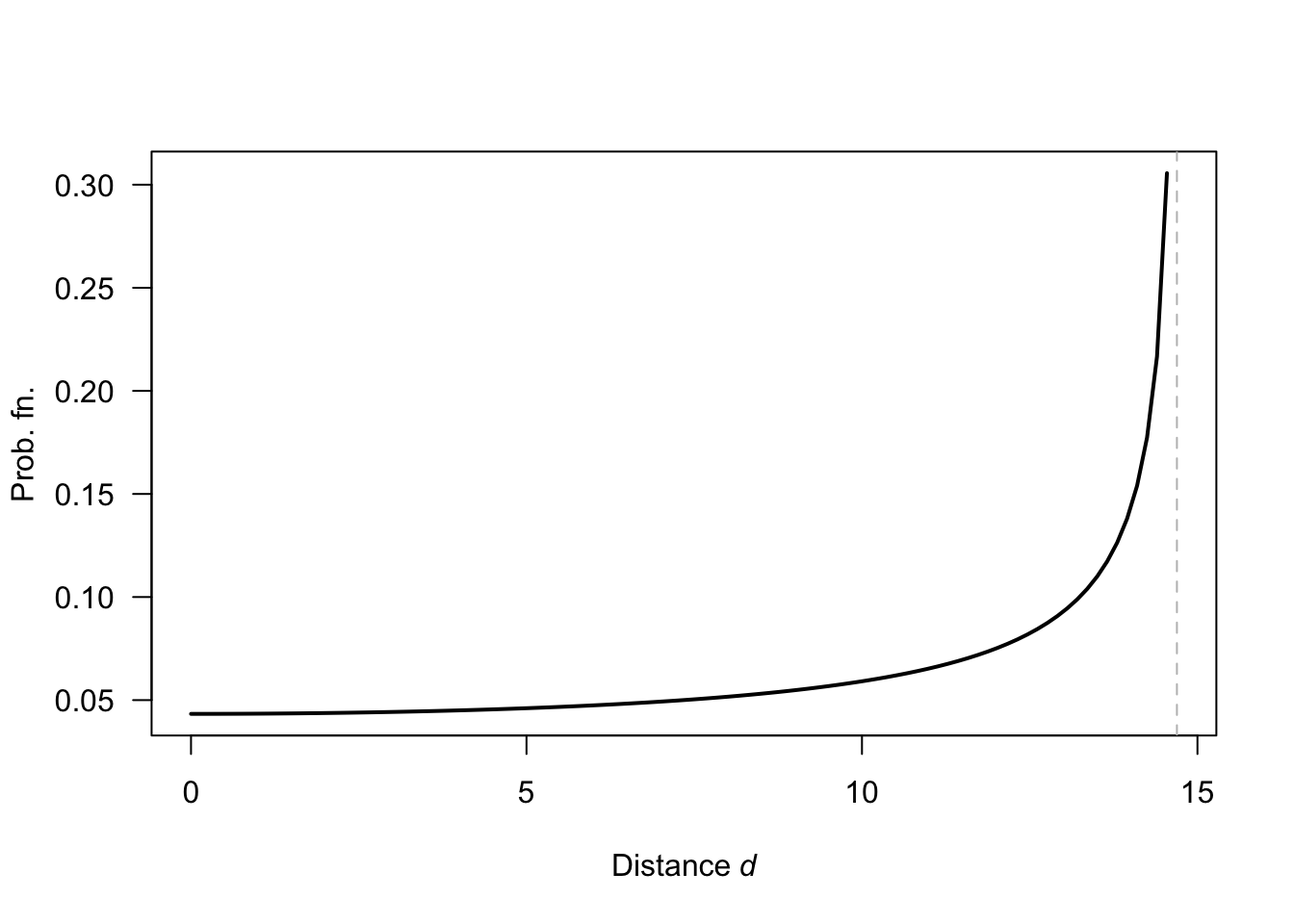
FIGURE E.27: The distance travelled by a projectile

Answer to Exercise 6.7. Proceed: \[\begin{align*} F_Y(y) &= \Pr(Y \le y)\\ &= \Pr(X \ge \exp(-y/\alpha)) \qquad\text{note the change of direction!}\\ &= \int_{\exp(-y/\alpha)}^1 1\, dx \end{align*}\] so that $f_Y(y) = \frac{1}{\alpha} \exp(-y/\alpha)$ for $y > 0$, which is the exponential distribution.

Answer to Exercise 6.8.

$\operatorname{E}[W] = -1/3$; $\operatorname{var}[W] = 17/9\approx 1.8889\dots$.
$\Pr(V = 0) = 1/2$; $\Pr(V = 4) = 1/2$.
Find: \[ F_W(w) = \begin{cases} 0 & \text{for $w < -2$};\\ 1/3 & \text{for $-2 \le w < 0$};\\ 5/6 & \text{for $0 \le w < 2$};\\ 1 & \text{for $w \ge 2$}. \end{cases} \]

Answer to Exercise 6.10.

First see that $Y = \log X$. Then: \[\begin{align*} F_Y(y) &= \Pr(Y < y) \\ &= \Pr( \exp X < y)\\ &= \Pr( X < \log y)\\ &= \Phi\big((\log y - \mu)/\sigma\big) \end{align*}\] by the definition of $\Phi(\cdot)$.
Proceed: \[\begin{align*} f_Y(y) &= \frac{d}{dy} \Phi\big((\log y - \mu)/\sigma\big) \\ &= \frac{1}{y} \Phi\big((\log y - \mu)/\sigma\big) \\ &= \frac{1}{y\sqrt{2\pi\sigma^2}} \exp\left[\left( -\frac{ (\log y - \mu)^2}{\sigma}\right)^2\right] \end{align*}\] since the derivative of $\Phi(\cdot)$ (the df of a standard normal distribution) is $\phi(\cdot)$ (the PDF of a standard normal distribution).
See Fig. E.28.
See below: About $0.883$.

par( mfrow = c(2, 2))

x <- seq(0, 8,
         length = 500)

plot( dlnorm(x, meanlog = log(1), sdlog = 1) ~ x,
      xlab = expression(italic(y)),
      ylab = "PDF",
      type = "l",
      main = expression(Log~normal*":"~mu==1~and~sigma==1),
      lwd = 2,
      las = 1)
plot( dlnorm(x, meanlog = log(3), sdlog = 1) ~ x,
      xlab = expression(italic(y)),
      ylab = "PDF",
      type = "l",
      main = expression(Log~normal*":"~mu==3~and~sigma==1),
      lwd = 2,
      las = 1)
plot( dlnorm(x, meanlog = log(1), sdlog = 2) ~ x,
      xlab = expression(italic(y)),
      ylab = "PDF",
      main = expression(Log~normal*":"~mu==1~and~sigma==2),
      type = "l",
      lwd = 2,
      las = 1)
plot( dlnorm(x, meanlog = log(3), sdlog = 2) ~ x,
      xlab = expression(italic(y)),
      ylab = "PDF",
      main = expression(Log~normal*":"~mu==3~and~sigma==2),
      type = "l",
      lwd = 2,
      las = 1)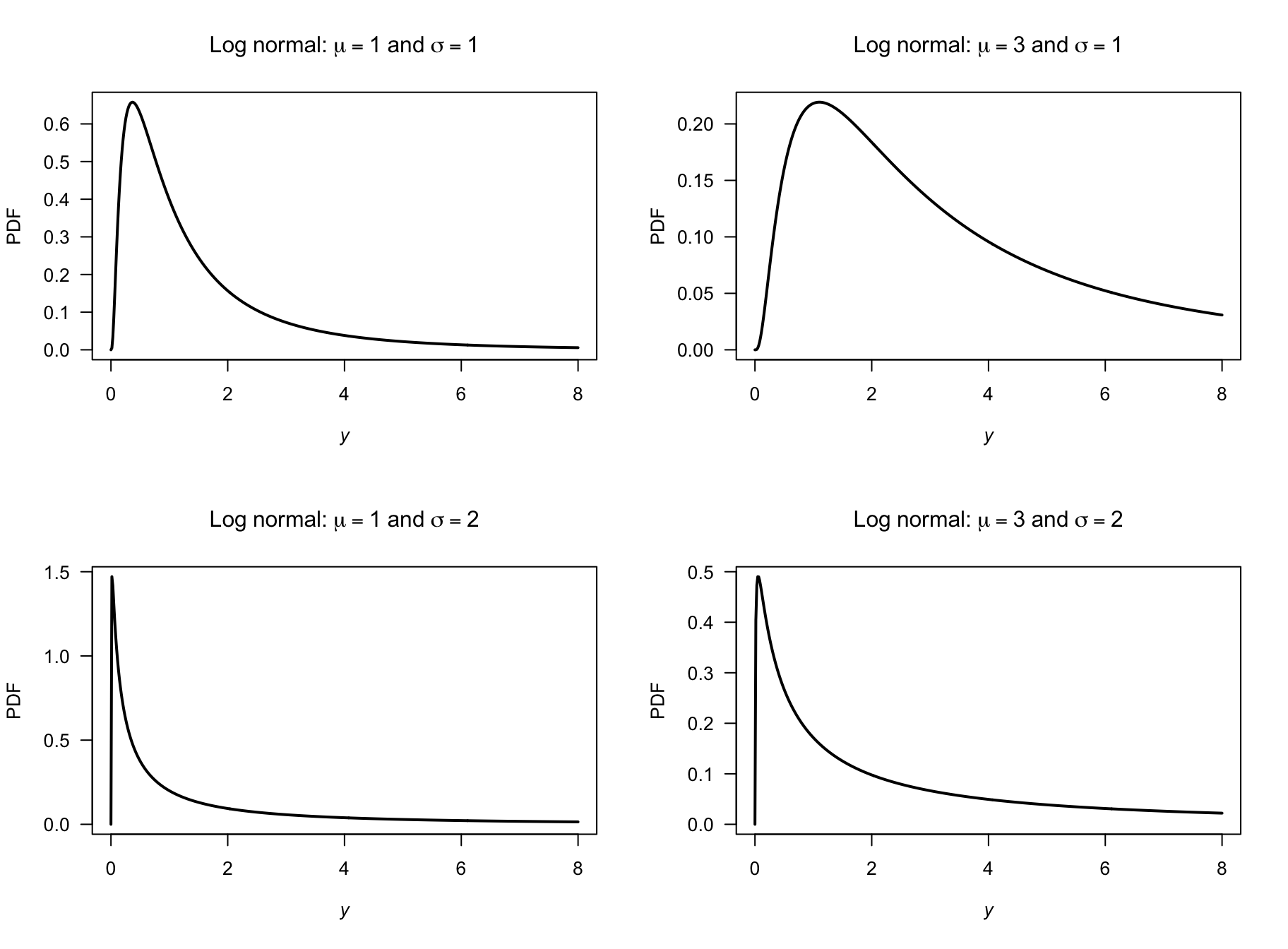

FIGURE E.28: Log-normal distributions

(1 - plnorm(2, meanlog=2, sdlog=2)) / 
  (1 - plnorm(1, meanlog=2, sdlog=2))
#> [1] 0.8834182

Answer to Exercise 6.11. See that $Y\in\{0, 1, \sqrt{2}, \sqrt{3}, 2\}$ and so \[ \Pr(Y = y) = \binom{4}{y^2} (0.2)^{y^2} (0.8)^{4 - y^2} \quad \text{for $y = 0, 1, \sqrt{2}, \sqrt{3}, 2$}. \]

Answer to Exercise 6.12.

First, see the relationships: \[\begin{align*} X = 1 &\to Y = (X - 3)^2 = 4;\\ X = 2 &\to Y = (X - 3)^2 = 1;\\ X = 3 &\to Y = (X - 3)^2 = 0;\\ X = 4 &\to Y = (X - 3)^2 = 1. \end{align*}\] So adding probabilities as appropriate: \[ p_Y(y) = \begin{cases} 9/30 & \text{for $y = 0$}\\ 20/30 & \text{for $y = 1$}\\ 1/30 & \text{for $y = 4$}\\ 0 & \text{elsewhere}. \end{cases} \]

Answer to Exercise 6.16.

For the given beta distribution, $\operatorname{E}(V) = 0.287/(0.287 + 0.926) = 0.2366...$ and $\operatorname{var}(V) = 0.08161874$.

$\operatorname{E}(S) = \operatorname{E}(4.5 + 11V) = 4.5 + 11\operatorname{E}(V) = 7.10$ minutes. $\operatorname{var}(S) = 11^2\times\operatorname{var}(V) = 9.875$ minutes².
$V\in (4.5, 15.5)$. See Fig. E.29.
This corresponds to $V = 10.5/11 = 0.9545455$, so $\Pr(S > 15) = \Pr(V > 0.9545455) = 0.01745087$.
With $V$, the largest 20% correspond to $V = 0.004080076$, so that $S = 4.544881$; the quickest $20%$ are within $4.54$ minutes.

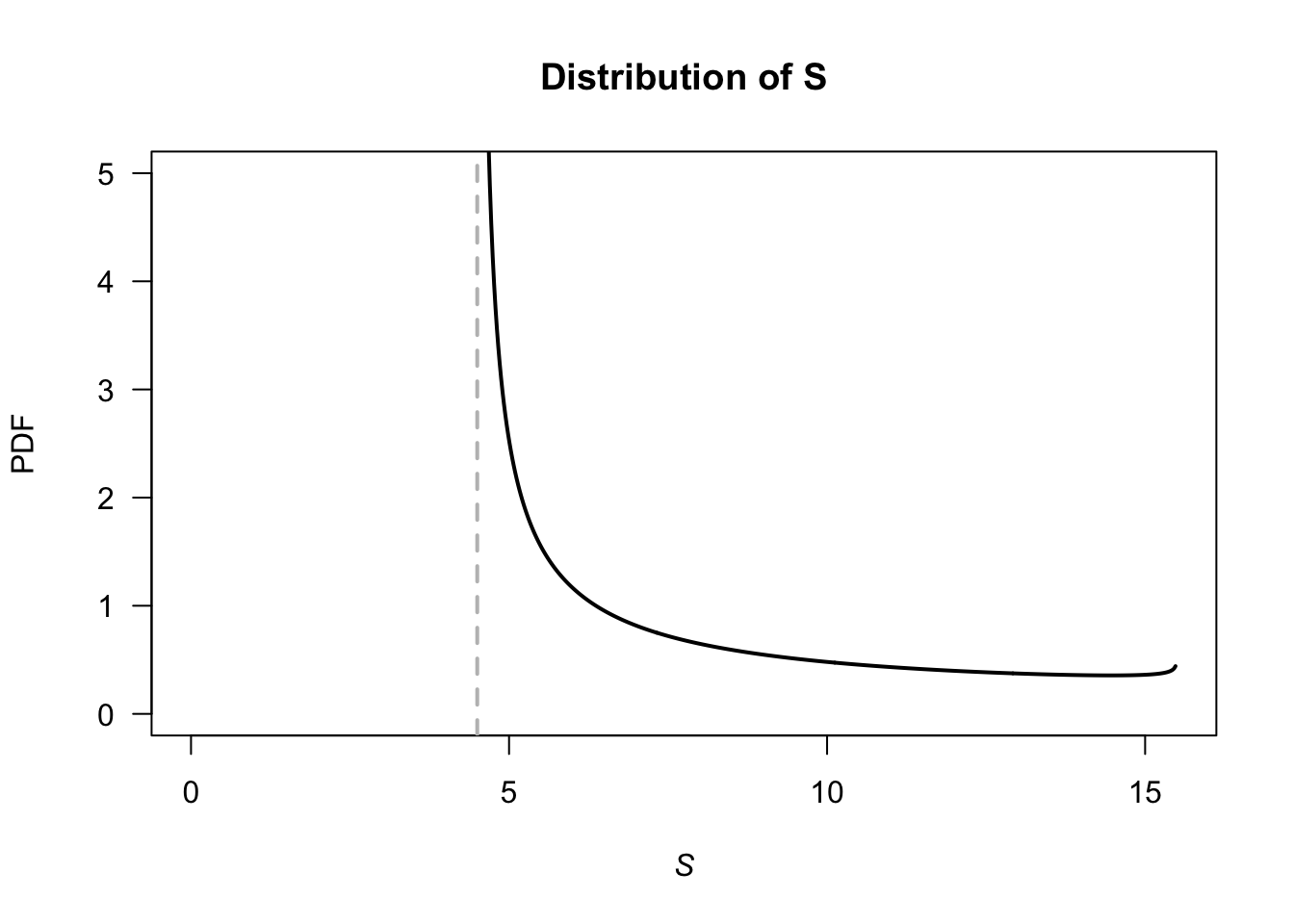
FIGURE E.29: Service times

#> [1] 0.01745087
#> [1] 4.50408

Answer to Exercise 6.18.

Care is needed with the interval: it is not 1:1.

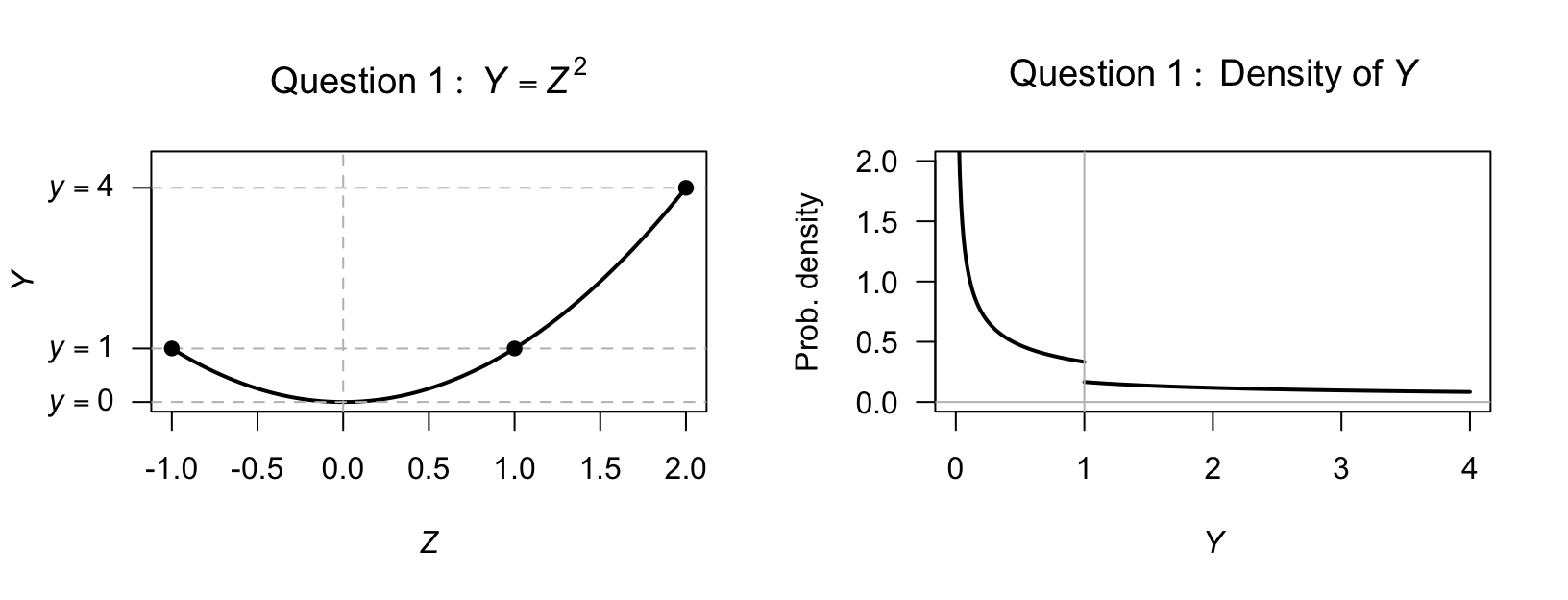
FIGURE E.30: Question 1

Note that $Y$ is defined over $0 < Y < 4$, and the transformation is not a 1:1 transformation (Fig. 1, left panel) over these values. To use the distribution function method, see that $0 < y < 1$ corresponds to $-\sqrt{Y} < z < \sqrt{Y}$, but $1 \le y \le 4$ corresponds to $-1 < z <\sqrt{Y}$. For $y < 1$: \[ F_Y(y) = \Pr(Y \le y) = \Pr(-\sqrt{y} < z < \sqrt{y}\,) = \int_{-\sqrt{y}}^{\sqrt{y}} \frac{1}{3}\, dz = \frac{2\sqrt{y}}{3}\quad \text{for $0 < y < 1$}. \] For $1 < y < 4$, start by writing $F_Y(y) = \Pr(Y \le y)$, but then take care to include $\Pr(Y < 1)$! \[ F_Y(y) = \Pr(Y \le 1) + \Pr(1 < Y < y) = \frac{2}{3} + \Pr(1 < z < \sqrt{y}\,) = \frac{2}{3} + \int_{1}^{\sqrt{y}} \frac{1}{3}\, dz = \frac{1 + \sqrt{y}}{3}. \] Hence (noting carefully where $y = 1$ in the PDF): \[ F_Y(y) = \begin{cases} 0 & \text{for $y \le 0$};\\ \frac{2\sqrt{y}}{3} & \text{for $0 \le y < 1$};\\ \frac{1 + \sqrt{y}}{3} & \text{for $1 \le y < 4$};\\ 1 & \text{for $y \ge 4$} \end{cases} \quad\text{so differentiating:}\quad f_Y(y) = \begin{cases} \frac{1}{3\sqrt{y}} & \text{for $0 < y < 1$};\\ \frac{1}{6\sqrt{y}} & \text{for $1 \le y < 4$};\\ 0 & \text{elsewhere}. \end{cases} \]
For all values of $Y$, the PDF is non-negative. In addition, $\int_Y f_Y(y)\, dy = 1$.
See Fig. E.30 (right panel).

Answer to Exercise 6.20. We have \[ f_X(x) = \begin{cases} 2x/3 & \text{for $0 \le x \le 1$}\\ (3 - x)/3 & \text{for $1 < x \le 3$} \end{cases} \] and hence \[ F_X(x) = \begin{cases} 0 & \text{for $x < 0$}\\ x^2/3 & \text{for $0 \le x \le 1$}\\ (6x - x^2 - 3)/6 & \text{for $1 < x \le 3$}\\ 1 & \text{for $x > 3$.} \end{cases} \] Since $Y = 6 - 2x$, $\mathcal{R}_X = (0, 3)$ maps to $\mathcal{R}_Y = (0, 6)$; more specifically, $0 \le x \le 1$ maps to $4 \le y \le 6$ and $1 < x \le 3$ maps to $0 < y \le 4$. Then: \[\begin{align*} F_Y(y) &= \Pr(Y \le y)\\ &= \Pr\left( x \ge \frac{6 - y}{2}\right)\\ &= 1 - \Pr\left( x \le \frac{6 - y}{2}\right)\\ &= 1 - F_X\left( x \le \frac{6 - y}{2}\right). \end{align*}\] So, when $0 \le x \le 1$ (i.e., $4\le y \le 6$): \[ F_Y(y) = \frac{12y - y^2 - 24}{12} \] and when $1 < x \le 3$ (i.e., $0 < y \le 4$): \[ F_Y(y) = \frac{y^2}{24} \] so that (CHECK LESS THAN, LESS THAN OR EQUAL signs!!!!!!!!!!!) \[ f_Y(y) = \begin{cases} y/12 & \text{for $0 < y \le 4$}\\ (6 - y)/6 & \text{for $4 \le y \le 6$.} \end{cases} \]

Answer to Exercise 6.21. Not a 1:1 function so care is needed. $f_X(x) and $F_X(x)$ are given above. Since $Z = (X - 2)^2$, $\mathcal{R}_X = (0, 3)$ maps to $\mathcal{R}_Z = (0, 4)$; more specifically, $0 \le x \le 1$ maps to $1 \le z \le 4$ and $1 < x \le 3$ maps to $0 < z \le 1$. First consider the case $0\le z\le 1$: \[\begin{align*} F_Z(z) &= \Pr(Z \le y)\\ &= \Pr(2 - \sqrt{Z} \le X \le 2 + \sqrt{Z})\\ &= F_X(2 + \sqrt{z}) - F_X(2 - \sqrt{z})\\ &= 2\sqrt{z} / 3. \end{align*}\] Then, when $1\le z \le 4$: \[\begin{align*} F_Z(z) &= \Pr(Z \le z)\\ &= F_Z(1) + \Pr(2 - \sqrt{Z} \le X\le 1)\\ &= \frac{2}{3} + \frac{4\sqrt{z} - z - 3}{3}\\ &= \frac{4\sqrt{z} - z - 1}{3}. \end{align*}\] So we write \[ F_Z(z) = \begin{cases} 0 & \text{for $z < 0$}\\ 2\sqrt{z}/3 & \text{for $0 < z < 1$}\\ (4\sqrt{z} - z - 1)/3 & \text{for $1 < z < 4$}\\ 1 & \text{for $z > 4$.} \end{cases} \] Note that $F_Z(4) = 1$ and $F_Z(0) = 0$ as required. Furthermore, the two parts both give $F_Z(1) = 2/3$. Then, so that (CHECK LESS THAN, LESS THAN OR EQUAL signs!!!!!!!!!!!) \[ f_Z(z) = \begin{cases} 1/(3\sqrt{z}\,) & \text{for $0 < z \le 1$}\\ \left(2/\sqrt{z} - 1\right)/3 & \text{for $1 \le z \le 4$}\\ 0 & \text{elsewhere.} \end{cases} \]

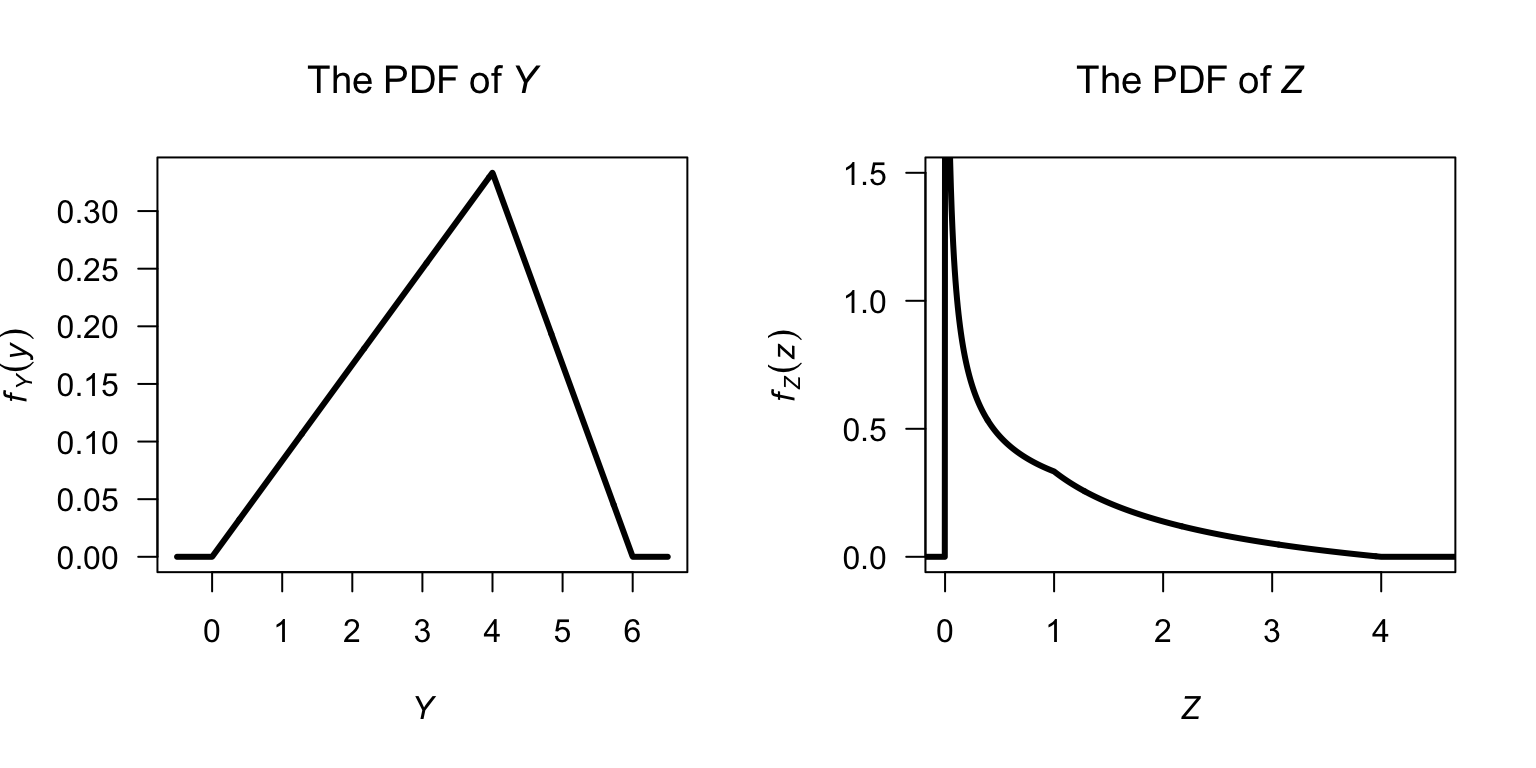
$The pdf of the transformed rvs\ $Y$ and\ $Z$.$

FIGURE E.31: The pdf of the transformed rvs $Y$ and $Z$.

Answer to Exercise 6.22. $f_V(v) = f_T(D/v)\left| \frac{dT}{dV}\right| = f_T(D/v) \frac{D}{v^2}$; and so \[ f_V(v) = \begin{cases} \displaystyle\frac{D(va + v\mu - D)}{a^2\,v^3} & \text{for $D/(\mu + \Delta) < v < D/\mu$}\\[6pt] \displaystyle\frac{D(va - v\mu + D)}{a^2\,v^3} & \text{for $D/\mu < v < D/(\mu - a)$} \end{cases} \] as shown in Fig. E.32 (left panel).

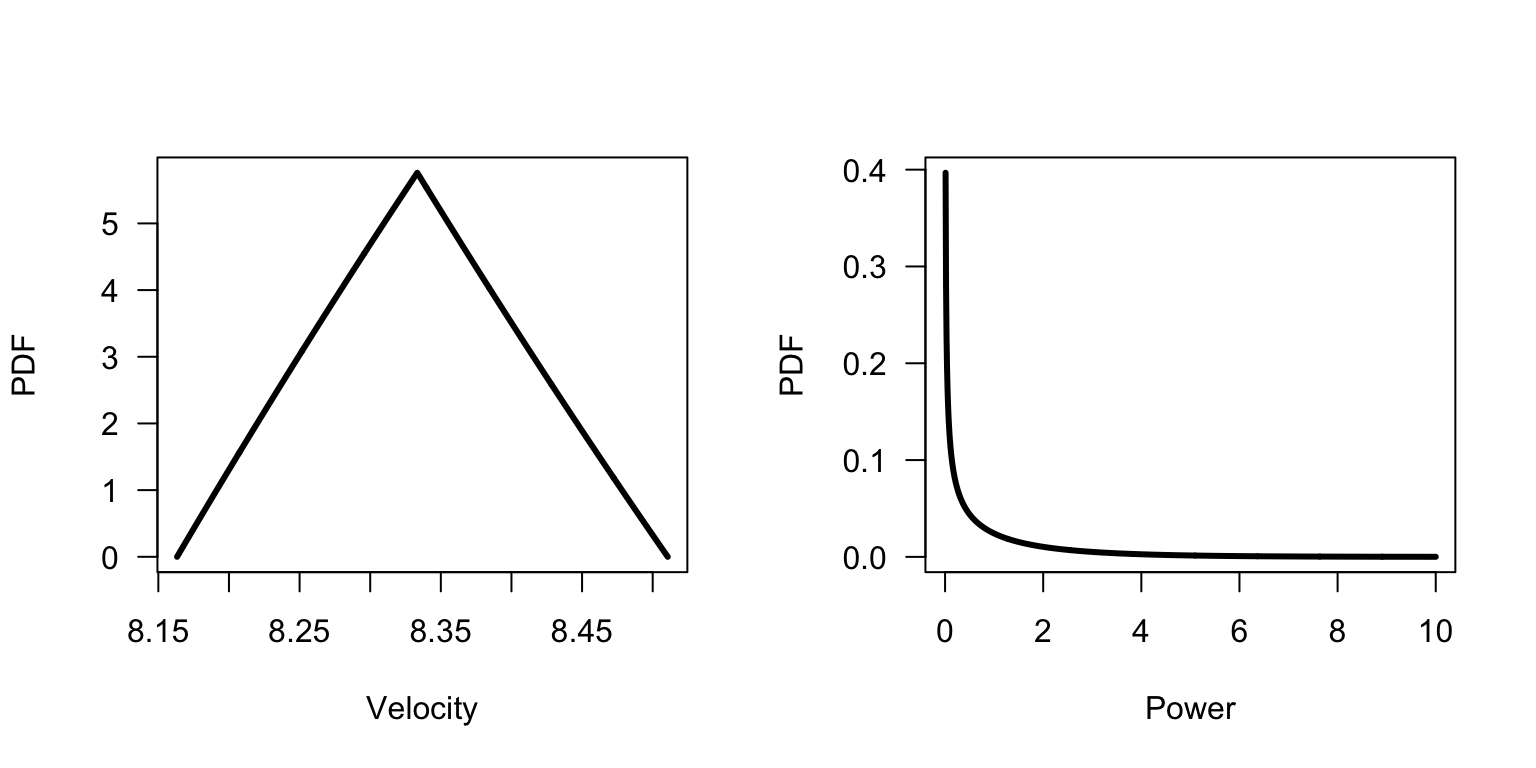
$The probability density function for the random variable\ $V$, the run velocity.$

FIGURE E.32: The probability density function for the random variable $V$, the run velocity.

Answer to Exercise 6.23. $f_P(p) = f_V(\sqrt{pR}) \frac{1}{2} \sqrt{\frac{R}{p}}$ and so \[ f_P(p) = \frac{\sqrt{R}}{\sqrt{2p\pi\sigma^2}} \exp\left\{-\frac{pR}{2\sigma^2}\right\} \] as shown in Fig. E.32 (right panel).

E.7 Answers for Chap. 7

Answer to Exercise 7.1. From what is given: $p_X(x; n, 1 - p) = \binom{n}{x} (1 - p)^x p^{n - x}$. Then, define $Y = n - X$ and hence $f_Y(y) = \binom{n}{y} p^y (1 - p)^{n - y}$, which is $f_Y(y) = \binom{n}{n - x} p^{n - x} (1 - p)^{n}$. It is easy to show $\binom{n}{x} = \binom{n}{n - x}$ and hence $f_X(x)$ and $f_Y(y)$ are equivalent.

Answer to Exercise 7.2.

Care: The geometric is parameterised so that $x$ is the number of failures before a success (not the number of trails). Similarly for the negative binomial.

sum( dbinom(10:25, # Part 1
            size = 25,
            prob = 0.30) )
#> [1] 0.189436
sum( dbinom(0:9,  # Part 2
            size = 25,
            prob = 0.30) )
#> [1] 0.810564
sum( dbinom(5:10,  # Part 3
            size = 25,
            prob = 0.30) )
#> [1] 0.8117281
dgeom(x  = 5,  # Part 4: 5 fails before 1st success
      prob = 0.30)
#> [1] 0.050421

sum( dgeom(x  = 7:50,  # Part 5: Num. fails! 
           prob = 0.30) )
#> [1] 0.08235429

# Part 6; This means 5 fails, before 3rd success
dnbinom(x = 5,
        prob = 0.30,
        size = 3)
#> [1] 0.09529569

Assumes independence of people, and a constant probability.

Answer to Exercise 7.3.

Care: The geometric is parameterised so that $x$ is the number of failures before a success (not the number of trails). Similarly for the negative binomial.

sum( dbinom( 16:81,  # Part 1
             size = 81,
             prob = 0.20) ) # 0.5663638
#> [1] 0.5663638
sum( dbinom( 12:81,  # Part 2
             size = 81,
             prob = 0.20) ) # 0.9082294
#> [1] 0.9082294
  # Part 3
dgeom(x = 2, #i.e., two failures before first success
      prob = 0.20) # 0.128
#> [1] 0.128

  # Part 4
dnbinom(x = 5, # is 5 fails before 5th success
        prob = 0.20,
        size = 5) # 0.01321206
#> [1] 0.01321206
sum( dbinom(50:81,
            size = 81,
            prob = 0.2) )
#> [1] 3.042983e-16

Answer to Exercise 7.4.

dpois( 0,  # Part 1
       lambda = 3)
#> [1] 0.04978707
sum( dpois( 6:50,  # Part 2
            lambda = 3) )
#> [1] 0.08391794
dpois( 2,   # Part 3
       lambda = 6)
#> [1] 0.04461754

Answer to Exercise 7.5.

See Fig. E.33.

#> [1] 0.1252978
#> [1] 0.2424239
#> [1] 0.3401473
#> [1] 0.5232259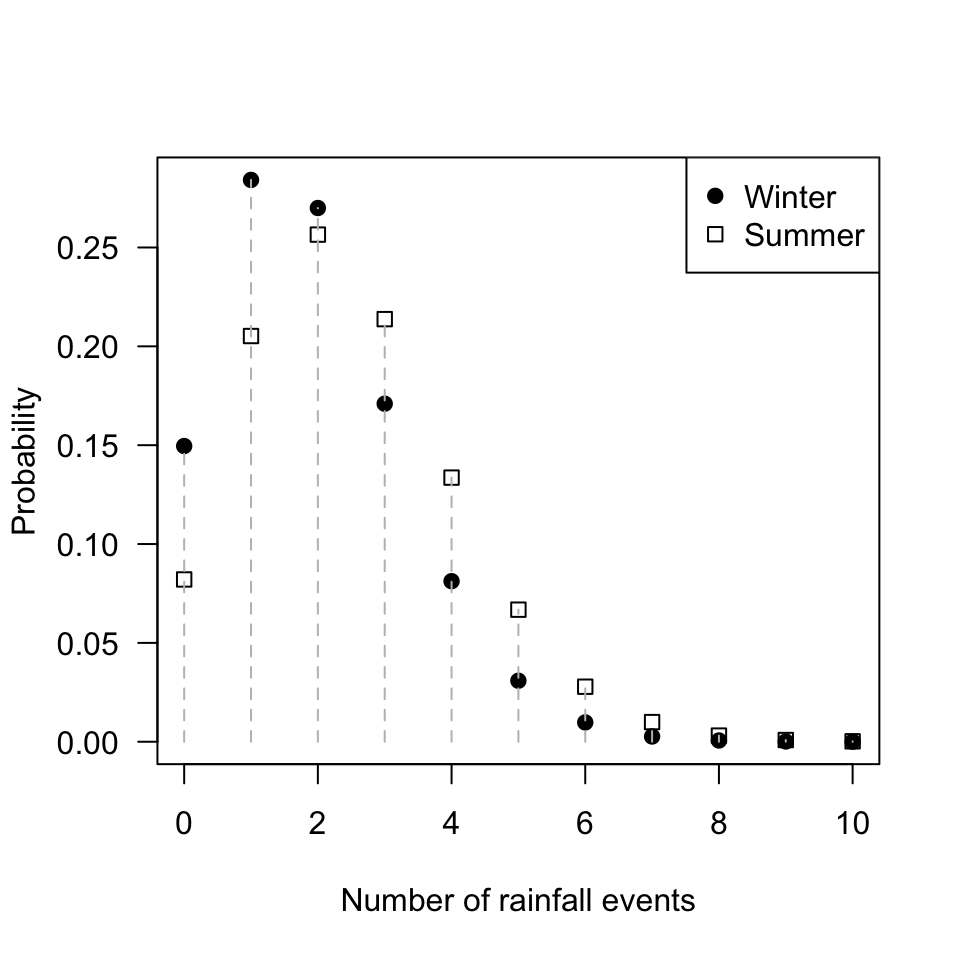

FIGURE E.33: The number of rainfall events in summer and winter

Answer to Exercise 7.6.

Yep.
$\log n_x = \log N + \log p + x\log (1 - p)$, which is a linear regression model of $\log n_x$ regressed on $x$, with intercept $\beta_0 = \log N + \log p$ and slope $\beta_1 = \log (1 - p)$.
So from the fitted slope, we can estimate $p$; then, using the estimated intercept, we can estimate $N$. More specifically, the estimate of $p$ is $1 - \exp( \hat{\beta}_1)$, and the estimate of $N$ is then $\exp(\beta_0 - \log p)$. We find $\hat{y} = 6.40525 - 1.128753x$. Then, the population size is estimate as about $894$: $p = 0.6765636$. $N = 894.2445$.

x <- 1:6
nx <- c(247, 63, 20, 4, 2, 1)

m1 <- lm( log(nx) ~ x); coef(m1)
#> (Intercept)           x 
#>    6.405250   -1.128753
beta0 <- coef(m1)[1]
beta1 <- coef(m1)[2]

p <- 1 - exp(beta1); p
#>         x 
#> 0.6765636
N <- exp(beta0 - log(p) ); N
#> (Intercept) 
#>    894.2445

Answer to Exercise 7.7 Defining $X$ as the ‘number of failures until $4$kWh/m² was observed’, since the parameterisation used in the textbook is for the number of failures until the first success.

Then, $X\sim \text{Geom}(p)$.

$\operatorname{E}(X) = (1 - p)/p = 1$ failures till first success, followed by the day of success: So 2.
$\operatorname{E}(X) = (1 - p)/p = 3$ failures, so $3 + 1 = 4$.
$\operatorname{var}(X) = (1 - p)/p^2 = 12$.

# Part 4
sum( dgeom(0:2,  # 0 to 2 failures before the success
           prob = 0.25))
#> [1] 0.578125

Answer to Exercise 7.13.

See Fig. E.34; not hugely different.
Similar probabilities: $0.85$ (in 1999) and $0.91$ (in 2000).
Similar: $16$ days (in 1999) and $12$ (in 2000).
Writing $X$ for the clutch size (where $n = 237$):
- $\operatorname{E}(X) = (1\times \frac{9}{237}) + (2\times \frac{29}{237}) + (3\times \frac{199}{237}) = 2.801688$, or about 2.8.
- $\operatorname{E}(X^2) = (1^2\times \frac{9}{237}) + (2^2\times \frac{29}{237}) + (3^2\times \frac{199}{237}) = 8.084388$.
- So, $\operatorname{var}(X) = 8.084388 - (2.801688)^2 = 0.2349324$, so the standard deviation is 0.4846982, or about 0.485.

  ## Part 2
1 -  pnbinom(30, mu = 23.0, size = 20.6) # 0.1416996
#> [1] 0.1416996
1 - pnbinom(30, mu = 19.5, size = 8.9) # 0.09175251
#> [1] 0.09175251
  ## Part 3
qnbinom(0.15, mu = 23.0, size = 20.6) # 16
#> [1] 16
qnbinom(0.15, mu = 19.5, size = 8.9)  # 12
#> [1] 12

x <- 0:50
y1999 <- dnbinom(x, mu = 23.0, size = 20.6)
y2000 <- dnbinom(x, mu = 19.5, size = 8.9)

plot( y1999 ~ x,
      pch = 19,
      las = 1,
      main = "Lay date for glaucous-winged gulls",
      xlab = "Lay date",
      ylab = "Prob. function")
points( y2000 ~ x,
        pch = 1)
legend("topleft",
       pch = c(19, 1),
       legend = c("1999",
                  "2000"))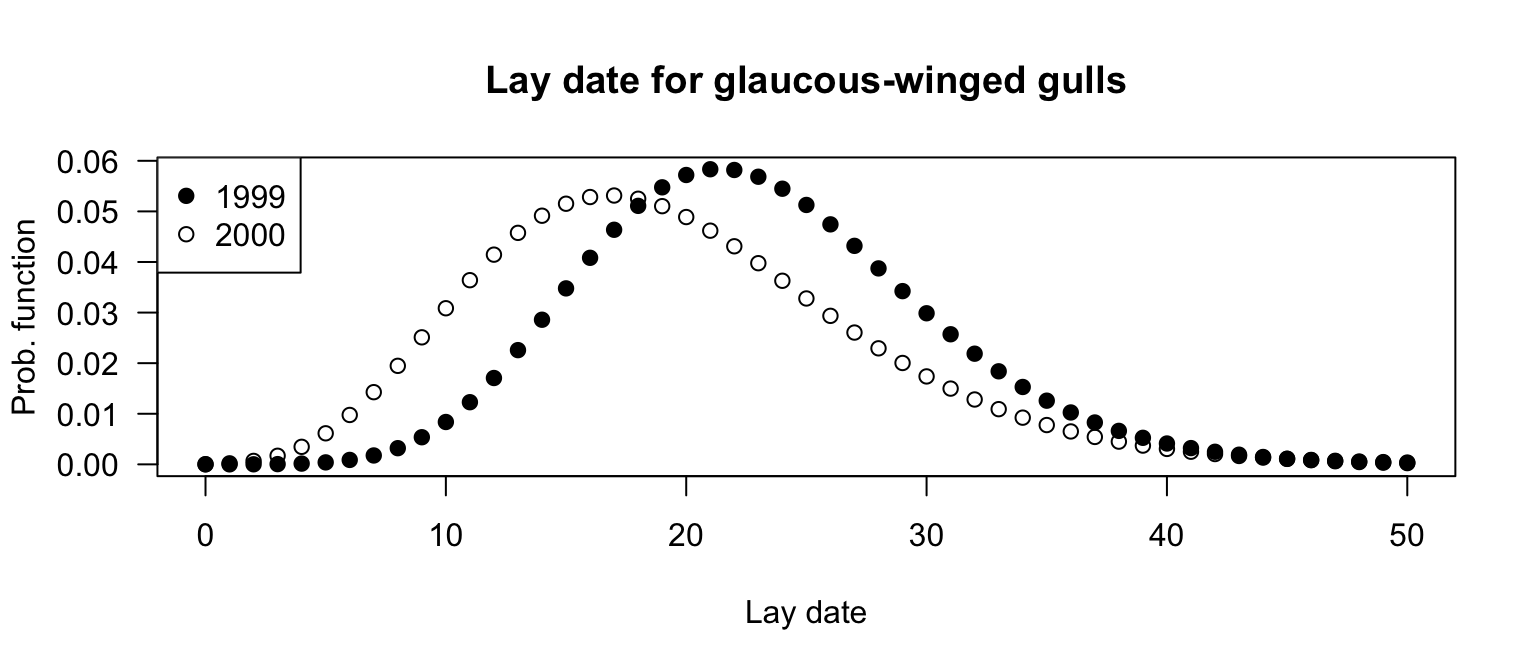

FIGURE E.34: The lay date model for glaucous-winged gulls, in 1999 and 2000

Answer to Exercise 7.14.

In Eq. (7.6), the rv $X$ refers to the number of failures before the $r$th success is observed, so that $X = 0, 1, 2, \dots$. So define $Y$ as the number of trials till the $r$th success, and hence $Y = X + r$.

The range space is $Y\in\{r, r + 1, r + 2, \dots\}$
$p_Y(y; p, r) = \binom{y - 1}{r - 1}(1 - p)^{y - r} p^{r - 1}$, for $y = r, r + 1, r + 2, \dots$.
$\operatorname{E}(Y) = \operatorname{E}(X + r) = \operatorname{E}(X) + r = r/p$.
$\operatorname{var}(Y) = \operatorname{var}(X + r) = \operatorname{var}(X) = r(1 - p)/p^2$.

Answer to Exercise 7.15.

Let $X$ be the number of typos per minute; then $X\sim\text{Pois}(\lambda = 2.5\times 5 = 12.5)$ for a five-minute test.

dpois(10, lambda = 12.5) # 0.09564364
#> [1] 0.09564364
dpois(6, lambda = 2.5 * 3) * dpois(4, lambda = 2.5 * 2) #  0.02398959
#> [1] 0.02398959

For Part 3: The number of errors occurring in the ‘overlap minute’ could be $0, 1, 2$, 6$. So proceed:

$6$ errors in overlap minute: $\Pr(\text{0 errors first 2 mins})\times{}$ $\Pr(\text{6 errors overlap min})\times{}$ $\Pr(\text{0 errors final 2 mins})$
$5$ errors in overlap minute: $\Pr(\text{1 error first 2 mins})\times{}$ $\Pr(\text{5 errors overlap min})\times{}$ $\Pr(\text{1 error final 2 mins})$

And so on.

prob <- function(ErrorsInOverlap){
  dpois( (6 - ErrorsInOverlap), lambda = 2 * 2.5) *
  dpois(ErrorsInOverlap, lambda = 1 * 2.5) *
  dpois((6 - ErrorsInOverlap), lambda = 2 * 2.5)
}
sum( prob( 0:6 ) ) # 0.02120811
#> [1] 0.02120811

Answer to Exercise 7.16.

$0.25$.
dbinom(x = 2, size = 4, prob = 0.25) ${}= 0.2109375$.

Answer to Exercise 7.17.

The code below is for one simulation for each part only.

### Part 1
set.seed(2268) # For reproducibility

queueLength <- array(dim = 60)

queueLength[1] <- rpois(1, lambda = 0.5)

for (i in 2:60){
   queueLength[i] <- queueLength[i - 1] + rpois(1, lambda = 0.5)
   # Print every 10 minutes
   if ( floor(i/10) == i/10 ) {
     cat("After ", i, " minutes past 8AM, queue length: ", queueLength[i], "\n")
   }
}
#> After  10  minutes past 8AM, queue length:  6 
#> After  20  minutes past 8AM, queue length:  14 
#> After  30  minutes past 8AM, queue length:  19 
#> After  40  minutes past 8AM, queue length:  24 
#> After  50  minutes past 8AM, queue length:  28 
#> After  60  minutes past 8AM, queue length:  34
plot( queueLength, type = "l", las = 1)

FIGURE E.35: A simulation




### Part 2
queuelength <- array(dim = 60)

queueLength[1] <- rpois(1, lambda = 0.5)

for (i in 2:60){
   NumberIn <- rpois(1, lambda = 0.5)

   # Number being served
   if ( i < 30 ) {
     NumberServed <- 0
   } else {
     if (i >= 30) {
        lambda <- 0.75
     }
     NumberServed <- rpois(1, lambda = lambda)
     queueLength[i] <- queueLength[i - 1] + NumberIn - NumberServed
   }

   if ( queueLength[i] < 0 ) queueLength[i] <- 0
}

plot( queueLength, type = "l", las = 1)
abline(v = 30,
       lwd = 2,
       col = "grey")
text(30, 5,
     pos = 3, # To the right,
     labels = "Server starts")

FIGURE E.36: A simulation





### Part 3.
queuelength <- array(dim = 60)

queueLength[1] <- rpois(1, lambda = 0.5)

for (i in 2:60){
   NumberIn <- rpois(1, lambda = 0.5)

   # Number being served
   if ( i < 30 ) {
     NumberServed <- 0
   } else {
     if ( (i > 30) & (i < 45) ) {
        lambda <- 0.7
     }
     if ( i > 45 ) {
        lambda <- 1.3
     }
     NumberServed <- rpois(1, lambda = lambda)
   }

   queueLength[i] <- queueLength[i - 1] + NumberIn - NumberServed

   if ( queueLength[i] < 0 ) queueLength[i] <- 0
}

plot( queueLength, type = "l", las = 1)
abline(v = 30,
       lwd = 2,
       col = "grey")
text(30, 5,
     pos = 3, # To the right,
     labels = "Server 1 starts")
abline(v = 45,
       lwd = 2,
       col = "grey")
text(45, 5,
     pos = 3, # To the right,
     labels = "Server 2 starts")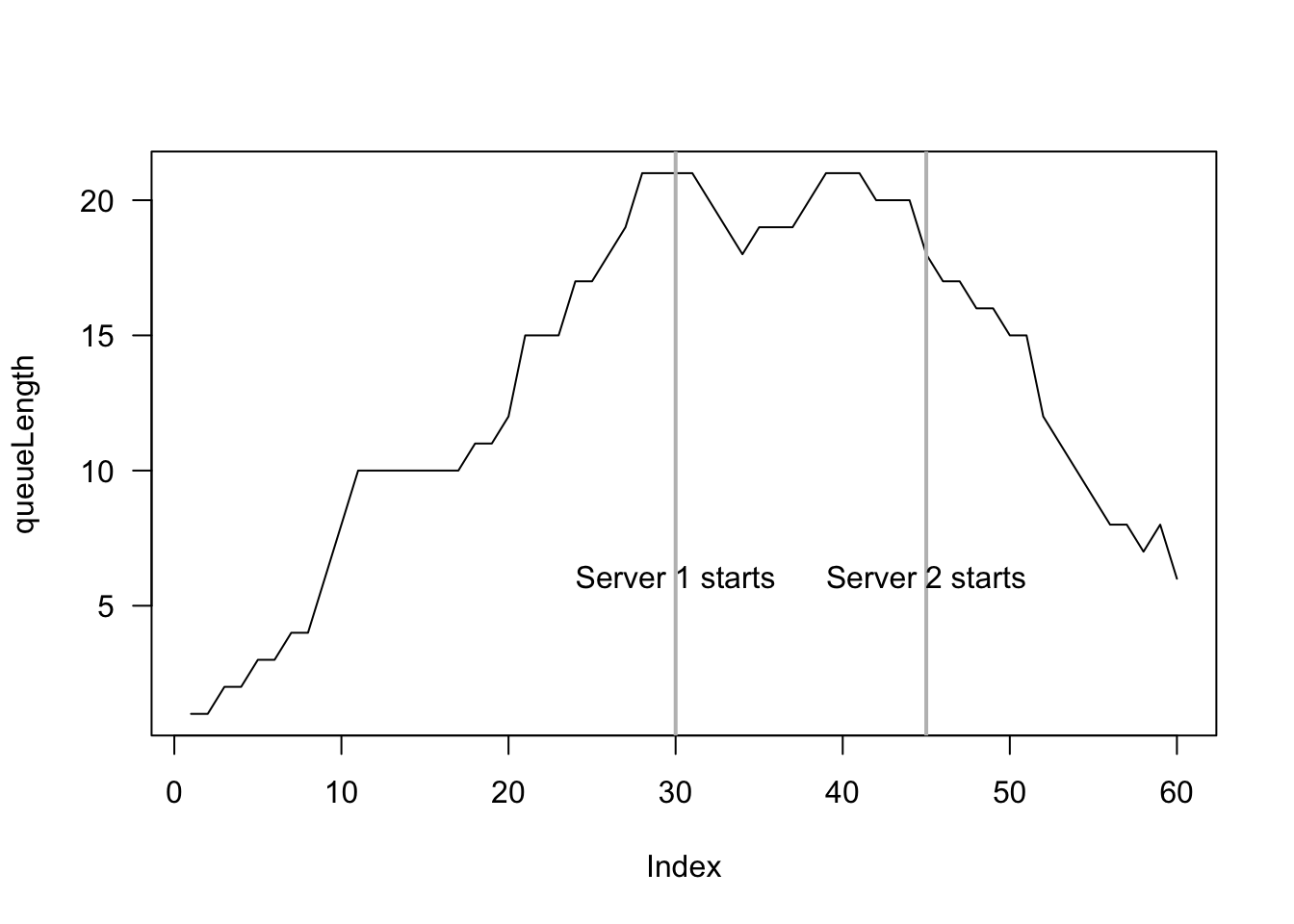

FIGURE E.37: A simulation

Answer to Exercise 7.18. Suppose $X\sim\text{Pois}(\lambda)$; then $\Pr(X) = \Pr(X + 1)$ implies \[\begin{align*} \frac{\exp(-\lambda)\lambda^x}{x!} &= \frac{\exp(-\lambda)\lambda^{x + 1}}{(x + 1)!} \\ \frac{\lambda^x}{x!} &= \frac{\lambda^{x} \lambda}{(x + 1) \times x!} \end{align*}\] so that $\lambda = x + 1$ (i.e., $\lambda$ must be a while number). For example, if $x = 4$ we would have $\lambda = 5$. And we can check:

dpois(x = 4,     lambda = 5)
#> [1] 0.1754674
dpois(x = 4 + 1, lambda = 5)
#> [1] 0.1754674

Answer to Exercise 7.19.

$\operatorname{E}(X) = kp$ which is the same as the binomial (here, $k$ is the sample size).
$\operatorname{var}(X) = k p (1 - p) \times \left(\frac{N - k}{N - 1}\right)$; the first bit is the variance for the binomial distribution (recall $k$$ is the sample size). The other term is $(N - k)/(N - 1)$, which is the FPC factor as defined.

Answer to Exercise 7.20.

Since $\operatorname{var}(Y) = \operatorname{E}(Y^2) - \operatorname{E}(Y)^2$, find $\operatorname{E}(Y^2)$ using (B.2):

\[\begin{align*} \operatorname{E}(Y^2) &= \sum_{i = 0}^{b - a} i^2\frac{1}{b - a + 1}\\ &= \frac{1}{b - a + 1}(0^2 + 1^2 + 2^2 + \dots +(b - a)^2)\\ &= \frac{1}{b - a + 1}\frac{(b - a)(b - a + 1)(2(b - a) + 1)}{6}\\ &= \frac{(b - a)(2(b - a) + 1)}{6}. \end{align*}\] Therefore \[\begin{align*} \operatorname{var}(X) = \operatorname{var}(Y) &= \frac{(b - a)(2(b - a) + 1)}{6} - \left(\frac{b - a}2\right)^2\\ &= \frac{(b - a)(b - a + 2)}{12}. \end{align*}\]

E.8 Answers for Chap. 8

Answer to Exercise 8.1.

For example: From $\mu = m/(m + n)$, we get $n = m(1 - \mu)/\mu$ and $m + n = m/\mu$. Also, from the expression for the variance, substitute $m + n = m/\mu$ and simplify to get \[ n = \frac{\sigma^2 m (m + \mu)}{\mu^3} \] Equate this expression for $n$ with $n = m(1 - \mu)/\mu$ from earlier, and solve for $m$. We get that $m = \frac{\mu}{\sigma^2}\left( \mu(1 - \mu) - \sigma^2\right)$; $n = \frac{1 - \mu}{\sigma^2}\left( \mu(1 - \mu) - \sigma^2\right)$.

Answer to Exercise 8.2.

$\operatorname{E}(X) = (72 + 30)/2 = 51$km.h^$-1$. $\operatorname{var}(X) = (72 - 30)^2 / 12 = 147$(km.h^$-1$)^$2$ (more easily understood, as $\sqrt{\operatorname{var}(X)} = 12.12$km.h^$-1$).
See Fig. E.38.
See below; $2/7 \approx 0.2857$.
See below; $7/12 \approx 0.5833$.

1 - punif(60, 30, 72)
#> [1] 0.2857143
(1 - punif(65, 30, 72) ) /
  (1 - punif(60, 30, 72) )
#> [1] 0.5833333

par(mfrow = c(1, 2))

x <- seq(10, 100,
         length = 1000)
plot( x = x,
      y = dunif(x, 
                min = 30,
                max = 72),
      type = "l",
      las = 1,
      xlab = "Vehicle speeds (in km/h)",
      ylab = "Probability density",
      main = "PDF for vehicle speeds")

x <- seq(10, 100,
         length = 1000)
plot( x = x,
      y = punif(x, 
                min = 30,
                max = 72),
      type = "l",
      las = 1,
      ylim = c(0, 1),
      xlab = "Vehicle speeds (in km/h)",
      ylab = "Probability density",
      main = "DF for vehicle speeds")

FIGURE E.38: Vehicle speeds

Answer to Exercise 8.3.

About $2.4$% of vehicles are excluded.
$Y$ has the distribution of $X \mid (X > 30 \cap X < 72)$ if $X \sim N(48, 8.8^2)$. The PDF is \[ f_Y(y) = \begin{cases} 0 & \text{for $y < 30$};\\ \displaystyle \frac{1}{8.8k \sqrt{2\pi}} \exp\left\{ -\frac{1}{2}\left( \frac{y - 48}{8.8}\right)^2 \right\} & \text{for $30\le y \le 72$};\\ 0 & \text{for $y > 72$}. \end{cases} \] where $k \approx \Phi(-2.045455) + (1 - \Phi(2.727273)) = 0.02359804$.

# Proportion excluded:
pnorm(30, 48, 8.8) + # Slower than 30
   (1- pnorm(72, 48, 8.8)) # Faster than 72
#> [1] 0.02359804

Answer to Exercise 8.4.

See Fig. E.39.
$\operatorname{E}(X) = \alpha \beta \approx 38.4$ and $\operatorname{var}(X) = \alpha \beta^2 \approx 54.54$, so standard deviation is about $7.38$.
$\Pr(C > 30 \mid C < 50) = \Pr(30 < C < 50) / \Pr(C < 50)\approx 0.870$.

alpha <- 27.05
beta <- 1.42

x <- seq(0, 80, length = 200)

par(mfrow = c(1, 2))

plot( y = dgamma(x, shape = alpha, scale = beta),
      x = x,
      las = 1,
      xlab = expression(italic(x)),
      ylab = "Prob. fn",
      type = "l",
      lwd = 2)
plot( y = pgamma(x, shape = alpha, scale = beta),
      x = x,
      xlab = expression(italic(x)),
      ylab = "Dist. fn",
      type = "l",
      las = 1,
      lwd = 2)

FIGURE E.39: The gamma distribution for the concrete diffusion model


( pgamma(50, shape = alpha, scale = beta) - 
  pgamma(30, shape = alpha, scale = beta) ) /
pgamma(50, shape = alpha, scale = beta)
#> [1] 0.8701039

Answer to Exercise 8.5.

See Fig. E.40.
About $0.0228$.
About $2.17$ kg/m^$3$.
About $2.21$ kg/m^$3$.

mn <- 2
sd <- 0.2

x <- seq(1.2, 2.8, length = 200)

par(mfrow = c(1, 2))

plot( y = dnorm(x, mean = mn, sd = sd),
      x = x,
      xlab = expression(italic(x)),
      ylab = "Prob. fn",
      type = "l",
      lwd = 2)
plot( y = pnorm(x, mean = mn, sd = sd ),
      x = x,
      xlab = expression(italic(x)),
      ylab = "Dist. fn",
      type = "l",
      lwd = 2)

FIGURE E.40: The gamma distribution for the surface chloride concentrations model


1 - pnorm(2.4, mean = mn, sd = sd)
#> [1] 0.02275013
qnorm(0.8, mean = mn, sd = sd)
#> [1] 2.168324
qnorm(0.85, mean = mn, sd = sd)
#> [1] 2.207287

Answer to Exercise 8.6.

See Fig. E.41.
$F_X(x) = \int_0^x ab t^{a - 1} (1 - t^a)^{b - 1} \, dt = 1 - (1 - x^a)^b$.
With $b = 1$, the PDF is $p_X(x) = a x^{a - 1}$. Also, \[\begin{align*} \text{Beta}(a, 1) &= \frac{x^{a - 1} (1 - x)^1 - 1}{B(a, 1)}\\ &= \frac{x^{a - 1} \Gamma(a + 1)}{\Gamma(a) \, \Gamma(a)} = a x^{a - 1}, \end{align*}\] which is the same as above.
With $a = b = 1$, the PDF is $p_X(x) = 1$, which is the continuous uniform distribution.
Write $Y = 1 - X$; then $p_X(x) = ab(1 - y)^{a - 1} (y^a) ^{b - 1}$.

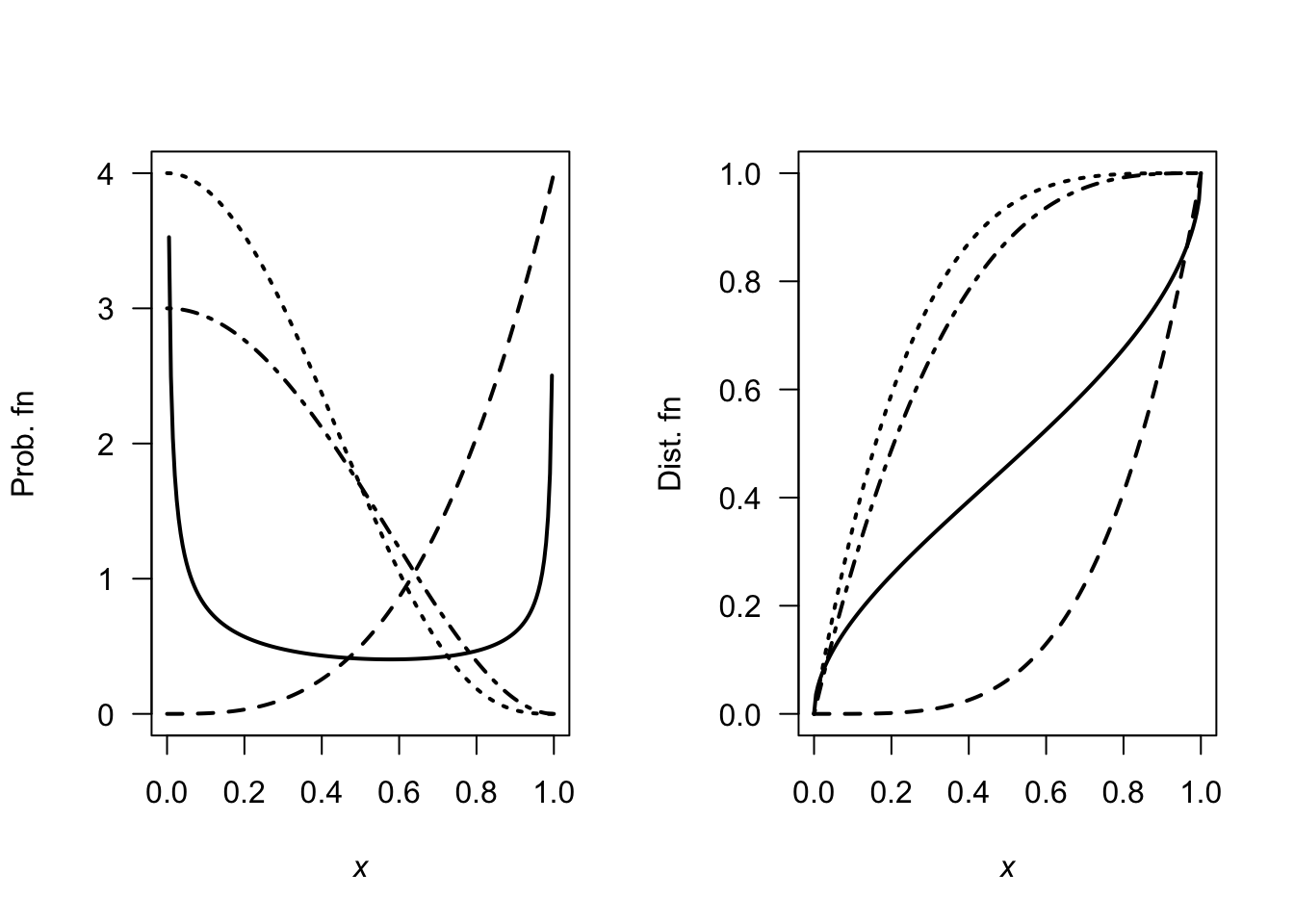
FIGURE E.41: Some Kumaraswamy distributions

Answer to Exercise 8.7.

$\text{CV} = \frac{\sqrt{a\beta^2}}{\alpha\beta} = 1/\sqrt{\alpha}$, which is constant.

Answer to Exercise 8.8.

For the given beta distribution, $\operatorname{E}(V) = 0.287/(0.287 + 0.926) = 0.2366...$ and $\operatorname{var}(V) = 0.08161874$.

$\operatorname{E}(S) = \operatorname{E}(4.5 + 11V) = 4.5 + 11\operatorname{E}(V) = 7.10$ minutes. $\operatorname{var}(S) = 11^2\times\operatorname{var}(V) = 9.875$ minutes².
See Fig. E.42.

v <- seq(0, 1, length = 500)

PDFv <- dbeta(v, shape1 = 0.287, shape2 = 0.926)

plot( PDFv ~ v,
      type = "l",
      las = 1,
      xlim = c(0, 1),
      ylim = c(0, 5),
      xlab = expression(italic(V)),
      ylab = "PDF",
      main = "Distribution of V",
      lwd = 2)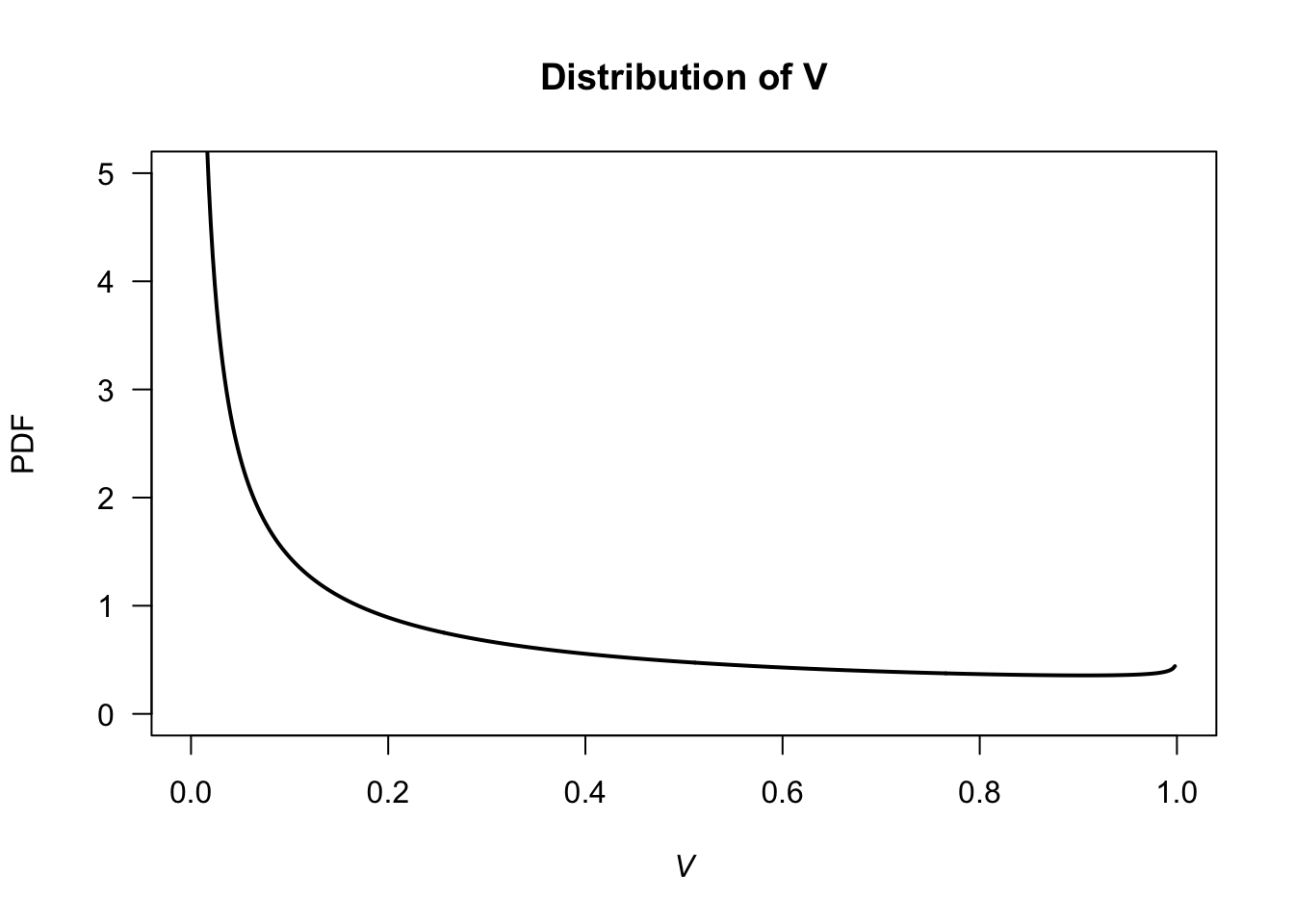

FIGURE E.42: Service times

Answer to Exercise 8.9.

$\operatorname{E}[T] = \operatorname{E}[0.5 + W] = 0.5 + \operatorname{E}[W] = 0.5 + 16.5 = 17.0$.
$\operatorname{var}[T] = \operatorname{var}[0.5 + W] = \operatorname{var}[W] = 16.5^2$, so the std dev is $16.5$.
$\Pr(T > 1) = \Pr( [W + 0.5] > 1 ) = \Pr(W > 0.5) = 0.9702$.

beta <- 16.5
x <- seq(0, 80, length = 1000)

yB <- dexp(x,
           rate = 1/beta)

plot( yB ~  x,
      las = 1,
      type = "l",
      ylim = c(0, 0.06),
      lwd = 2,
      main = expression(PDF~"for"~italic(W)),
      xlab = expression(italic(w)),
      ylab = "Prob. fn.")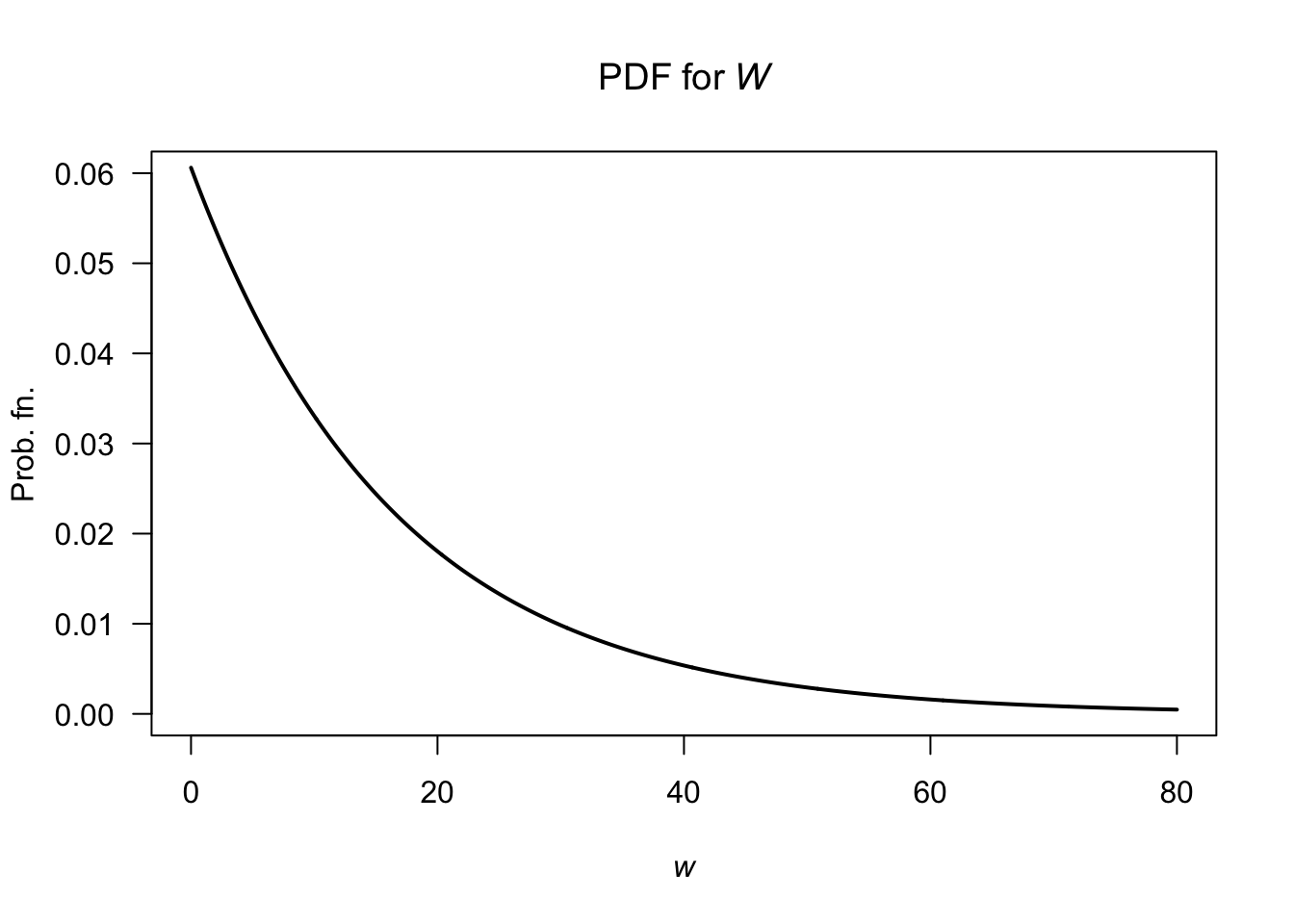

FIGURE E.43: Exponential distribution for hospitals


# Part 3
1 - pexp(0.5, rate = 1/beta) # 0.9701515
#> [1] 0.9701515

Answer to Exercise 8.12.

In summer: If the event lasts more than $1$ hour, what is the probability that it eventually lasts more than three hours?
In winter: If the event lasts more than $1$ hour, what is the probability that it lasts less than two hours?

alpha <- 2; betaS <- 0.04; betaW <- 0.03
x <- seq(0, 1, length = 1000)

yS <- dgamma( x, shape = alpha, scale = betaS)
yW <- dgamma( x, shape = alpha, scale = betaW)

plot( range(c(yS, yW)) ~  range(x),
      type = "n", # No plot, just canvas
      las = 1,
      xlab = "Event duration (in ??)",
      ylab = "Prob. fn.")
lines(yS ~ x, 
      lty = 1,
      lwd = 2)
lines(yW ~ x, 
      lty = 2,
      lwd = 2)
legend( "topright",
        lwd = 2,
        lty = 1:2,
        legend = c("Summer", "Winter"))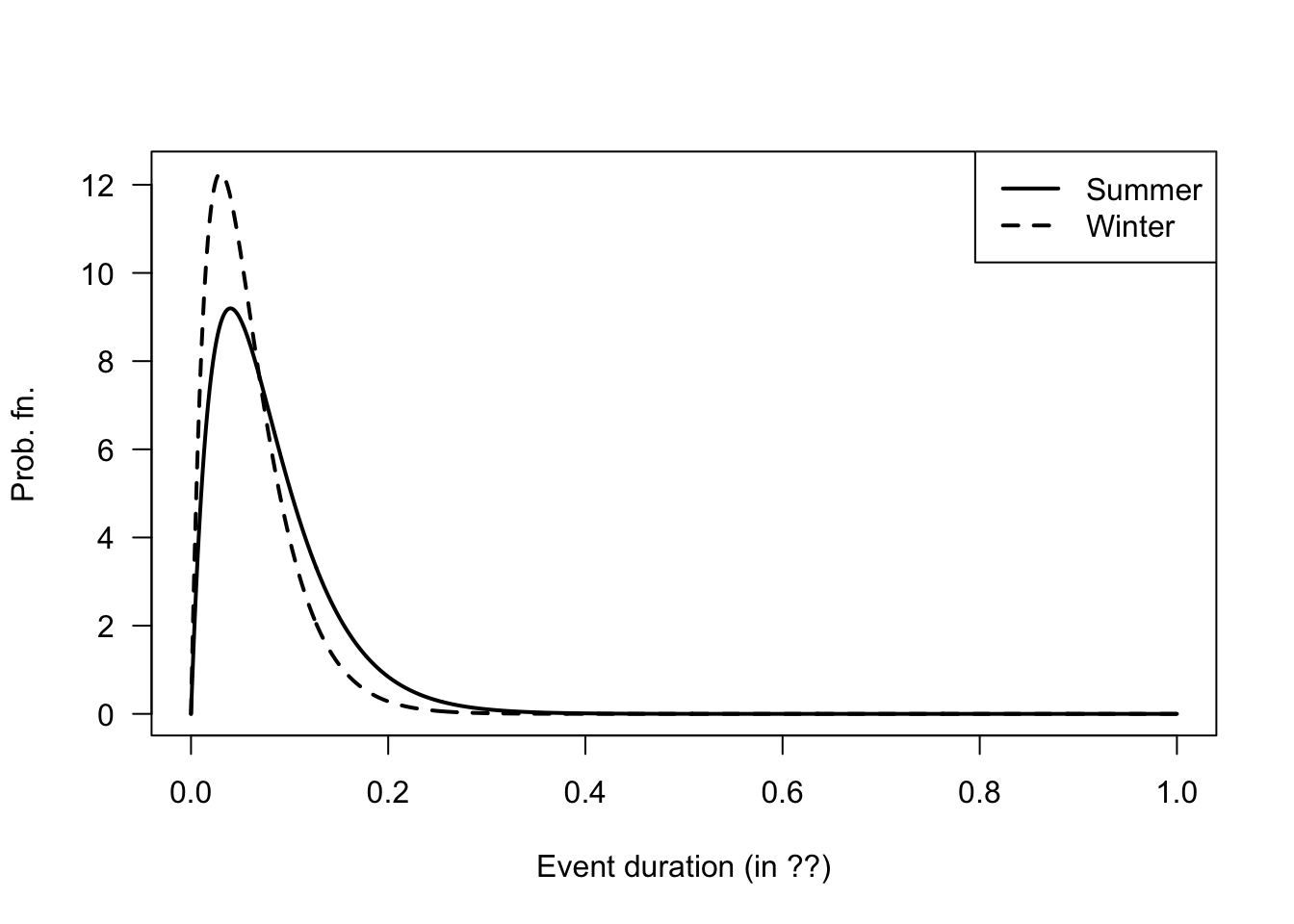

FIGURE E.44: Winter and summer

1 - pgamma(6/24, shape = alpha, scale = betaW)
#> [1] 0.002243448
1 - pgamma(6/24, shape = alpha, scale = betaS)
#> [1] 0.01399579

Answer to Exercise 8.14.

$\operatorname{E}(X) = \alpha\beta = 3.76$ days. $\operatorname{var}(X) = \alpha\beta^2 = 12.75$ days², so std dev is $3.571$ days.
The main difference is at the lower end of the distribution.
About $35%$ (gamma) and $31%$ (exponential).
Both just over $10$ days.

alpha <- 1.11; beta <- 3.39

x <- seq(0, 15, length = 500)
yGamma <- dgamma(x, shape = alpha, scale = beta)
yExp <- dexp(x, rate = 1/beta)

plot( range (c(yGamma, yExp)) ~ range(x),
      type = "n", # No plot, just canvas
      las = 1,
      xlab = "Duration of symptoms (in days)",
      ylab = "Prob. fn.")
lines( yGamma ~ x,
       lwd = 2,
       lty = 1)
lines( yExp ~ x,
       lwd = 2,
       lty = 2)
legend( "topright",
        lwd = 2,
        lty = 1:2,
        legend = c("Gamma", "Exponential"))

FIGURE E.45: Gamma and exponential


## Part 3
1 - pgamma(4, shape = alpha, scale = beta) # 0.3505492
#> [1] 0.3505492
1 - pexp(4, rate = 1/beta) # 0.3072969
#> [1] 0.3072969

## Part 4
qgamma(0.95, shape = alpha, scale = beta) # 10.86655
#> [1] 10.86655
qexp(0.95, rate = 1/beta) # 10.15553
#> [1] 10.15553

Answer to Exercise 8.15.

About $25.2$%.
$\Pr(T > 7 \mid T > 5) = \Pr(T > 7)/\Pr(T > 5)$ or about $33.8$%.
About $7$:$30$pm.

pnorm(5, mean = 6, sd = 1.5)
#> [1] 0.2524925

(1 - pnorm(7, mean = 6, sd = 1.5) ) /
  (1 - pnorm(5, mean = 6, sd = 1.5) )
#> [1] 0.3377793

qnorm(0.85, mean = 6, sd = 1.5)
#> [1] 7.55465

Answer to Exercise 8.16. Write $X$ for the percentage of clay content in soil.

For the two counties:

County A:
- $\operatorname{E}(X) = m / (m + n) = 0.708$ or about $70.8$%.
- $\operatorname{var}(X) = 0.01196957$ so the standard deviation is about $10.9$%.
County B:
- $\operatorname{E}(X) = m / (m + n) = 0.513$ or about $51.3$%.
- $\operatorname{var}(X) = 0.02939085$ so the standard deviation is about $17.0$%.

About $96$% for County A; about $53$% for County B. These look reasonable from the plots.

x <- seq(0, 1, length = 1000)
yA <- dbeta(x, shape1 = 11.52, shape2 = 4.75)
yB <- dbeta(x, shape1 = 3.85, shape2 = 3.65)

plot( range( c(yA, yB)) ~ range(100 * x),
      type = "n", #No plot, just canvas
      las = 1,
      xlab = "Percentage clay",
      ylab = "Prob. fn.")
lines( yA ~ I(100 * x),
       lwd = 2,
       lty = 1)
lines( yB ~ I(100 * x),
       lwd = 2,
       lty = 2)
legend("top",
       lty = 1:2,
       lwd = 2,
       legend = c("Location A", "Location B"))

FIGURE E.46: Clay content


## Part 3
qbeta( 0.5, shape1 = 11.52, shape2 = 4.75) #  0.7167495
#> [1] 0.7167495
qbeta( 0.5, shape1 = 3.85,  shape2 = 3.65) # 0.5145787
#> [1] 0.5145787

Answer to Exercise 8.20.

Note that if $Y = X - \Delta$, then $Y$ has a gamma distribution, with $\alpha = 2.5$ and $\beta = 0.8$, with $\operatorname{E}(Y) = \alpha\beta = 2$ and $\operatorname{var}(Y) = \alpha\beta^2 = 1.6$.

$\operatorname{E}(X) = \operatorname{E}(Y + \Delta) = 3.2$ seconds. $\operatorname{var}(X) = \operatorname{var}(Y) = 1.6$ seconds^$2$.

numSims <- 1000
yHeadway <- rgamma( n = numSims,
                    shape = 2.5,
                    rate = 0.8)
xHeadway <- yHeadway + 1.2
hist(xHeadway,
     las = 1,
     lwd = 2,
     xlim = c(0, max(xHeadway)),
     main = "Histogram of headway",
     ylab = "Prob. fn.",
     xlab = "Headway (in sec)")

FIGURE E.47: Headways


xMean <- 3.2; xVar <- 1.6
xLo <- 3.2 - 2 * sqrt(xVar)
xHi <- 3.2 + 2 * sqrt(xVar)
cat("Limits", xLo, "and", xHi, "\n")
#> Limits 0.6701779 and 5.729822

# Part 3
Num <- sum( (xHeadway < xHi ) & (xHeadway > xLo) )
EmpiricalProp <- Num / numSims
EmpiricalProp
#> [1] 0.766

# Part 4: Tchebyshev: AT LEAST this proportion
k <- 2
1 - 1/k^2
#> [1] 0.75

Answer to Exercise 8.23.

htMean <- function(x) {
  7.5 * x + 70
}
htSD <- function(x) {
  0.4575 * x + 1.515
}

NumSims <- 10000

Ages <- c(
  rep(2, NumSims * 0.32),
  rep(3, NumSims * 0.33),
  rep(4, NumSims * 0.25),
  rep(5, NumSims * 0.10)
)

Hts <- rnorm(NumSims,
             mean = htMean(Ages),
             sd = htSD(Ages))
hist(Hts,
     las = 1,
     xlab = "Heights (in cm)")

FIGURE E.48: Heights of children at day-care facilities


# Taller than 100:
cat("Taller than 100cm:", sum( Hts > 100) / NumSims * 100, "%\n")
#> Taller than 100cm: 22.42 %
# Mean and variance:
cat("Mean:", mean( Hts ), "cm; ",
    "Std dev: ", sd(Hts), "cm\n")
#> Mean: 93.52505 cm;  Std dev:  7.936301 cm

# Sort the heights to find where the tallest 20% are:
cat("Tallest 15% are taller than", 
    sort(Hts)[ NumSims * 0.85], "cm\n")
#> Tallest 15% are taller than 102.545 cm

Answer to Exercise 8.24. Normal: $\operatorname{var}(X) = \sigma^2 \mu^0$, so $\phi = \sigma^2$ and $p = 0$.

Poisson: $\operatorname{var}(X) = \mu$, so $\phi = 1$ and $p = 1$.

Gamma: $\operatorname{var}(X) = \phi \mu^2$, so $\phi = ???$ and $p = 2$.

E.9 Answers for Chap. 9

Answer to Exercise 9.1.

Answer to Exercise 9.2.

Answer to Exercise 9.3. 1. We have \[ \Pr(Y < 0) = \Pr\big(Z < (0 - 1.5)/1\big) = \Phi(-1.5) \approx 0.0668, \] using $Z$ as a standard normal variate (Sect. 8.3.2). 2. To use the functions $\Phi(\cdot)$ and $\phi(\cdot)$, the standardised version of $Y$ must be used; that is, $Z = (Y - 1.5)/1 = (Y - 1.5)$ in these functions. Then, \[ f_X(x) = \begin{cases} 0 & \text{if $X < 0$};\\ \Phi(-1.5) & \text{if $X = 0$};\\ \phi(x - 1.5) & \text{if $X > 0$}, \end{cases} \] From Equation (9.1), \[ f_{X\mid X > 0}(x) = \frac{\phi(x- 1.5)}{1 - \Phi(-1.5)} \approx 1.148\dots \times \phi(x) \] for $X > 0$. From this expression, \[\begin{align*} \operatorname{E}[X] = \operatorname{E}[X \mid X>0] &= \int_0^\infty ???\,dx \\ & \text{FIX!} \end{align*}\] Similarly, \[ \operatorname{var}[X] = \operatorname{var}[X \mid X>0] = ??? \] 3. See Fig. E.49.

FIGURE E.49: A censored model, using a normal distribution for the continuous component, with the threshold value at $X = 0$.

E.10 Answers for Chap. 10

E.11 Answers for Chap. 11

Answer to Exercise 11.1. 1. $\operatorname{E}(\overline{X}) = \operatorname{E}([X_1 + X_2 + \cdots + X_n]/n) = [\operatorname{E}(X_1) + \operatorname{E}(X_2) + \cdots + \operatorname{E}(+ X_n)]/n = [n \mu]/n = \mu$. 2. $\operatorname{var}(\overline{X}) = \operatorname{var}([X_1 + X_2 + \cdots + X_n]/n) = [\operatorname{var}(X_1) + \operatorname{var}(X_2) + \cdots + \operatorname{var}(X_n)]/n^2 = [n \sigma^2]/n^2 = \sigma^2/n$.

Answer to Exercise 11.2.

For one month:

set.seed(932649)

NumRainEvents <- rpois(1,
                       lambda = 0.78)
MonthlyRain <- 0

if ( NumRainEvents > 0) {
     EventAmounts <- rgamma(NumRainEvents,
                           shape = 0.5,
                           scale = 6 )
     MonthlyRain <- sum( EventAmounts )
}

For $1000$ simulations:

set.seed(932649)

MonthlyRain <- array(0,  
                     dim = 1000)

for (i in 1:1000){
 NumRainEvents <- rpois(1,
                       lambda = 0.78)
 MonthlyRain[i] <- 0

  if ( NumRainEvents > 0) {
       EventAmounts <- rgamma(NumRainEvents,
                             shape = 0.5,
                             scale = 6 )
       MonthlyRain[i] <- sum( EventAmounts )
  }
}

# Exact zeros:
sum(MonthlyRain == 0) / 1000
#> [1] 0.484
mean(MonthlyRain)
#> [1] 2.196798
mean(MonthlyRain[MonthlyRain > 0])
#> [1] 4.25736

Answer to Exercise 11.3.

$\operatorname{E}[U] = \mu_x - \mu_Z$; $\operatorname{E}[V] = \mu_x - 2\mu_Y + \mu_Z$.
$\operatorname{var}[U] = \sigma^2_x + \sigma^2_Z$; $\operatorname{E}[V] = \sigma^2_x + 4\sigma^2_Y + \sigma^2_Z$.
Care is needed! \[\begin{align*} \text{Cov}[U, V] &= \operatorname{E}[UV] - \operatorname{E}[U]\operatorname{E}[V]\\ &= \operatorname{E}[X^2 - 2XY + XZ - XZ + 2YZ - Z^2] - \\ &\qquad (\mu_X^2 + 2\mu_X\mu_Y + \mu_X\mu_Z - \mu_X\mu_Z - 2\mu_Y\mu_Z - \mu^2_z)\\ &= (\operatorname{E}[X^2] - \mu_X^2) - 2(\operatorname{E}[XY] - \operatorname{E}[X]\operatorname{E}[Y]) + 2(\operatorname{E}[YZ] - \mu_Y\mu_Z) -\\ &\qquad (\operatorname{E}[Z^2] - \mu_Z^2)\\ &= \sigma^2_X - \sigma^2_Z, \end{align*}\] since the two middle terms become $-2\text{Cov}[X, Y] + 2\text{Cov}[Y, Z]$, are both are zero (as given).
The covariance is zero if $\sigma^2_X = \sigma^2_Z$.

Answer to Exercise 11.4.

First, $\Pr(X \mid Y = 2) = |x - 2|/11$. Then, the marginal distribution is \[ p(X\mid Y = 2) = \begin{cases} 2/3 & \text{for $x = 0$};\\ 1/3 & \text{for $x = 1$.} \end{cases} \] So $\operatorname{E}(X \mid Y = 2) = 1/3$.
First, $p_X(x) = \frac{1}{11}( |x - 1| + |x - 2| + |x - 3|)$ for $x = 0, 1, 2$; so $\Pr(X\ge 1) = 5/11$. The probability function is non-zero for $y = 1, 2, 3$. Then \[ p(Y\mid x\ge 1) = \begin{cases} 1/5 & \text{for $y = 1$};\\ 1/5 & \text{for $y = 2$};\\ 3/5 & \text{for $y = 3$}. \end{cases} \] Then, $\operatorname{E}(Y \mid X\ge 1) = 12/5$.

Answer to Exercise 11.5.

We find $f_X(x) = 1$ for $0 < x < 1$ and $f_Y(y) = 1$ for $0 < y < 1$.
We need some intermediate values:
- $\operatorname{E}(X) = \operatorname{E}(Y) = 1/2$;
- $\operatorname{var}(X) = \operatorname{var}(Y) = 1/12$;
- $\operatorname{E}(XY) = (9 - \alpha)/36$.
Then $\text{Cov}(X, Y) = -\alpha/36$ and so $\text{Cor}(X, Y) = -\alpha/3$.
Independence if $f_X(x) \times f_Y(y) = f_{XY}(x, y)$, which occurs only when $\alpha = 0$.
$\Pr(X < Y) = \int_0^1\!\!\int_y^1 1 - \alpha(1 - 2x)(1 - 2y)\, dx\, dy = 1/2$.

Answer to Exercise 11.9.

For an exponential distribution, the MGF is $M_X(t) = (1 - \beta t)^{-1}$. Now, the MGF is a sum is the product of the MGFs (see Theorem 5.6), so the MGF of $W = Z_1 + Z_2 + \cdots + Z_n$ is \[ M_W(t) = \prod_{i = 1}^n (1 - \beta t)^{-1} = (1 - \beta t)^{-n}, \] which is the MGF of a gamma distribution with parameters $n$ and $\beta$, as to be shown.

Answer to Exercise 11.11.

Adding: \[ p_X(x) = \begin{cases} 0.40 & \text{for $x = 0$};\\ 0.45 & \text{for $x = 1$};\\ 0.15 & \text{for $x = 3$}. \end{cases} \]
$\Pr(X \ne Y) = 1 - \Pr(X = Y) = 1 - (0.20) = 0.80$.
$X < Y$ only includes these five $(x, y)$ elements of the sample space: $\{ (0, 1), (0, 2), (0, 3); (1, 2), (1, 3)\}$. The sum of these probabilities is $0.65$.

Then, given these five, only two of them sum to three (i.e., $(0, 3)$ and $(1, 2)$). So the probability of the intersection is $\Pr( \{0, 3\} ) + \Pr( \{1, 2\}) = 0.30$. So the conditional probability is $0.30/0.65 = 0.4615385$, or about $46$%.
No: For $X = 0$, the values of $Y$ with non-zero probability are $Y = 1, 2, 3$. However, for $X = 1$ (for example), the values of $Y$ with non-zero probability are $Y = 1, 2$.

Answer to Exercise 11.14. 1. $f(x_1, x_2, \dots, x_n) = 4^n \prod_{i = 1}^n x_i^3$. 2. $\Pr(X_1 < 1/2) = \int_0^{1/2} 4 x^3 \, dx = 1/16 = 0.0625$. 3. The prob. is $16^{-n}$. 4. Same as 3.

Answer to Exercise 11.16.

A table can be used to show the sample space (below). Looking for $X = 4$ we deduce that \[ p_Y(y|X = 4) = \begin{cases} 2/7 = 0.2857 & \text{for $y = 1$};\\ 2/7 & \text{for $y = 2$};\\ 2/7 & \text{for $y = 3$};\\ 1/7 & \text{for $y = 4$};\\ 0 & \text{elsewhere}.\\ \end{cases} \] Hence we deduce that $\operatorname{E}[Y | X = 4] = 16/7\approx 2.2857$.

The table shows the values of $(x, y)$ (that is, the table entries are $(\text{max}, \text{min})$).

.	Die 1: 1	2	3	4	5	6
Die 2: 1	$(1, 1)$	$(2, 1)$	$(3, 1)$	$(4, 1)$	$(5, 1)$	$(6, 1)$
2	$(2, 1)$	$(2, 2)$	$(3, 2)$	$(4, 2)$	$(5, 2)$	$(6, 2)$
3	$(3, 1)$	$(3, 2)$	$(3, 3)$	$(4, 3)$	$(5, 3)$	$(6, 3)$
4	$(4, 1)$	$(4, 2)$	$(4, 3)$	$(4, 4)$	$(5, 4)$	$(6, 4)$
5	$(5, 1)$	$(5, 2)$	$(5, 3)$	$(5, 4)$	$(5, 5)$	$(6, 5)$
6	$(6, 1)$	$(6, 2)$	$(6, 3)$	$(6, 4)$	$(6, 5)$	$(6, 6)$

#> [1] 2.301363

Answer to Exercise 11.18.

annualRainfallList <- array( NA, dim = 1000)
for (i in 1:1000){
   rainAmounts <- array( 0, dim = 365) # Reset for each simulation

    wetDays <- rbinom(365, size = 1, prob = 0.32) # 1: Wet day
   locateWetDays <- which( wetDays == 1 )


   rainAmounts[locateWetDays] <- rgamma( n = length(locateWetDays),
                                         shape = 2,
                                         scale = 20)
   annualRainfallList[i] <- sum(rainAmounts)
}
# hist( annualRainfallList)

Days <- 1 : 365
prob <- (1 + cos( 2 * pi * Days/365) ) / 2.2

annualRainfallList2 <- array( NA, dim = 1000)
for (i in 1:1000){

  wetDays <- rbinom(365, size = 1, prob = prob) # 1: Wet day
  
  locateWetDays <- which( wetDays == 1 )
  
  rainAmounts2 <- array( 0, dim = 365)
  
  rainAmounts2[locateWetDays] <- rgamma( n = length(locateWetDays),
                                         shape = 2,
                                         scale = 20)
   annualRainfallList2[i] <- sum(rainAmounts2)
}
#hist( annualRainfallList2)

Days <- 1 : 365

probList <- array( dim = 365)
probList[1] <- 0.32

annualRainfallList3 <- array( NA, dim = 1000)

for (i in 1:1000){
  
  rainAmounts <- array( dim = 365 )

  for (day in 1:365) {
    if ( day == 1 ) {
      probList[1] <- 0.32
      wetDay <- rbinom(1, 
                       size = 1, 
                       prob = probList[1]) # 1: Wet day
      rainAmounts[1] <- rgamma( n = 1,
                                shape = 2,
                                scale = 20)

    } else {
    
      probList[i] <- ifelse( rainAmounts[day - 1] == 0,
                             0.15,
                             0.55)
      wetDay <- rbinom(1, 
                       size = 1, 
                       prob = probList[i]) # 1: Wet day

      if (wetDay) {
        rainAmounts[day] <- rgamma( n = 1,
                                    shape = 2,
                                    scale = 20)
      } else {
        rainAmounts[day] <- 0
      }
    }
  }
  annualRainfallList3[i] <- sum(rainAmounts)
    
}

#hist( annualRainfallList3)

Answer to Exercise 11.19.

Since $X + Y + Z = 500$, once the values of $X$ and $Y$ are known, the value of $Z$ has one specific value (i.e., all three values are not free to vary).
See Fig. E.50 (left panel).
See Fig. E.50 (right panel).
Proceed: \[\begin{align*} 1 &= \int_{200}^{300} \!\! \int_{100}^{400 - y} k\,dx\,dy + \int_{100}^{200} \!\! \int_{300 - y}^{400 - y} k\,dx\,dy \\ &= 30\ 000, \end{align*}\] so that $k = 1/30\,000$.

FIGURE E.50: The sample space for the mixture of nuts and dried fruit

Answer for Exercise 11.20.

Let $W$, $A$, and $P$ denote the walnut, almond, and peanut weights (in grams). Since each packet contains $250\,\text{g}$: \[ W + A + P = 250 \quad \Rightarrow \quad P = 250 - W - A. \] Once $W$ and $A$ are specified, $P$ is determined.
We have $W \ge 0$, $A \ge 0$ and $0 \le P \le 100$. Then, since $P = 250 - W - A$, \[ 0 \le 250 - W - A \le 100 \quad \Rightarrow \quad 150 \le W + A \le 250. \] Hence the sample space is \[ \mathcal{R}_2 = \{(w,a) : w \ge 0, \; a \ge 0, \; 150 \le w + a \le 250\}. \] This is a trapezoid in the $(W, A)$-plane with vertices \[ (150, 0), \quad (250, 0), \quad (0, 250), \quad (0, 150). \]
Adding the requirements $W \ge 25$ and $A \ge 25$ gives the feasible region as \[ \mathcal{R}_3 = \{(w,a) : w \ge 25, \; a \ge 25, \; 150 \le w + a \le 250\} \] with corners at \[ (125, 25), \quad (225, 25), \quad (25, 225), \quad (25, 125). \]
Assuming the weights are uniformly distributed over the feasible region with just the peanuts restriction, the area is \[ \text{Area}(\mathcal{R}_2) = \frac{1}{2}\cdot 250^2 - \frac{1}{2}\cdot 150^2 = 20\,000. \] So \[ f_{W, A}(w, a) = \begin{cases} \frac{1}{20\,000} & (w, a) \in \mathcal{R}_2, \\[6pt] 0 & \text{otherwise}. \end{cases} \] Then, with additional lower bounds, we can shift variables: $u = w - 25$ and $v = a - 25$. Then $u, v \ge 0$ and $100 \le u + v \le 200$. Thus \[ \text{Area}(\mathcal{R}_3) = \frac{1}{2}\cdot 200^2 - \frac{1}{2}\cdot 100^2 = 15\,000. \] So \[ f_{W, A}(w, a) = \begin{cases} \frac{1}{15\,000} & (w, a) \in \mathcal{R}_3, \\[6pt] 0 & \text{otherwise}. \end{cases} \] Note that in both cases $P = 250 - W - A$, so the joint distribution of $(W, A, P)$ is uniform over the feasible $2$-dimensional region \[ \{(w, a, p): w + a + p = 250, \; (w, a)\in \mathcal{R}_2 \text{ or } \mathcal{R}_3\}. \]

Answer to Exercise 11.21.

Joint density–-mass. For $y\in\{0, 1\}$, \[ f_{X, Y}(x, y) = f_{X\mid Y}(x\mid y)\,p_Y(y) = \begin{cases} \displaystyle \phi(x; \mu_1 = 8,\sigma_1^2 = 1)\cdot 0.10, & y = 1,\\[4pt] \displaystyle \phi(x; \mu_0 = 5,\sigma_0^2 = 1)\cdot 0.90, & y = 0, \end{cases} \] where $\phi(x; \mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\, \sigma} \exp\!\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)$.
Marginal density of $X$. This is a mixture of two normals: \[ f_X(x) = \sum_{y\in\{0, 1\}} f_{X\mid Y}(x\mid y)\,p_Y(y) = 0.10\,\phi(x; 8, 1) + 0.90\,\phi(x; 5, 1). \]
Posterior $\Pr(Y = 1\mid X = 7)$. By Bayes’ rule with densities, \[ \Pr(Y = 1\mid X = 7) = \frac{f_{X\mid Y}(7\mid 1)\,p_Y(1)}{f_X(7)} = \frac{0.10\,\phi(7; 8, 1)}{0.10\,\phi(7; 8, 1) + 0.90\,\phi(7; 5, 1)}. \] Numerically, \[ \phi(7; 8, 1) = 0.2419707245,\quad \phi(7; 5, 1) = 0.0539909665, \] so \[ f_X(7) = 0.10 (0.2419707245) + 0.90 (0.0539909665) = 0.0727889423, \] and \[ \Pr(Y = 1\mid X = 7) = \frac{0.0241970725}{0.0727889423} \approx 0.3324. \]
Given a biomarker value of $7$ mmol.L^$-1$, the estimated probability the patient has the disease is about 33% under this model ($10$% prevalence and the specified conditional normal distributions).

Answer to Exercise 11.22.

Joint density–-mass.
Let $p_Y(1) = 0.5$, $p_Y(2) = 0.3$, $p_Y(3) = 0.2$, and \[ X\mid Y = y \sim \mathrm{Exp}(\lambda_y), \quad \lambda_1 = 1,\ \lambda_2 = 0.5,\ \lambda_3 = 0.25. \] Then for $x\ge 0$, \[ f_{X, Y}(x,y) = p_Y(y)\, f_{X\mid Y}(x\mid y) = p_Y(y)\,\lambda_y e^{-\lambda_y x}. \]
Marginal density of $X$.
Mixture of exponentials: \[ f_X(x) = \sum_{y = 1}^3 p_Y(y)\,\lambda_y e^{-\lambda_y x} = 0.5\,e^{-x} + 0.15\,e^{-0.5x} + 0.05\,e^{-0.25x}, \quad x\ge 0. \]
$\Pr(Y = 1\mid X\le 2)$. Use Bayes’ rule for events: \[ \Pr(Y = 1\mid X\le 2) = \frac{\Pr(Y = 1, X\le 2)}{\Pr(X\le 2)} = \frac{p_Y(1)\,\Pr(X\le 2\mid Y = 1)}{\sum_{y = 1}^3 p_Y(y)\,\Pr(X\le 2\mid Y = y)}. \] For an exponential, $\Pr(X\le t\mid Y = y) = 1 - e^{-\lambda_y t}$. Thus, \[ \Pr(Y = 1, X\le 2) = 0.5\,(1-e^{-2}) = 0.4323323584, \] \[ \Pr(X\le 2) = 0.5(1 - e^{-2}) + 0.3(1 - e^{-1}) + 0.2(1 - e^{-0.5}) = 0.7006623941. \] Therefore, \[ \Pr(Y = 1\mid X\le 2) = \frac{0.4323323584}{0.7006623941} \approx 0.6170. \]
Interpretation. Given that the component failed within $200$ hours, the most likely mode is mechanical; the posterior probability is about $62$%, higher than its prior $50$% because the mechanical mode has the shortest expected lifetime (largest rate).

Answer for Exercise 3.28.

$a = 1/3$.
We find: \[ F_Y(y) = \begin{cases} 0. & \text{for $t < 0$};\\ 1/3 & \text{for $t = 0$};\\ (1 - t + 3t^2 - t^3)/3 & \text{for $0 < t < 2$};\\ 1 & \text{for $t \ge 2$}. \end{cases} \]

E.12 Answers for Chap. 12

Answer to Exercise 12.3.

$\operatorname{E}(Y) = \int_0^1 y(3y^2)\, dy = 3/4$. $\operatorname{E}(Y^2) = 3/5$, so $\operatorname{var}(Y) = 3/80$. By the CLT, $\overline{Y}\sim N(3/4, 3/(80n) )$. Therefore \[ \Pr\left( 3/4 - \sqrt{3/80} < \overline{Y} < 3/4 + \sqrt{3/80} \right) = \Pr\left( 0.56 < \overline{Y} < 0.94 \right) \] is needed. For a sample of size $n$,
\[ \Pr\left( \frac{0.56 - 0.75}{0.19/\sqrt{n}} < Z < \frac{0.56 - 0.75}{0.19/\sqrt{n}} \right) = \Pr(-\sqrt{n} < Z < \sqrt{n} ) \] which approaches one as $n\to\infty$. For example, if $n = 10$, $\Pr(-\sqrt{10} < Z < \sqrt{10} ) = 0.9984$.

Answer to Exercise 12.4.

Let the weight be $E$, so $E\sim N(59, 0.7)$. By the CLT, the sample mean $\overline{E} \sim N(59, 0.7/20)$. So \[ \Pr(\overline{E} > 59.5) = \Pr(Z > \frac{59.5 - 59}{\sqrt{0.7/20}}) = \Pr(z > 2.67) \approx 0.003792562. \] 1. We seek $\Pr(s^2 > 1)$. Since \[ \frac{(n - 1)s^2}{\sigma^2}\sim \chi^2_{n - 1} \] where $n = 12$ and $\sigma^2 = 0.7$. So \[\begin{align*} \Pr(s^2 > 1) &= \Pr\left( \frac{11 s^2}{0.7} > \frac{11\times 1}{0.7} \right)\\ &=\Pr( \chi^2_{11} > 15.714)\\ &\approx 0.152. \end{align*}\]

Answer to Exercise 12.5.

Let the number broken be $B$, so $B \sim \text{Pois}(0.2)$.

The sample mean number (with $n = 20$) broken has the distribution $\overline{B}\sim N(0.2, 0.2/20)$ approx. So \[ \Pr(B\ge 1) = \Pr\left( Z > \frac{1 - 0.2}{\sqrt{0.2/20}} \right) = \Pr(Z > 8) = 0. \]
In contrast, in any single carton, the probability of more than one broken egg is \[ \Pr(B > 1) = 1 - \Pr(B = 0) = 1 - 0.8187 = 0.181 \] using the Poisson distribution.

Answer to Exercise 12.6.

$\operatorname{E}(M) = 3/4$.
$\operatorname{var}(M) = 3/80$.
$\overline{M}\sim N(3/4, 1/240)$.
$0.8788$.

E.13 Answers for Chap. 13

Answer to Exercise 13.1. Compare the density function in Eq. (13.1) to the beta distribution density function.

Answer to Exercise 13.2. Compare the expressions for $\operatorname{E}[X]$ and $\operatorname{E}[X^2]$ to the beta distribution density function.

Answer to Exercise 13.3. $\displaystyle \frac{n!}{(k - 1)!\,(n - k)!} \frac{(x + 1)^{k - 1} (1 - x)^{n - k}}{2^n}$ for $-1\le x\le 1$.

Answer to Exercise 13.4. $\displaystyle f_{(Y)}(y) = \frac{n!}{(k - 1)! (n - k)!} \frac{x^{2k - 1}}{2\, 4^{k - 1}}\left(1 - \frac{x^2}{4}\right)^{n - k}$ for $0 < x < 2$.

Answer to Exercise 13.10. Fix the initial draw: $X = x$. Given that value, each $Y_i \sim\text{Unif}(0, 1)$ is independent of the others, and the probability that $Y_i > x$ is $1 - x$. So for fixed $x$, the number of trials $N$ until the first $Y > x$ has a geometric distribution with success probability $p = 1 - x$, and therefore \[ \operatorname{E}[X] = 1 / (1 - x). \] To find the overall expected value, we integrate over all possible $x \ in [0, 1]$: \[ \operatorname{E}[N] = \operatorname{E}[1/(1 - X)] = \int_0^1 \frac{1}{1 - x}\, dx, \] which diverges. Thus, $\operatorname{E}[N] = \infty$.

E.14 Answers for Chap. 14

Answer to Exercise 14.1.

$f(\theta| y)\propto f(y\mid\theta)\times f(\theta)$, where (given): \[ f(y\mid \theta) = (1 - \theta)^y\theta \quad\text{and}\quad f(\theta) = \frac{\theta^{m - 1}(1 - \theta)^{n - 1}}{B(m, n)}. \] Combining then:
\[ f(\theta| y)\propto \theta^{(m + 1) - 1} (1 - \theta)^{(n + y) - 1}. \] which is a beta distribution with parameters $m + 1$ and $n + y$.
Prior: $\operatorname{E}(\theta) = m / (m + n) = 1.2/(1.2 + 2) = 0.375$. So then, $\operatorname{E}(Y) = (1 - p)/p = 1.667$.
Posterior: $\operatorname{E}(\theta) = (m + 1)/(m + 1 + n + y) = 0.3056$; slightly reduced.

D Using R with distributions

F References

.	\(X = 0\)	\(X = 1\)	\(X = 2\)
\(Y = 0\)	\(1/4\)	\(1/4\)	\(0\)
\(Y = 1\)	\(0\)	\(1/4\)	\(1/4\)

	\(C = 0\)	\(C = 1\)
\(D = 0\)	\(6/36\)	\(6/36\)
\(D = 1\)	\(12/36\)	\(12/36\)

	\(Y_1 = 1\)	\(Y_1 = 2\)
\(Y_2 = 0\)	\(2/6\)	\(0\)
\(Y_2 = 1\)	\(1/6\)	\(3/6\)

.	Die 1: 1	2	3	4	5	6
Die 2: 1	\((1, 1)\)	\((2, 1)\)	\((3, 1)\)	\((4, 1)\)	\((5, 1)\)	\((6, 1)\)
2	\((2, 1)\)	\((2, 2)\)	\((3, 2)\)	\((4, 2)\)	\((5, 2)\)	\((6, 2)\)
3	\((3, 1)\)	\((3, 2)\)	\((3, 3)\)	\((4, 3)\)	\((5, 3)\)	\((6, 3)\)
4	\((4, 1)\)	\((4, 2)\)	\((4, 3)\)	\((4, 4)\)	\((5, 4)\)	\((6, 4)\)
5	\((5, 1)\)	\((5, 2)\)	\((5, 3)\)	\((5, 4)\)	\((5, 5)\)	\((6, 5)\)
6	\((6, 1)\)	\((6, 2)\)	\((6, 3)\)	\((6, 4)\)	\((6, 5)\)	\((6, 6)\)

	\(\text{min} = 1\)	\(\text{min} = 2\)	\(\text{min} = 3\)	\(\text{min} = 4\)	\(\text{min} = 5\)	\(\text{min} = 6\)
\(\text{max} = 1\)	1/36	0/36	0/36	0/36	0/36	0/36
\(\text{max} = 2\)	2/36	1/36	0/36	0/36	0/36	0/36
\(\text{max} = 3\)	2/36	2/36	1/36	0/36	0/36	0/36
\(\text{max} = 4\)	2/36	2/36	2/36	1/36	0/36	0/36
\(\text{max} = 5\)	2/36	2/36	2/36	2/36	1/36	0/36
\(\text{max} = 6\)	2/36	2/36	2/36	2/36	2/36	1/36