13 Order statistcs

On completion of this chapter, you should be able to:

• determine the sampling distributions of a given order statistics.
• explain how to find the distributions of order statistics.
• use order statistics in practical problems.

13.1 Introduction

In many applications, information about the minimum value, or the maximum value, in a sample is useful. For example, knowing the maximum water height in a dam is useful for modelling controlled water releases; the mean water height is of little use here. The minimum and maximum values in a sample are examples of order statistics.

More generally, order statistics refer to the values in a sample arranged in increasing order. For a given random sample \(X_1, X_2, \dots, X_n\), the order statistics are defined and denoted as \[ X_{(1)} \le X_{(2)} \le \cdots \le X_{(n)} \] \(X_{(k)}\) is the \(k\)th order statistic, the \(k\)th smallest value in a sample.

Important order statistics in a sample of size \(n\) include the minimum value \(X_{(1)}\), the maximum value \(X_{(n)}\), and the range \(X_{(n)} - X_{(1)}\).

The median is also an important order statistic: \[ \text{median} = \begin{cases} \displaystyle\frac{X_{(n/2)} + X_{(n/2 + 1)}}{2} & \text{for $n$ even;}\\ X_{([n + 1]/2)} & \text{for $n$ is odd.} \end{cases} \] In some circumstances, the median for \(n\) even uses a slightly formula.

The inter-quartile range (IQR)index{Inter-quartile range} is also an order statistic: \[ \text{IQR} = X_{(3n/4)} - X_{(n/4 )}. \] Unless the sample size \(n\) is a multiple of four, the exact order statistics \(X_{(3n/4)}\) and \(X_{(n/4 )}\) may not be defined, and in these situation different ways exist to approximate these order statistics.

Example 13.1 (Median: $n$ odd) Consider a sample of five die rolls, say \(X_i\): \[ x_1 = 5; \quad x_2 = 3; \quad x_3 = 5; \quad x_4 = 2; \quad x_5 = 6. \] The order statistics are \[ x_{(1)} = 2; \quad x_{(2)} = 3; \quad x_{(3)} = 5; \quad x_{(4)} = 5; \quad x_{(5)} = 6. \] The minimum value is \(X_{(1)} = 2\), and the maximum value is \(X_{(5)} = 6\). The median value is \(X_{(3)} = 5\).

Example 13.2 (Median: $n$ even) Consider a sample of six die rolls, say \(Y_i\): \[ y_1 = 1; \quad y_2 = 4; \quad y_3 = 6; \quad y_4 = 2; \quad y_5 = 5 \quad y_6 = 1. \] The order statistics are \[ y_{(1)} = 1; \quad y_{(2)} = 1; \quad y_{(3)} = 2; \quad y_{(4)} = 4; \quad y_{(5)} = 5; \quad y_{(6)} = 6. \] The minimum value is \(y_{(1)} = 1\), and the maximum value is \(y_{(4)} = 6\). The median value is \(\left(X_{(3)} + X_{(4)}\right)/2 = (2 + 4)/2 = 3\), which is not one of the observations in the sample.

As with any statistic, the order statistics have a sampling distribution. The easiest order statistics for which to find the distribution are the maximum value (the \(n\)th order statistic; Sect. 13.2) and the minimum value (first order statistic; Sect. 13.3).

13.2 Sampling distribution of the maximum value

Consider a sample of size \(n\), say \(X_1, X_2, \dots, X_n\), with all \(X_i\) drawn independently from a distribution with density function \(f_X(x)\) and distribution function \(F_X(x)\). Then define \(X_{(n)} = \operatorname{max}\{X_1, X_2, \dots, X_n\}\) as the maximum value in the sample.

The distribution function for \(X_{(n)}\) is \(F_{X_{(n)}}(x) = \Pr(X_{{(n)}} \le x)\), by definition: the probability that the maximum value is less than some given value \(x\). If the value of \(X_{(n)}\) is less than or equal to some value \(x\), then the values in the sample must be less than that value \(x\). Since the observations \(X_1, X_2, \dots X_n\) are all independent and identically distributed, the probability that all observations are less than or equal to some value \(x\) is \[ F_{X_{(n)}}(x) = [F_X(x)]^{n} \] for \(x \in R_X\).

The density function then is found by differentiating \(F_{X_{(n)}}(x)\) with respect to \(x\) (Sect. 3.4), to obtain \[ f_{X_{(n)}}(x) = n [F_X(x)]^{n - 1} \times f_X(x) \] for \(x \in R_X\).

Definition 13.1 (Distribution of the maximum value) Consider a sample of size \(n\), say \(X_1, X_2, \dots, X_n\), with all \(X_i\) drawn independently from a continuous distribution with density function \(f_X(x)\) and distribution function \(F_X(x)\). Then the distribution function for the maximum value (order statistic \(X_{(n)}\)) is \[ F_{X_{(n)}}(x) = \begin{cases} 0 & \text{for $x \le 0$}\\ [F_X(x)]^{n} & \text{for $0 < x < 1$}\\ 1 & \text{for $x \ge 1$.} \end{cases} \] and the density function is \[ f_{X_{(n)}}(x) = n [F_X(x)]^{n - 1} \times f_X(x) \] for \(x\in R_X\).

Example 13.3 (Uniform distribution: maximum value) For the continuous uniform distribution (Sect. 8.2) defined on \([0, 1]\), the density function is \[\begin{equation} f_X(x; 0, 1) = 1 \quad\text{for $0\le x\le 1$}, \tag{13.1} \end{equation}\] and the distribution function is \[ F_X(x; 0, 1) = \begin{cases} 0 & \text{for $x < 0$};\\ \displaystyle x & \text{for $0 \le x \le 1$};\\ 1 & \text{for $x > 1$}. \end{cases} \] Hence, the density function for the maximum value in a sample of size \(n\) is, from Def. 13.1, \[ f_{X_{(n)}}(x) = n\, x^{n - 1} \times 1 = n \, x^{n - 1}, \] for \(0 < x < 1\). In addition, the distribution function is, from Def. 13.1, \[ F_{X_{(n)}}(x) = \begin{cases} 0 & \text{for $x < 0$}\\ x^n & \text{for $0 \le x \le 1$}\\ 1 & \text{for $x > 1$.} \end{cases} \]

Using the density function of the maximum value as given above, the expected value and the variance of the maximum value can be found from their definitions; for example, \[\begin{align*} \operatorname{E}[X_{(n)}] &= \int_0^1 x \cdot n x^{n - 1}\, dx = \frac{n}{n + 1};\\ \operatorname{E}[X^2_{(n)}] &= \int_0^1 x^2 \cdot n x^{n - 1}\, dx = \frac{n}{n + 2};\\ \operatorname{var}[X_{(n)}] &= \frac{n}{n + 2} - \left( \frac{n}{n + 1} \right)^2. \end{align*}\]

For the case where \(n = 10\), then: \[ f_{X_{(n)}}(x) = 10 \, x^{9}, \] for \(0 < x < 1\). In addition, the distribution function is, from Def. 13.1, \[ F_{X_{(n)}}(x) = \begin{cases} 0 & \text{for $x < 0$}\\ x^{10} & \text{for $0 \le x \le 1$}\\ 1 & \text{for $x > 1$.} \end{cases} \] Fig. 13.1 shows the probability density function (left panel) and the distribution function (right panel). For example, the probability that the largest value in a sample of size \(10\) is smaller than \(0.8\) is \[ F_{(10)}(0.8) = 0.8^{10} = 0.1073742\dots \]

The expected value and variance of the maximum value are: \[\begin{align*} \operatorname{E}[X_{(n)}] &= \frac{10}{11} \approx 0.90909;\\ \operatorname{var}[X_{(n)}] &= \frac{10}{12} - \left( \frac{10}{11} \right)^2\approx 0.006887. \end{align*}\] These results can be confirmed using a quick computer simulation:

num_Sims <- 5000
sample_Size <- 10

x_Max <- array( dim = num_Sims)
for (i in 1:num_Sims){
  x <- runif(sample_Size,
             min = 0,
             max = 1)
  x_Max[i] <- max(x) 
}
cat("Mean of the maximum value", mean(x_Max), "\n")
#> Mean of the maximum value 0.908552
cat("Variance of the maximum value", var(x_Max), "\n")
#> Variance of the maximum value 0.006912192

FIGURE 13.1: The distribution of the maximum value for the uniform distribution on \([0, 1]\) in a sample of size \(10\). Left: the probability density function of the maximum value \(X_{(10)}\). Right: the distribution function of the maximum value \(X_{(10)}\). The grey, dotted lines show \(F_{(10)}(0.8)\).

13.3 Sampling distribution of the minimum value

Consider again a sample of size \(n\), say \(X_1, X_2, \dots, X_n\), with all \(X_i\) drawn independently from a distribution with density function \(f_X(x)\) and distribution function \(F_X(x)\). Then define \(X_{(1)} = \operatorname{min}\{X_1, X_2, \dots, X_n\}\) as the minimum value in the sample.

The distribution function for \(X_{(1)}\) is \(F_{X_{(1)}}(x) = \Pr(X_{{(1)}} \le x)\). If the value of \(X_{(1)}\) is less than or equal to some value \(x\), then there must be at least one value less than that value \(x\). Alternatively, this means that we cannot have all the sample values larger than the value \(x\) (as then there must be none that are less than \(x\)).

The probability that all values are larger than \(x\) is \([1 - F_X(x)]^n\) (since all \(n\) values have identical, independent distributions). Hence, the probability that all values are not larger than \(x\) is \[ 1 - [1 - F_X(x)]^n \] for \(x \in R_X\). The density function is found by differentiating \(F_{X_{(1)}}(x)\) with respect to \(x\) (Sect. 3.4), to obtain \[ f_{X_{(1)}}(x) = n [1 - F_X(x)]^{n-1} f_X(x) \] for \(x \in R_X\).

Definition 13.2 (Distribution of the minimum value) Consider a sample of size \(n\), say \(X_1, X_2, \dots, X_n\), with all \(X_i\) drawn independently from a continuous distribution with density function \(f_X(x)\) and distribution function \(F_X(x)\). Then the distribution function for the minimum value (order statistic \(X_{(1)}\)) is \[ F_{(X_1)}(x) = 1 - [1 - F_X(x)]^{n} \] and the density function is \[ f_{(X_1)}(x) = n [1 - F_X(x)]^{n - 1} \times f_X(x) \] for \(x\in R_X\).

Example 13.4 (Uniform distribution: minimum value) For the continuous uniform distribution (Sect. 8.2) defined on \([0, 1]\), the density function and distribution function are giuven in Example 13.3. Using these, the density function for the minimum value in a sample of size \(n\) is \[ f_{X_{(1)}}(x) = n(1 - x)^{n - 1} \times 1 = n (1- x)^{n - 1}, \] for \(0 < x < 1\). In addition, the distribution function is \[ F_{X_{(1)}}(x) = \begin{cases} 0 & \text{for $x < 0$}\\ 1 - (1 - x)^n & \text{for $0 \le x \le 1$}\\ 1 & \text{for $x > 1$.} \end{cases} \]

For the case where \(n = 10\), \[ f_{X_{(1)}}(x) = 10 (1- x)^9, \] for \(0 < x < 1\), and the distribution function is \[ F_{X_{(1)}}(x) = \begin{cases} 0 & \text{for $x < 0$}\\ 1 - (1 - x)^{10} & \text{for $0 \le x\le 1$}\\ 1 & \text{for $x > 0$.} \end{cases} \] Figure 13.2 shows the probability density function (left panel) and the distribution function (right panel). For example, the probability that the smallest value in a sample of size \(10\) is smaller than \(0.2\) is \[ F_{(1)}(0.2) = 1 - (1 - 0.2)^{10} = 0.8926\dots \] This can be confirmed using a small simulation:

num_Sims <- 5000
sample_Size <- 10

x_Min <- array( dim = num_Sims)
for (i in 1:num_Sims){
  x <- runif(sample_Size,
             min = 0,
             max = 1)
  x_Min[i] <- max(x) 
}

cat("Proportion of smallest values less than 0.2: ", 
    round(sum(x_Min) / num_Sims, 3), "\n")
#> Proportion of smallest values less than 0.2:  0.911

Using the density function of the minimum value, the expected value and the variance of the minimum value can be found too; for example, \[ \operatorname{E}[X_{(10)}] = \int_0^1 x \cdot 10(1 - x)^9\, dx = 1/11 = 0.0909\dots \]

FIGURE 13.2: The distribution of the minimum value for the uniform distribution on \([0, 1]\) in a sample of size \(10\). Left: the probability density function of the minimum value \(X_{(1)}\). Right: the distribution function of the minimum value \(X_{(1)}\). The grey, dotted lines show \(F_{X_{(1)}}(0.2)\).

13.4 Sampling distribution of the \(k\)th order statistic

The ideas developed above for the distribution of the minimum and maximum value in a sample can be applied to other order statistics also. Consider a sample from a continuous distribution with density function \(f_X(x)\) and distribution function \(F_X(x)\). The \(k\)th order statistic \(X_{(k)}\) has the distribution function \(F_{X_(k)}(x) = \Pr(X_{(k)}\le x)\). By definition, this is the probability that the \(k\)th smallest value in the sample is less than (or equal to) some value \(x\).

Writing \(X_{(k)} \le x\) means that at least \(k\) of the \(n\) observations are smaller than the value \(x\); that is, \(k, k + 1, \dots n\) of the \(n\) observations are smaller than \(x\).

First, consider the case where exactly \(k\) observations are smaller than \(x\). This means there must be \(k\) observations with a value less than or equal to \(x\); the probability of this is \[ [F_X(x)]^k \] In addition, the remaining \(n - k\) observations must have a value larger than \(x\); the probability of this is \[ [1 - F_{X}(x)]^{n -k} \] The \(k\) observations that are smaller than \(x\) could be located in many different places among the \(n\) values; these \(k\) observations could be in \(\binom{n}{k}\) different arrangements among the sample of size \(n\).

Combining, the probability that exactly \(k\) observations are smaller than \(x\) is \[ \binom{n}{k} \cdot [F_X(x)]^k \cdot [1 - F_{X}(x)]^{n - k}. \]

However, as noted above, there may be more than \(k\) observations smaller than \(x\) also. Following the above ideas, the probability that exactly \(k + 1\) observations are smaller than \(x\) is \[ \binom{n}{k + 1} \cdot [F_X(x)]^{k+1} \cdot [1 - F_{X}(x)]^{n - (k+1)} \] and so on, up to all \(n\) observations being less than \(x\). Summing these probabilities gives \[ \Pr(X_{(k)} \le x) = \sum_{i = k}^n \binom{n}{i} \cdot [F_X(x)]^i \cdot [1 - F_{X}(x)]^{n - i}. \]

From this distribution function, the probability density function can be obtained as \[ f_{X_{(k)}}(x) = \frac{d}{dx} F_{X_{(k)}}(x) = \frac{n!}{(k - 1)!\,(n - r)!}f_{X}(x) [F_{X}(x)]^{k - 1} [1 - F_{X}(x)]^{n - r}, \] for \(n > k \ge 1\) and \(n\) and \(k\) are integers.

Definition 13.3 (Distribution of an order statistic: continuous rv) Consider a sample of size \(n\), say \(X_1, X_2, \dots, X_n\), with all \(X_i\) drawn independently from a continuous distribution with density function \(f_X(x)\) and distribution function \(F_X(x)\). Then the distribution function for the \(k\)th order statistic \(X_{(k)}\) is \[\begin{equation} F_{X_{(k)}}(x) = \Pr(X_{(k)}\le x) = \sum_{i = k}^n \binom{n}{k}\times [F_{X}(x)]^i \times [1 - F_{X}(x)]^{n - i} \tag{13.2} \end{equation}\] and the density function of the \(k\)th order statistic \(X_{(k)}\) is: \[\begin{equation} f_{X_{(k)}}(x) = \frac{n!}{(k - 1)! (n - k)!} [F_X(x)]^{k-1} [1 - F_X(x)]^{n-k} f(x), \tag{13.3} \end{equation}\] where \(n > k > 0\) and \(n\) and \(k\) are integers.

Example 13.5 (Uniform distribution: other order statistics) Consider the second and sixth order statistics from sample of size \(n = 10\) from a Unif\((0, 1)\) distribution (where \(f_X(x)\) and \(F_X(x)\) are given in Example 13.3); using Equation (13.3): \[\begin{align*} f_{X_{(2)}}(x) &= \frac{10!}{1!\, 8!} x (1 - x)^8 = 90 x (1 - x)^8\quad\text{and}\\ f_{X_{(6)}}(x) &= \frac{10!}{5!\, 4!} x^5 (1 - x)^4 = 1260 x^5 (1 - x)^4. \end{align*}\]

Consider simulating \(5\,000\) samples of size \(n = 10\) from a Unif\((0, 1)\) distribution:

n <- 10   # Take samples of size 10

samples2 <- replicate(5000,               # 1000 repetitions
                      sort(runif(n))[2])  # 2nd order statistic
samples6 <- replicate(5000,               # 1000 repetitions
                      sort(runif(n))[6])  # 6th order statistic

The distribution of \(X_{(2)}\) (i.e., samples2) and \(X_{(6)}\) (i.e., samples6) are shown in Fig.  13.3.

FIGURE 13.3: Simulating the distribution of two order statistics for the uniform distribution on \([0, 1]\) with a sample of size \(10\). Left: the distribution of \(X_{(2)}\). Right: the distribution of \(X_{(6)}\). The solid lines show the theoretical distributions.

Example 13.6 (Air conditioner servicing) A new server room has four air-conditioning units installed. The lifetime of each unit (in hours) follows an exponential distribution with mean \(\lambda = 2000\,\text{h}\). The units operate independently. A service technician is called when two of the units fail. We seek the distribution of the time until the call to the technician is made.

Let \(T_1, T_2, T_3, T_4\) denote the lifetimes of the four units. Then: \[ T_i \sim \text{Exponential}(\lambda)\quad\text{for $i = 1, 2, 3, 4$}, \] where \(\lambda = 1/2000\), and the \(T_i\) are independent. That is, \[ f_{T_i}(t)= \frac{1}{\lambda}\exp(-t/\lambda) \quad\text{and}\quad F_{T_i}(t)= \exp(-t/\lambda) \] for \(0 < x < \infty\).

Define the order statistics as \(T_{(1)} < T_{(2)} < T_{(3)} < T_{(4)}\). The technician is called at time \(T_{(2)}\), the second failure. Since we have \(n = 4\) and \(k = 2\), the distribution of \(T_{(2)}\) is (from REF) \[ f_{T_{(2)}}(t) = 6 [\exp(-t/\lambda)]^1 [1 - \exp(-t/\lambda)] ^2 \times \frac{1}{\lambda}\exp(-t/\lambda), \] which is very complicated.

However, the exponential distribution has the memoryless property (REF), so a different approach is much simpler. The time to the first failure \(T_{(1)}\) has the probability density function \[ T_{(1)} \sim \text{Exponential}(4\lambda) \] since any of the \(4\) units can fail first. The time between the first and second failure also has an exponential distribution, due to the memoryless property, this means that \[ T_{(2)} - T_{(1)} \sim \text{Exponential}(3\lambda) \] because only \(3\) units remain after the first failure.

Thus, the total time until the second failure is: \[ T_{(2)} = E_1 + E_2 \] where \[ E_1 \sim \text{Exp}(4\lambda) \quad\text{and}\quad E_2 \sim \text{Exp}(3\lambda). \]

This distribution is not exponential, but the sum of two independent exponentials with different rates.

The expected value is \[ \operatorname{E}[T_{(2)}] = \frac{1}{4\lambda} + \frac{1}{3\lambda} = \frac{1}{\lambda} \left( \frac{1}{4} + \frac{1}{3} \right) = 2000 \cdot \frac{7}{12} = 1166.6\dots\,\text{h}. \]

On average, a technician will be called after about \(1166.67\,\text{h}\).

The PDF of \(T_{(2)}\) can be found using convolution: \[ f_{T_{(2)}}(t) = \int_0^t f_{E_1}(x) f_{E_2}(t - x)\, dx \] where \(f_{E_1}(x) = 4\lambda e^{-4\lambda x}\), and \(f_{E_2}(x) = 3\lambda e^{-3\lambda x}\). This approach can be extended to any \(k\)th failure out of \(n\) components.

13.5 Order statistics for discrete random variables

Working with order statistics is easier with continuous random variables than for discrete random variables, because ties are not possible for continuous random variables (since \(\Pr(X = x) = 0\) for some value \(x\) when \(X\) is a continuous random variable). As a result, the formulas for discrete random variables are more complicated than for continuous random variables, since they need to accommodate the possibility of ties in the sample.

Let \(X_1, X_2, \dots, X_n\) be i.i.d. from a discrete distribution with probability mass function \[ p_X(x) = \Pr(X = x), \] and distribution function \[ F_X(x) = \Pr(X \le x). \] In the discrete case, defining \[ F_X(x^-) = \lim_{t \uparrow x} F_X(t) = \Pr(X < x). \] proves helpful in what follows (see Fig. 13.4). For discrete random variables defined over consecutive integers, \(x^- = x - 1\).

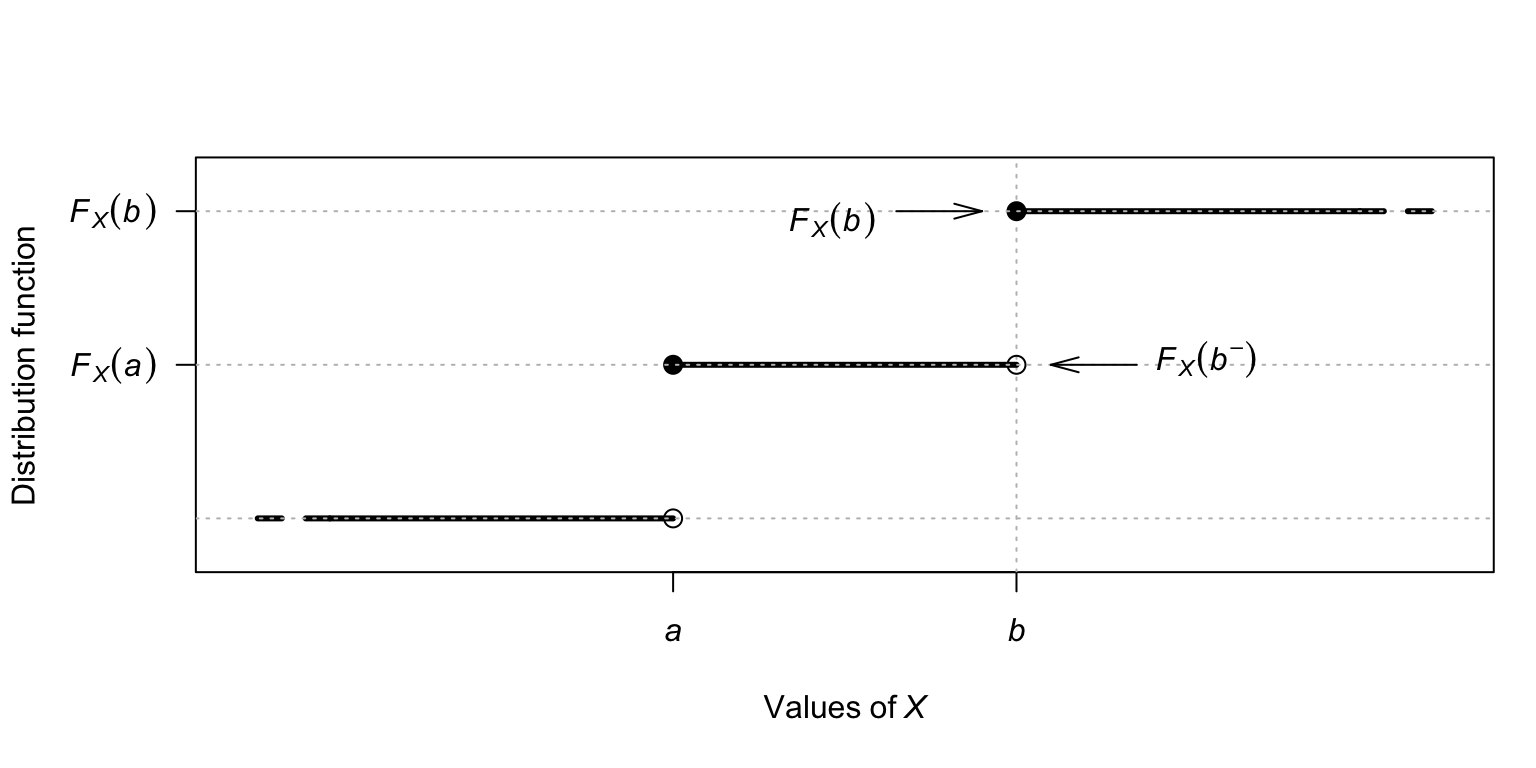
FIGURE 13.4: Explaining the meaning of \(F_X(b^-)\).

We begin with the first order statistic (the minimum value) to establish the general ideas of working with discrete random variables. The first order statistic is \(X_{(1)} = \min\{ X_1, X_2, \dots, X_n \}\); then, following similar logic to the continuous case, \[\begin{align*} F_{X_{(1)}}(x) &= \Pr(X_{(1)} \le x) \\ &= 1 - \Pr(X_{(1)} > x) \\ &= 1 - \Pr(X_1 > x, X_2 > x, \dots, X_n > x) \\ &= 1 - \big[ 1 - F_X(x) \big]^n. \end{align*}\] The probability mass function is the probability that all observations are at least \(x\), but not all are greater than \(x\): \[\begin{align*} p_{X_{(1)}}(x) &= \Pr(X_{(1)} \ge x) - \Pr(X_{(1)} \ge x+1) \\ &= \big[ 1 - F_X(x^-) \big]^n - \big[ 1 - F_X(x) \big]^n. \end{align*}\]

Example 13.7 (Rolling a fair die: minimum) Suppose a fair die is rolled \(n = 10\) times, and the number \(X\) that appears on each roll is recorded. Then \(X \sim\text{Unif}(1, 6)\) and so \[ p_X(x) = \begin{cases} 1/6 & \text{for $x = 1, 2, \dots 6$}\\ 0 & \text{elsewhere} \end{cases} \qquad \text{and} \qquad F_X(x) = \begin{cases} 0 & \text{for $x < 1$}\\ \lfloor x \rfloor/6 & \text{for $1 \le x \le 6$}\\ 1 & \text{for $x > 6$.} \end{cases} \]

Then the distribution function for the minimum value (i.e., \(X_{(1)}\)) is \[\begin{align*} \Pr\big(X_{(1)} \le x\big) &= \big[1 - F_X(x - 1)\big]^{10} \\ &= \begin{cases} 0 & \text{for $x < 1$}\\ \displaystyle 1 - \left[1 -\frac{\lfloor{x}\rfloor}{6}\right]^{10} & \text{for $1 \le x\le 6$}\\ 1 & \text{for $x > 6$} \end{cases} \end{align*}\] for \(1 \le x\le 6\). If we focus on the distribution function at integer outcomes only, \[ F_{X_{(1)}}(x) = 1 - \left(\frac{6 - x}{6}\right)^{10} \qquad\text{at $x = 1, 2\dots, 6$}. \] Since, for dice, the outcomes from rolling are consecutive integers, \(x^- = x - 1\); hence, the corresponding probability mass function is: \[ \Pr\left(X_{(1)} = s\right) = \left(\frac{6 - x}{6}\right)^{10} - \left(\frac{5 - x}{6}\right)^{10} \quad \text{for $x = 1, \dots, 6$.} \] These can be computed in R, then plotted (the dots in Fig. 13.5, left panel):

### THEORETICAL
x <- 1:6
CDF <- c(0,
         1 - ((6 - x)/6)^10)
round(CDF, 4)
#> [1] 0.0000 0.8385 0.9827 0.9990 1.0000 1.0000
#> [7] 1.0000

PMF <- diff(CDF)
round(PMF, 4)
#> [1] 0.8385 0.1442 0.0164 0.0010 0.0000 0.0000

The situation can be simulated and plotted also (the bars in Fig. 13.5, left panel):

### SIMULATION
set.seed(62004) # For reproducibility

# Replicate many sets of 10 rolls of a die
rolls_In_Set <- 10  # Sets f 10 rolls
num_Sims <- 1000    # Number of simulations

rolls <- sample( x = 1:6,
                 size = rolls_In_Set * num_Sims,
                 replace = TRUE)
                 
# Arrange each set of 10 as a row 
rolls <- matrix(data = rolls,
                nrow = num_Sims)

# Find the minimum in each row (i.e., each set of 10 rolls)
min_Roll <- apply(rolls,
                  MARGIN = 1,
                  FUN = "min")
min_Roll <- factor(min_Roll, 
                   levels = c(1:6))

For example, this means that in a set of \(10\) rolls, the probability that the minimum roll is a two is about \[ \Pr( X_{(7)} = 2) \approx 0.14 = 14\%. \]

More generally, for the \(k\)th order statistic \(X_{(k)}\) for a discrete random variable \(X\), let \(X_1, X_2, \dots, X_n\) be i.i.d. from a discrete distribution with \[\begin{align*} p_X(x) &= \Pr(X = x);\\ F_X(x) &= \Pr(X \le x); \text{and}\\ F_X(x^-) &=\Pr(X < x). \end{align*}\]

First, define the number of observations less than or equal to \(x\) as \[ Y = \sum_{j = 1}^n I\{X_j\le x\} \sim \mathrm{Binom}\!\left(n,\,F_X(x)\right). \] Then \[\begin{align*} F_{X_{(k)}}(x) &= \Pr\bigl(X_{(k)} \le x\bigr) = \Pr(Y \ge k) \\ &= \sum_{i = k}^n \binom{n}{i}\,F_X(x)^{i}\,[1 - F_X(x)]^{\,n - i}. \end{align*}\]

For a discrete random variable \(X\), the probability mass function is how much the distributions function ‘jumps’ at the values of \(x\). So, the probability mass function for \(X_{(k)}\) can be found from the distribution function as \[\begin{align*} p_{X_{(k)}}(x) &= \Pr\bigl(X_{(k)}=x\bigr)\\ &= F_{X_{(k)}}(x) - F_{X_{(k)}}(x^-) \notag\\ &= \sum_{i=k}^n \binom{n}{i}\,[F_X(x)]^{i}\,[1-F_X(x)]^{\,n-i} \;- \notag\\ &\qquad \qquad \sum_{i = k}^n \binom{n}{i}\,[F_X(x^-)]^{i}\,[1 - F_X(x^-)]^{\,n - i}. \end{align*}\]

Definition 13.4 (Distribution of an order statistic: discrete rv) Consider a sample of size \(n\), say \(X_1, X_2, \dots, X_n\), with all \(X_i\) drawn independently from a discrete distribution with probability mass function \(f_X(x)\) and distribution function \(F_X(x)\). Then the distribution function of the \(k\)th order statistic \(X_{(k)}\) is \[\begin{equation} F_{X_{(k)}}(x) = \Pr\big(X_{(k)} \le x\big) = \sum_{i = k}^n \binom{n}{i}\, F_X(x)^{i}\,[1 - F_X(x)]^{n - i} \tag{13.4} \end{equation}\] The probability mass function of the \(k\)th order statistic \(X_{(k)}\) at integer values of \(x\in R\) is: \[\begin{align} p_{X_{(k)}}(x) &= F_{X_{(k)}}(x) - F_{X_{(k)}}(x^-)\notag \\ &= \sum_{i = k}^n \binom{n}{i} \left\{ F_X(x)^{i}\,[1 - F_X(x)]^{\,n - i} - F_X(x^-)^{i}\,[1 - F_X(x^-)]^{\,n - i} \right\} \tag{13.5} \end{align}\] where \(n > k > 0\) and \(n\) and \(k\) are integers.

Example 13.8 (Rolling a fair die: general order statistic) Continuing Example 13.7, where a standard six-sided die is rolled \(10\) times. The general \(k\)-th order statistic \(X_{(k)}\) is \[ F_{X_{(k)}}(x) = \Pr\big(X_{(k)} \le x\big) = \sum_{i = k}^{10} \binom{10}{i}\,\left(\frac{x}{6}\right)^{i}\,\left(1 - \frac{x}{6}\right)^{10 - i}, \] for \(x\in\{1,\dots,6\}\).

Since, for dice, the outcomes from rolling are consecutive integers, \(x^- = x - 1\), the corresponding probability mass function is found using the discrete difference \[\begin{align*} \Pr\big(X_{(k)} = x\big) &= \Pr\big(X_{(k)}\le x\big) - \Pr\big(X_{(k)}\le x - 1\big)\\ &= \sum_{i = k}^{10} \binom{10}{i} \left\{\left(\frac{x}{6}\right)^{i}\,\left(1 - \frac{x}{6}\right)^{10 - i} - \right.\\ &\phantom{={}\sum_{i = k}^{10} \binom{10}{i}\Huge\{} \left.\left(\frac{x - 1}{6}\right)^{i}\,\left(1 - \frac{x - 1}{6}\right)^{10 - i}\right\} \end{align*}\] So, for instance, the seventh order statistic (i.e., where \(k = 7\)) is \[ \Pr\big(X_{(7)} = x\big) = \sum_{i = 7}^{10} \binom{10}{i} \left\{\left(\frac{x}{6}\right)^{i}\,\left(1 - \frac{x}{6}\right)^{10 - i} - \left(\frac{x - 1}{6}\right)^{i}\,\left(1 - \frac{x - 1}{6}\right)^{10 - i}\right\} \] for \(x\in\{ 1, 2, 3, 4, 5, 6\}\). These can be computed in R, then plotted (the dots in Fig. 13.5, right panel):

### SIMULATED 
# Simulation, using  rolls  from the last Example
Order_Stats_7 <- apply( rolls,
                        MARGIN = 1, # i.e., across rows
                        FUN = function(x){ sort(x)[7]} )

Order_Stats_7 <- factor(Order_Stats_7, 
                        levels = c(1:6))
table(Order_Stats_7)/num_Sims
#> Order_Stats_7
#>     1     2     3     4     5     6 
#> 0.000 0.009 0.158 0.378 0.383 0.072

The situation can be simulated and plotted also (the bars in Fig. 13.5, right panel):

### SIMULATED 
# Simulation, using  rolls  from the last Example
Order_Stats_7 <- apply( rolls,
                        MARGIN = 1, # i.e., across rows
                        FUN = function(x){ sort(x)[7]} )

Order_Stats_7 <- factor(Order_Stats_7, 
                        levels = c(1:6))
table(Order_Stats_7)/num_Sims
#> Order_Stats_7
#>     1     2     3     4     5     6 
#> 0.000 0.009 0.158 0.378 0.383 0.072

### THEORETICAL
x_Values <- 1:6
i <- 7:10
DF <- array( dim = 6)

for (x in seq_along(x_Values)){
   DF[x] <- sum( choose(10, i) *
                 (x/6)^i * ( (1 - (x/6)))^(10 - i) )
}

PMF <- diff( c(0, DF) )
round(PMF, 3)
#> [1] 0.000 0.019 0.152 0.387 0.371 0.070

For example, this means that, in a set of \(10\) rolls, the probability that the seventh smallest roll is a two is about \[ \Pr( X_{(7)} = 2) \approx 0.019 = 1.9\%. \]

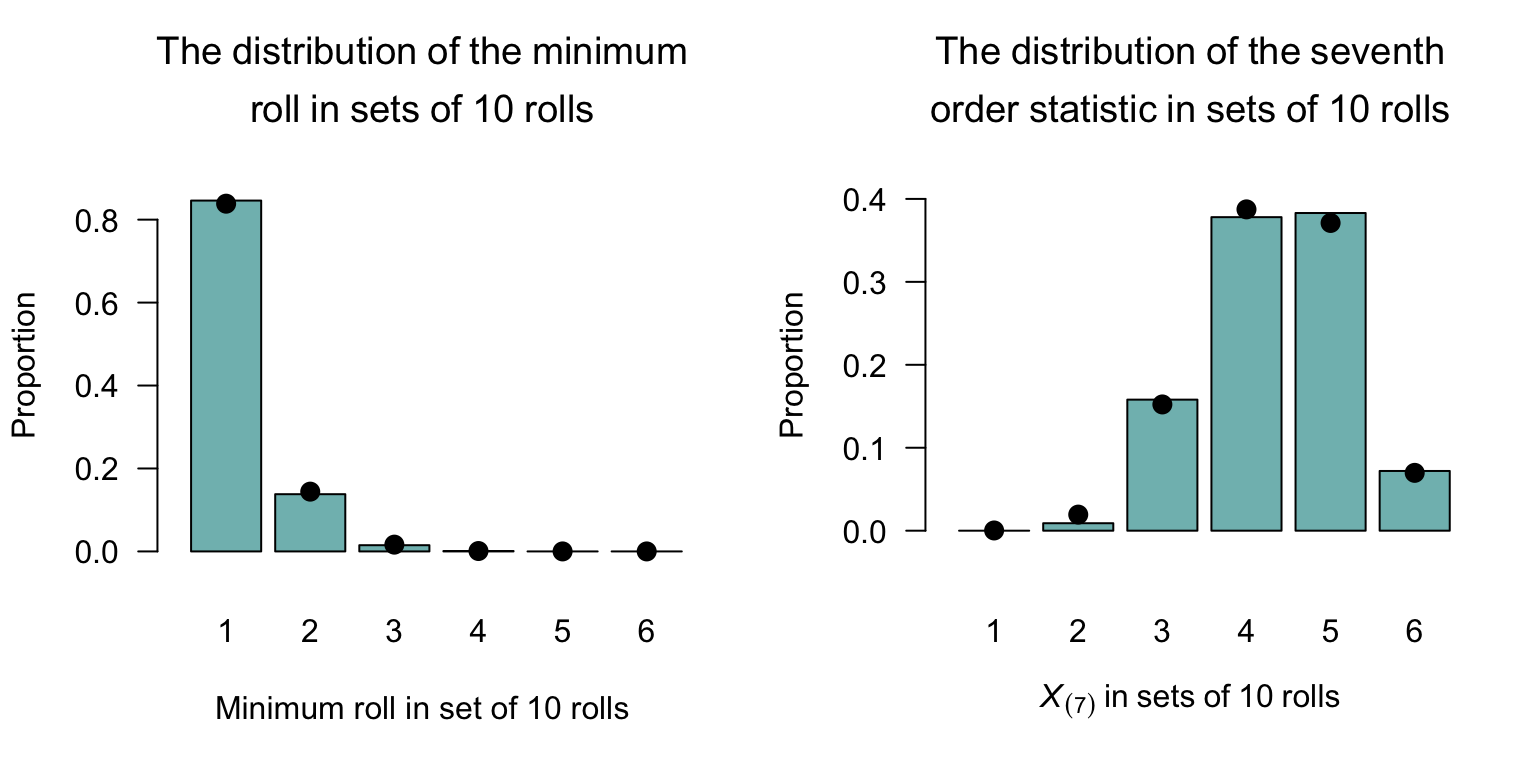
FIGURE 13.5: Left: the distribution of the first order statistic (the minimum roll), in sets of \(10\) rolls. Right: the distribution of the \(7\)th order statistic, in sets of \(10\) rolls. In both cases, the bars show the values from \(1\,000\) simulated sets of \(10\) rolls, and the solid dots are the theoretical values.

13.6 Quantiles and order statistics

So far, order statistics have been defined. A similar, but different, concept is that of quantiles

For a random variable \(X\) with distribution function \(F_X(x)\), the \(p\)-th quantile \(q_p\) is \[ q_p = F^{-1}(p) = \inf \{x \in \mathbb{R} : F(x) \ge p \} \quad \text{for $0 < p < 1$}. \] Quantiles are fixed values determined by the distribution, whereas order statistics are random variables derived from a finite sample. Sample quantiles are typically estimated from the data using order statistics.
For example, the sample median is \(X_{(\lceil n/2 \rceil)}\) (or an average of two adjacent order statistics when \(n\) is even).

General order statistics in R are found by first sorting the sample values using sort(), and the selecting the relevant values from the result using indexing; for example, sort(x-Values)[3] selects the third sorted value from the sample.

R can also find quantiles, using the quantile() function. quantile(x, probs) computes the order statistics specified as probabilities (called quantiles) defined in prob. Generally, the exact quantiles cannot be found, and are approximated. R offers nine different methods for approximating quantiles that cannot be exactly defined (Hyndman and Fan 1996).

Example 13.9 (Quantiles in R)

set.seed(9901) # For reproducibility

x_Sample <- runif(50, 
                  min = 0, 
                  max = 1)
# Place sample observations in order
x_Sort <- sort(x_Sample)

# Examine first few values:
head( round( x_Sort, 4) )
#> [1] 0.0041 0.0309 0.0310 0.0324 0.0411 0.0430

# Compute 25th quantiles (first quartile)
# Using each of the none different methods in R:
for (method in (1:9)){
  cat("Method ", method, ": ",
      round( quantile(x_Sort, 0.25, type = method), 5),
      "\n",
      sep = "")
}
#> Method 1: 0.17359
#> Method 2: 0.17359
#> Method 3: 0.17055
#> Method 4: 0.17207
#> Method 5: 0.17359
#> Method 6: 0.17283
#> Method 7: 0.17715
#> Method 8: 0.17334
#> Method 9: 0.1734

13.7 Exercises

Selected answers appear in Sect. E.13.

Exercise 13.1 Prove that the probably density function for the order statistics in the case of the continuous uniform distribution, shown in Eq. (13.1), is a valid density function. (Hint: observe the similarity between Eq. (13.1) and the beta density function in Sect. 8.6.)

Exercise 13.2 Prove that the expected value and variance of the order statistics in the case of the continuous uniform distribution are \[ \operatorname{E}[X] = k/(n + 1)\qquad\text{and}\qquad \operatorname{var}[X] = \frac{k (k + 1)}{(n + 1)(n + 2)}, \] as in Sect. 13.4. (Hint: observe the similarity between Eq. (13.1) and the beta density function in Sect. 8.6.)

Exercise 13.3 Find the distribution of the order statistics for a sample of size \(n\) drawn from the continuous uniform distribution defined on \([-1, 1]\).

PLOTS??

Exercise 13.4 Find the distribution of the order statistics for samples of size \(n\) drawn from the continuous distribution \[ f_Y(y) = y/2\quad\text{for $0 < y < 2$} \] and zero elsewhere.

PLOTS

Exercise 13.5 Suppose a sample of \(n\) independent values is taken from the exponential distribution \(\text{Exp}(\lambda)\) (REF).

1. Determine the distribution function for the minimum value, \(X_{(1)}\).
2. Hence determine the density function for the minimum value, \(X_{(1)}\).
3. What is the probability that the minimum value in a sample of size \(n\) is larger than \(\lambda/2\)?
4. Compute the expected value of the minimum value in the sample.

PLOTS

Exercise 13.6 Suppose a sample of \(n\) independent values is taken from the exponential distribution \(\text{Exp}(\lambda)\) (REF).

1. Determine the distribution function for the maximum value, \(X_{(n)}\).
2. Hence determine the density function for the maximum value, \(X_{(n)}\).
3. What is the probability that the maximum value in a sample of size \(n\) is larger than \(\lambda/2\)?
4. Compute the expected value of the maximum value in the sample.

PLOTS

Exercise 13.7 A new computer server room has four air-conditioning units installed. The lifetime of each unit follows an exponential, with a mean lifetime of \(2000\,\text{h}\). When two units fail, a service technician is called.

1. Describe the distribution showing the wait time until a technician need to be called.

Exercise 13.8 Consider Equation (13.5), which gives the \(k\)th order statistic for a discrete random variable.

1. Show that the expression given for the probability mass function for the minimum value is given by using \(k = 1\) in Equation (13.5).
2. Use Equation (13.5) to find a formula for the probability mass function for the maximum value.

Exercise 13.9 The probability mass function for the \(k\)th order statistic can be found in a different way than shown in Sect. 13.5. First, define \[\begin{align*} a &= F_X(x^-) = \Pr(X < x);\\ b & = p_X(x) = \Pr(X = x); \text{and}\\ c &= 1 - a - b = \Pr(X > x), \end{align*}\] and use \((R, S, T)\) to denote the number of observations that are less than, equal to, and greater than \(x\), respectively.

1. Show that \((R,S,T) \sim \mathrm{Multinomial}\big(n; a,b,c\big)\).
2. Consider the discrete random variable \(X\), where \[ p_X(x) = \begin{cases} 0.2 & \text{for $x = 1$};\\ 0.5 & \text{for $x = 2$};\\ 0.3 & \text{for $x = 3$};\\ 0 & \text{elsewhere.} \end{cases} \] Show that the above expressions and Equation (13.4) are equivalent for the case \(n = 3\) and finding the second order statistic \(X_{(2)}\).

Exercise 13.10 Suppose you choose a number at random from the continuous uniform distribution between \(0\) and \(1\). Then, you keep choosing numbers from this \(\text{Unif}(0, 1)\) distribution until you obtain a number larger than the one you started with. You record the number of times you have to select a number before you have success (i.e., a larger number that teh initially-selected number).

More precisely:

1. Let \(X\sim\text{Unif}(0, 1)\), your initial number.
2. You then draw \(Y_1, Y_2, \dots\sim\text{Unif}(0, 1)\), i.i.d., until you get a value \(Y_n > X\).
3. Your score is \(N\), the number of trials until this happens.

What is the expected value of \(N\), the number of values to draw to exceed the initially-selected number?

---

Peter K. Dunn, 2024: CC BY-NC-SA 4.0