1 Essentials of set theory

UpOn completion of this chapter you should be able to:

define sets, and define the elements of sets.
define the cardinality of sets.
perform basic set operations.

1.1 Introduction

Imagine if life was deterministic! The commute to the gym, university or work would always take exactly the same length of time; weather predictions would always be accurate; you would know exactly what lotto numbers would be drawn on the weekend…

However, life is full of unpredictable variation.

Variation may be unpredictable, but patterns still emerge. We may not know what the next toss of a coin will produce… but we see a pattern in the long run: a Head appears about half the time.

Probability is one of the tools used to describe and understand this unpredictability. Distribution theory is about describing the patterns in this unpredictability using probability. Statistics is about data collection and extracting information from data, using probability and distribution theory.

In most fields of study, situations exist where being certain is almost impossible, and so probability is necessary:

What is the chance that a particular share price will crash next month?
What are the odds that a medical patient will suffer from a dangerous side-effect?
How likely is it that a dam will overflow next year?
What is the chance of finding a rare bird species in a given forest?

To answer these questions, a framework is needed: concepts like probability need defining, and notation and theory are required. These tools are important for modelling real-world phenomena, but also for providing a firm mathematical foundation for the theory of statistics.

This chapter covers the concept of probability, introduces notation and definitions, and develops some theory useful in working with probabilities.

1.2 Sets

The basis of probability is working with sets, which we first define.

Definition 1.1 (Sets) A set is a well-defined, unordered collection of distinct elements, usually denoted using a capital letter: $A$.

The use of ‘distinct’ means that no elements is repeated; notice that the order of the elements in the set is not relevant. The phrase ‘well-defined’ means that it must be clear whether any given element is in the set (‘belongs to the set’) or is not in the set (‘does not belong to the set’).

The elements can be interpreted widely, and can refer to letters, digits, names, suits in a packof cards, numbers, words, animals, people, machine components, plants… or even other sets.

Definition 1.2 (Elements) Distinct elements of a set $A$ are usually denoted by lower-case letters, and are shown to belong to a set by enclosing them in braces: \[ A = \{ a_1, a_2, a_3, a_4\}. \]

Example 1.1 (Sets) These two sets are equal, since the order of the elements does not matter: \[\begin{align*} A &= \{\text{Brisbane}, \text{Sydney}, \text{Hobart}, \text{Melbourne}, \text{Adelaide}, \text{Perth}\};\\ B &= \{\text{Hobart}, \text{Melbourne}, \text{Perth, }\text{Brisbane}, \text{Sydney}, \text{Adelaide}\}. \end{align*}\] Both sets contain a collection of six distinct elements (‘Australian state capital cities’). We can write $A = B$.

In contrast, \[ C = \{\text{Brisbane}, \text{Sydney}, \text{Hobart}, \text{Sydney}, \text{Hobart}, \text{Hobart} \} \] is not a set, since the elements are not distinct; ‘Sydney’ and ‘Hobart’ are repeated.

Example 1.2 (Examples of sets) We could define the set $M$ as: \[ M = \{\text{Echidnas}, \text{Platypuses}\}, \] $M$ is the set of all known monotremes. Set $M$ has two elements.

We could define the set $E$ as \[ E = \{1, 3, 5, 7, 9\}, \] the set of all odd digits. Set $E$ has five elements.

Then, we could define the set $W$ as: \[ W = \{ M, E\} = \{ (\text{Echidnas}, \text{Platypuses}), (1, 3, 5, 7, 9)\}. \] The set $W$ contains two elements: the two sets $M$ and $E$.

The symbol ‘$\in$’ is used to denote that an element is a member of a set; the symbol ‘$\notin$’ is used to denote that an element is not a member of a set. If an element $a$ is in the set $A$, we write $a \in A$, and we say ‘$a$ is an element of set $A$’.

Example 1.3 (Elements of sets) For set $A$ in Example 1.1, we could write \[ \text{`Hobart'} \in A \] to indicate that ‘Hobart’ is a member of set $A$. Similarly, we could write \[ \text{`Canberra'} \notin A \] to indicate that ‘Canberra’ is not a member of set $A$.

1.3 Defining the elements of sets

The elements of sets can be defined in various ways:

by enumerating (listing) the individual elements;
by describing what is common to all elements of the set, by using a description or by stating a pattern; or
by using a rule.

Whichever method is used, any given element must be clearly in a set or not in a set.

Example 1.4 (Elements in a set) Set $A$ in Example 1.1 has its elements listed. The elements could also be described by defining set $A$ as ‘the set of capital cities in Australian states’.

‘Canberra’ is not an element of the set, since Canberra is not an Australia state capital.

Example 1.5 (Defining elements of a set) Define the set $L$ as the ‘set of books at the local library with more than two authors’. Listing the elements of the set is difficult, but the definition clearly allows us to distinguish between a book that is in the set and a book that is not in the set.

The elements of the set are described using a rule.

1.4 Specific sets

Some specific sets are useful and often used, and are given names and/or symbols to represent them.

A set with no elements is given a special name: the empty set.

Definition 1.3 (Empty set) The null set, or the empty set, has zero elements, and is denoted by $\varnothing$.

Notice that the set itself is denoted $\varnothing$, and the number of elements is $0$.

In contrast, the universal set is the set of all elements under consideration, for a specific context.

Definition 1.4 (Universal set) The universal set is the set of all elements that could be considered in a specific context. It is often denoted by $S$, $U$ or $\Omega$.

In practice, a universal is almost always defined (or assumed). Theoretically, this is not true, to avoid difficulties like that in *Russell’s paradox’.

Russell’s paradox, discovered by Bertrand Russell in 1901, is a famous set-theory paradox.

Consider the set $R$, whose elements are all sets that are not members of themselves. Is $R$ a member of itself?

Consider the two options:

$R$ is a member of itself (that is, $R \in R$). By the definition of $R$ (the set of all sets not members of themselves), if $R$ is a member of itself, then it satisfies the condition of not being a member of itself. This leads to a contradiction: assuming $R$ is a member of itself leads to the conclusion that $R$ is not a member of itself.
R is not a member of itself (that is, $R \notin R$). If $R$ is not a member of itself, then it meets the criterion for being included in $R$. Therefore, $R$ must be a member of itself. This also leads to a contradiction: assuming $R$ is not a member of itself leads to the conclusion that $R$ is not a member of itself.

Both cases lead to a contradiction. If set $R$ is allowed to exist, it leads a breakdown of set theory. To prevent such a paradox, modern set theory (such as ZFC) places restriction on how sets can be formed (though we will not discuss these limits).

Example 1.6 (Null set) Consider rolling a standard, fair six-sided die, and observing the uppermost face. Only six options are possible, so in this context we could define the universal set as \[ U = \{1, 2, 3, 4, 5, 6\}. \] Then, the set $B$ of rolls greater than $4$ would contain the two elements \[ B = \{5, 6\}. \] Also, the set $C$ of rolls greater than $10$ would contain no elements, and so is the empty set \[ C = \varnothing. \] Notice that we do not write $C = \{\varnothing\}$; the symbol $\varnothing$ itself represents a set (with no elements). If we write \[ D = {\varnothing}, \] then set $D$ has one element, and that element is the empty set.

Some special sets of numbers are useful to define:

Natural (or counting) numbers are denoted $\mathbb{N}$: $\{1, 2, 3, \dots\}$.
Integers are denoted $\mathbb{Z}$: $\{\ldots, -2, 1, 0, 1, 2, 3, \dots\}$.
Rational numbers are denoted $\mathbb{Q}$.
Real numbers are denoted $\mathbb{R}$.
Positive real numbers are denoted $\mathbb{R}_{+}$.
Negative real numbers are denoted $\mathbb{R}_{-}$.
Complex numbers are denoted $\mathbb{C}$.

Some authors include $0$ in the set of natural numbers, and some do not.

1.5 Types of sets and cardinality

Sets can be:

finite (informally: the elements can be counted; the number of elements is finite);
countable infinite (informally: the elements could be counted in principle… but there are an infinite number of them); or
uncountably infinite (informally: the elements in the set cannot be counted).

In sets that are finite or countably infinite, a single element of the set is called an element or a sample point. As above, write $a\in A$ to denote that element $a$ belongs to a set $A$.

Example 1.7 (Defining elements of a set) Define set $A$ as \[ A = \left\{ \text{Countries whose names begin and end with the letter `A'}\right\}. \] The elements of $A$ include, for example, ‘Austria’, ‘Antigua and Barbuda’ and ‘Albania’. $A$ contains a finite number of elements.

1.5.1 Finite sets

If the number of elements in a set can be counted, the set is called a finite set. In other words, a set is finite if it has exactly $n$ distinct elements for some non-negative integer $n$. If $n = 0$ (that is, the set contains no elements), the set is the empty set.

The two sets $A$ and $B$ in Example 1.1 are finite sets, as they contain a finite number of elements ($n = 6$).

Example 1.8 (Defining elements of a finite sets) Define the set $S$ as the ‘set of suits in a standard pack of cards’. Then, $S = \{\clubsuit, \spadesuit, \heartsuit, \diamondsuit\}$. We can write, for example, that $\spadesuit \in S$.

The elements of the set are listed; the set has four elements.

Example 1.9 (Defining elements of a finite sets) Define the set $O$ as the ‘set of odd numbers between $0$ and $100$’. Alternatively, the elements of the set can defined by giving the pattern: \[ O = \{1, 3, 5, 7, 9, \dots 95, 97, 99\} \] Set $O$ has $50$ elements.

Example 1.10 (Finite sets) Define set $B$ as ‘the even numbers after rolling a single die’; then,

B = {⚁, ⚃, ⚅}

The set $B$ is finite, with three elements.

1.5.2 Countably infinite sets

Sets can also be countably infinite. A set is countably infinite if its distinct elements can be counted or listed in principle, but there are an infinite number of such elements.

Definition 1.5 (Countably infinite set) A set is called countably infinite if its elements can be put into a one-to-one correspondence with the natural numbers \[ N = \{1, 2, 3, \dots\}. \] In other words, the elements can be listed or enumerated in an infinite sequence $\{a_1, a_2, a_3, \dots\}$ without missing any elements, with each element appears just once.

Example 1.11 (Countably infinite sets) Define $S$ as the number of rolls of a die needed to roll a ⚅. The number of rolls needed could be $1$ or $2$ or $3$… in theory, no upper limit exists. That is, the set $S$ is \[ S = \{1, 2, 3, 4, \dots\} \] Set $S$ is countably infinite.

Example 1.12 (Countably infinite sets) Define the set $O$ as the ‘set of odd numbers’. The elements of the set can be described (odd numbers’), or by giving the pattern: \[ O = \{1, 3, 5, 7, 9, \dots\} \] Set $O$ is countably infinite.

1.5.3 Uncountably infinite sets

Some sets cannot be described by listing the elements, even by using an infinite sequence. These are called uncountably infinite sets. Uncountably infinite sets cannot be described by listing the elements.

Definition 1.6 (Uncountably infinite sets) A set is called uncountably infinite if the elements of the set cannot be counted (i.e., the set contains an infinite number of elements), and the elements of the set cannot all be listed in a sequence like $a_1$, $a_2$, $a_3$, $\dots$ without missing some elements.

Example 1.13 (Uncountably infinite sets) The set $R$ refers to the positive real numbers, which is an uncountably infinite set. The elements of $R$ cannot be listed without missing some elements. For instance, an infinite number of elements exists between the elements $0$ and $0.0001$.

Set $R$ is uncountably infinite.

Example 1.14 (Uncountably infinite set) Consider the heights of people. Between the two heights $173\,\text{cm}$ and $174\,\text{cm}$, an infinite number of heights exist: $173.1\,\text{cm}$, $173.01\,\text{cm}$, $173.001\,\text{cm}$, $173.0001\,\text{cm}$, and so on.

The set of heights in uncountably infinite.

Since the elements of uncountably infinite sets can be listed—even with a pattern—the elements of uncountably infinite sets are often concisely defined using set-builder notation. (Set-builder notation can be used for any sets, but are especially useful for uncountably infinite sets.)

Set-builder notation usually has the format: \[\begin{align*} A &= \{ x \mid \text{some condition for $x$ to belong to the set}\}, \text{or}\\ A &= \{ x : \text{some condition for $x$ to belong to the set}\}. \end{align*}\] In this notation, $\{\dots\}$ means that $A$ is a set; $x$ is a variable representing the elements of the set $A$; the colon or vertical bar is read as ‘such that’, and is followed by the condition for $x$ to belong to the set $A$. Often, the notation to the left of the ‘such that’ defines the universal set for the context.

Example 1.15 (Set-builder notation) Consider the set defined by \[ F = \{s \in \text{Names of students in a certain course} \mid \text{students whose mark is less than $50\%$}\}. \] This is read as ‘$F$ is the set of all student names in a certain course $s$, such that the elements $s$ are the names of all students in that course with a mark less than $50$%’. That is, $F$ represents the set of all students in that specific course who scored less than $50$%.

Example 1.16 (Set-builder notation) Consider the set defined by \[ B = \{x \in \text{Animal species}: \text{$x$ is an animal species with two legs}\} \] This is read as ‘$B$ is the set of all animals species $x$, such that the elements $x$ are all animal species with two legs’. We could also have written \[ B = \{x : \text{$x$ is an animal species with two legs}\} \]

Example 1.17 (Set-builder notation) Consider the set defined by \[ V = \{x \in \text{letters in the alphabet} \mid \text{$x$ is a vowel}\}. \] This is read as ‘$V$ is the set of all letters $x$, such that the elements $x$ are all vowels’.

Example 1.18 (Set-builder notation) Consider the set defined by \[ P = \{y \in \mathbb{Z} : \text{$y$ is a two-digit integer}\}. \] This is read as ‘$P$ is the set of integers $y$, such that the elements $y$ are all two-digit integers’.

Example 1.19 (Throwing a cricket ball) Consider throwing a cricket ball. Let $D$ be the set of all possible distances (in metres) that the ball could be thrown; then \[ D = \{ d \in \mathbb{R} \mid d \ge 0 \}. \] The cardinality of $D$ is uncountably infinite.

Example 1.20 (Uncountably infinite sets) Define $C$ as the set of ‘all possible distances travelled by cars in Europe over one year’. Set $C$ is uncountably infinite, and can be defined as \[ C = \{c \in \mathbb{R} \mid c \ge 0 \}. \]

1.5.4 Cardinality

Cardinality refers to the number of elements of a set. The cardinality of a finite set is easy to describe in principle: it is the number of elements in the set. The number of elements in a set with finite cardinality is denoted $|A|$.

Example 1.21 (Cardinality of finite sets) The set $S$, defined in Example 1.8, is \[ S = \{\clubsuit, \spadesuit, \heartsuit, \diamondsuit\}. \] The elements of the set are listed; the set has four elements. That is, $|S| = 4$.

Countably infinite sets and uncountably infinite sets both have infinite cardinality.

Countably infinite sets and uncountably infinite sets both have infinite cardinality, but different infinite cardinalities. Informally, we can write that $|A| = \infty$ for both countably infinite sets and uncountably infinite sets.

More formally:

if $A$ is a countably infinite set then $|A| = \aleph_0$, where $\aleph_0$ (‘aleph-null’) is the smallest infinite cardinality.
if $A$ is an uncountably infinite set then $|A| = \mathfrak{c}$ where $\mathfrak{c}$ (the ‘cardinality of the continuum’) is a larger cardinality that $\aleph_0$. Sometimes $|\mathbb{R}|$ is used in place of $\mathfrak{c}$.

Georg Cantor showed that \[ \mathfrak{c} = 2^{\aleph_{0}} > \aleph_0. \]

1.6 Operations on sets

Sets can be combined in various ways, which sometimes makes defining sets easier too. Various operations are defined for sets.

Definition 1.7 (Set operations) Consider two sets $A$ and $B$, and a universal set $S$. The following operations are defined.

Intersection:
The intersection of of sets $A$ and $B$, written as $A\cap B$, is the set of elements in both $A$ and $B$: $A\cap B = \{x \mid x\in A \text{ and } x \in B\}$.
Union:
The union of sets $A$ and $B$, written as $A\cup B$, is the combined set of all the elements in either $A$ or $B$, or in both: $A\cup B = \{x \mid x\in A \text{ or } x \in B\}$.
Complement:
The complement of set $A$, written $A^c$, is all the elements of $S$ that are not in set $A$: $A^c = \{x \mid x\notin A\}$.
Difference, set difference or set subtraction:
The difference between sets $A$ and set $B$, written $A\setminus B$ or $A - B$, is all the elements in $A$ that are not in set $B$: $A\setminus B = \{x \mid x\in A \text{ and } x \notin B\}$.
Cartesian product:
The Cartesian product of $A$ and $B$, written $A\times B$, is the combination of all elements of $A$ with all elements of $B$. For example, if $A = \{ 1, 2\}$ and $B = \{10, 20\}$, then $A\times B = \{(1, 10), (1, 20), (2, 10), (2, 20) \}$.
Subset:
$A$ is a subset of $B$, written $A\subseteq B$, if every elements of $A$ is also an element of $B$. (Set $B$ may also have elements that are not in $A$.) This definition requires that $A$ is equal to or smaller than $B$.
Proper subset:
This definition requires that $B$ has at least one element that is not in $A$.

Two sets whose intersection is the empty set (i.e., if $A\cap B = \varnothing$ for two sets $A$ and $B$) the sets are called disjoint sets.

The visual representation in Fig. 1.1 may help clarify some of these definitions. These diagrams are called Venn diagrams.

Be aware of variations in notation! Other notation for the complement of an event $A$ (everything not in event $A$), which we denote as $A^c$, includes $\overline{A}$ or $A'$.

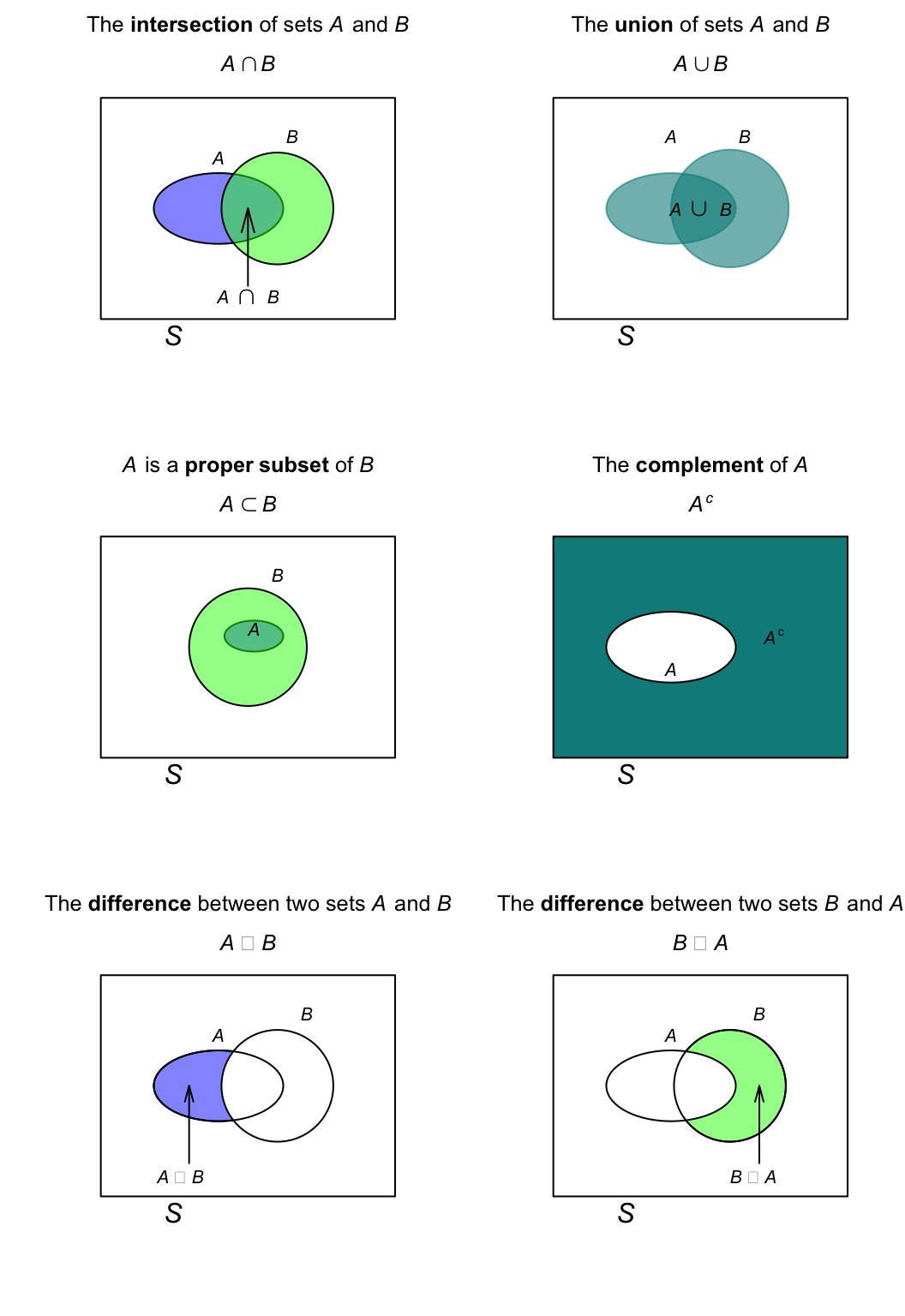
Venn diagrams showing intersection, union, proper subset, complement and set differences. The rectangle represents the universal set, $S$.

FIGURE 1.1: Venn diagrams showing intersection, union, proper subset, complement and set differences. The rectangle represents the universal set, $S$.

Example 1.22 (Relationships between sets) Suppose we define these sets: \[\begin{align*} C &= \{ 0, 1, 2, 3, 4, 5\};\\ D &= \{ 4, 5, 6, 7\};\\ E &= \{ 6 \}. \end{align*}\] Then: \[\begin{align*} C \cap D &= \{ 4, 5\}; & C \cup D &= \{ 0, 1, 2, 3, 4, 5, 6, 7\};\\ E &\in D; & E &\notin C;\\ C \cap E &= \varnothing; & D \cap E &= D;\\ C\setminus D &= \{0, 1, 2, 3\}; & D\setminus C &= \{6, 7\}. \end{align*}\]

Example 1.23 (Relationships between sets) Suppose we define these sets: \[\begin{align*} U &= \{\text{All the digits}\} = \{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9\};\\ B &= \{ 6, 7, 8, 9\};\\ E &= \{ 2, 4, 6, 8\}. \end{align*}\] Here, $U$ is the universal set, the set of all digits, Then, for example: \[\begin{align*} U \cap B &= \{ 6, 7, 8, 9 \} = B; & B \cup E &= \{2, 4, 6, 7, 8, 9\};\\ B &\in U; & U &\notin B;\\ B \cap E &= \{6, 8\}; & U \cup E &= U;\\ B \setminus E &= \{7, 8, 9\}; & E\setminus U &= \varnothing. \end{align*}\]

Example 1.24 (Relationships between sets) Consider the set $A$ defined using set-builder notation as: \[ A = \{ x \in \mathbb{R} \mid \sqrt{x^2 - 4} \in \mathbb{R}\}. \] This means that the set $A$ comprises the real elements $x$ such that the values of $\sqrt{x^2 - 4}$ are real numbers; that is, such that $x^2 - 4 \ge 0$. The values of $x$ can be defined as \[ A = \{ x \in\mathbb{R} \mid (-\infty, -2] \cup [2, \infty)\}; \] set $A$ contains real numbers less than or equal to $-2$, and real numbers greater than or equal to $2$.

Notice the use of the brackets: using the square brackets ‘$[$’ and ‘$]$’ is standard for showing that the indicated value is included in the interval, where as the round brackets ‘$($’ and ‘$)$’ is standard for showing that the indicated value is not included in the interval.

Example 1.25 (Set operations) We can define $\mathbb{N}_0 = \{ 0 \} \cup \mathbb{N}$.

We could write $\mathbb{Q} = \{\frac{m}{n}\mid m\in\mathbb{Z}, n \in \mathbb{Z}, n\ne 0\}$.

We can also write $\mathbb{Z} \in \mathbb{R}$, but $\mathbb{R} \notin \mathbb{Z}$.

Example 1.26 (Relationships between sets) Consider the set $A$ defined using set-builder notation as: \[ A = \{ x \in \mathbb{R} \mid \sqrt{x^2 - 4} \in \mathbb{R}\}. \] This means that the set $A$ comprises the real elements $x$ such that the values of $\sqrt{x^2 - 4}$ are real numbers; that is, such that $x^2 - 4 \ge 0$. This means that \[ A = \{ (-\infty, -2] \cup [2, \infty)\}; \] set $A$ contains real numbers less than or equal to $-2$, and real numbers greater than or equal to $2$.

Notice the use of the brackets: using the square brackets ‘$[$’ and ‘$]$’ is standard for showiing that the indicated value is included in the interval, where as the round brackets ‘$($’ and ‘$)$’ is standard for showing that the indicated value is not included in the interval.

Example 1.27 (Sets can be two-dimensional) Sets do not have to be one-dimensional. We could define the set $P$ as \[ P = \{(x, y)\in \mathbb{R}\times\mathbb{R} \mid (0 < x < 1)\cap(0 < y < 1) \}, \] where $\mathbb{R}\times\mathbb{R}$ means ‘the ordered pairs $(x, y)$ where both $x$ and $y$ are real numbers’. $P$ which defines a unit square on the Cartesian axes.

1.7 Set algebra

Set algebra has many rules; we only provide some. For sets $A$, $B$ and $C$ defined on the universal set $S$ these rules are defined.

The commutative laws are:

$A\cup B = B \cup A$
$A\cap B = B \cap A$.

The associative laws are:

$A\cup(B\cup C) = (A\cup B)\cup C$.
$A\cap(B\cap C) = (A\cap B)\cap C$.

The distributive laws are:

$A\cap (B\cup C) = (A\cap B)\cup (A \cap C)$.
$A\cup (B\cap C) = (A\cup B)\cap (A \cup C)$.

de Morgan’s law are:

$(A \cap B)^c = A^c \cup B^c$.
$(A \cup B)^c = A^c \cap B^c$.

The absorptions laws are:

$A\cup (A\cap B) = A$.
$A\cap (A\cup B) = A$.

The dominance laws:

$A\cup S = S$
$A\cap\varnothing = \varnothing$.

The idempotent laws:

$A\cup A = A$.
$A\cap A = A$.

Proof. We only give one example proof, for one of the commutative laws: prove $A\cup B = B \cup A$ (which may seem ‘obvious’).

To show this proposition, we need to show that \[\begin{align} (A \cup B) &\subseteq B\cup A\qquad\text{and \emph{also} that}\\ (B \cup A) &\subseteq A\cup B. \end{align}\] Consider the first statement, and consider an element $x$ such that $x\in (A\cup B)$. This means that either:

$x\in A$, in which case $x\in (B\cup A)$; or
$x\in B$, in which case $x\in (B\cup A)$.

In either case, $x \in (B\cup A)$ and so $(A\cup B)\subseteq B\cup A$.

The proof of the second statement is similar, and hence $A\cup B = B \cup A$.

These rules can be used to prove numerous other properties of sets.

Example 1.28 (Using set algebra) Consider the statement $A\cap (A^c \cup B)$. To simplify, set algebra rules can be used: \[\begin{align*} A\cap (A^c \cup B) &= (A\cap A^c) \cup (A\cap B)\qquad\text{(distributive law)}\\ &= \varnothing \cup (A\cap B)\qquad\text{(by definition of $A^c$)}\\ &= A\cap B.\qquad\text{(dominance law)} \end{align*}\] Thus, $A\cap (A^c \cup B) = A\cap B$.

1.8 Statistical computing with R

1.8.1 Using R

Computers and computer packages are essential tools in the application of statistics to real problems. In this book, the statistical package R is used, and will be used to illustrate various concepts to help you understand the theory (Sect. 2.11.3).

One way in which R can be used is to easily compute probabilities for specific distributions. Also, R can be used to verify (not prove) theoretical results obtained. To do this, a technique called computer simulation can be used.

Simulation can also be used to solve problems for which it may be difficult (or impossible) to obtain a theoretical result. Sometimes these numerical solutions to intractable analytical problems is termed Monte Carlo simulation.

We introduce R by showing how to operate with sets; more general information about using R is given in Sect. C. Greater functionality in working with sets is provided by installing and using the R package sets.

1.8.2 Simple example

Consider rolling a standard, fair six-sided die. Define $A$ as the set of numbers that can be rolled on the die, $B$ as the set of even numbers that can be rolled, and $C$ as the of numbers that can be rolled that are divisible by three.

This is a simple example, but R can be used to determine the elements in these sets, and the union and intersection of the sets.

First, we define the sets:

DieRolls <- 1:6 # Set A
RollsEven <- seq(2, 6, by = 2) # Set B
RollsDivisibleBy3 <- c(3, 6) # Set C
RollsEven # Set B
#> [1] 2 4 6
RollsDivisibleBy3 # Set C
#> [1] 3 6

Then use R to find the intersection and union:

intersect(RollsEven, RollsDivisibleBy3)
#> [1] 6
union(RollsEven, RollsDivisibleBy3)
#> [1] 2 4 6 3

The function setdiff() find the difference between two sets:

setdiff(RollsEven, RollsDivisibleBy3) # B \ C
#> [1] 2 4
setdiff(RollsDivisibleBy3, RollsEven) # C \ B
#> [1] 3

The function is.element() determines if a given element is contained in a given set:

is.element(RollsDivisibleBy3, RollsEven)
#> [1] FALSE  TRUE
is.element(RollsEven, RollsDivisibleBy3)
#> [1] FALSE FALSE  TRUE

1.8.3 More involved example

The above examples was simple enough to complete manually. However, the power of using computers is more obvious for more involved examples.

Consider the two sets: \[\begin{align*} A &= \{\text{Countries whose names have `a' as the \emph{second} letter}\};\\ B &= \{\text{Countries whose names end with `a'}\}. \end{align*}\]

In R, the names of the countries can be found by loading the countries package (assuming it is installed):

library("countries")

The list of country names are in the R vector list_countries():

head( list_countries() ) # Show the first five values only
#> [1] "Afghanistan"    "Åland Islands" 
#> [3] "Albania"        "Algeria"       
#> [5] "American Samoa" "Andorra"

First, we find the countries whose names have an a as the second letter (assuming it is always lower case); that is, we identify the elements in set $A$:

# Find where, in the list of countries, a country name has an `a` in position 2:
# (Assumes the letter is lower case)
Locate_a_Second <-  which( substr(list_countries(),
                                  start = 2, 
                                  stop = 2)
                           == "a")

# Now find the countries listed at those locations:
a_Second <- list_countries()[Locate_a_Second]

# How many countries are there whose names have an `a` as second letter?
length(a_Second)
#> [1] 57

Then, we find the countries whose names end with the letter a (assuming it is always lower case); that is, we identify the elements in set $B$. To do this, we first need to know how long the name of each country is:

# Find the length of the name of each country in the list:
Length_Country_Names <- nchar(list_countries()) # Length of each country name

Then we can proceed similar to having a as the second letter of the name:

# Find where, in the list of countries, a country name has an A in last position:
locate_Ends_With_a <- which( substr(list_countries(),
                                    start = Length_Country_Names,
                                    stop = Length_Country_Names)
                            == "a")

# Now find the countries listed at those locations:
Ends_With_a <- list_countries()[locate_Ends_With_a]

# How many countries are there whose names end with an `a`?
length(Ends_With_a)
#> [1] 79

Now we can find the countries whose names have an a as the second and as the last letters by finding the intersection between the two sets:

a_Second_And_Last <- intersect(a_Second, 
                               Ends_With_a)

# How many countries are there whose names have `a` as second and last letters?
length(a_Second_And_Last)
#> [1] 18

# What are these countries?
a_Second_And_Last
#>  [1] "Cambodia"                                    
#>  [2] "Canada"                                      
#>  [3] "Gambia"                                      
#>  [4] "Jamaica"                                     
#>  [5] "Latvia"                                      
#>  [6] "Malaysia"                                    
#>  [7] "Malta"                                       
#>  [8] "Mauritania"                                  
#>  [9] "Namibia"                                     
#> [10] "Panama"                                      
#> [11] "Papua New Guinea"                            
#> [12] "Saint Helena, Ascension and Tristan da Cunha"
#> [13] "Saint Lucia"                                 
#> [14] "Samoa"                                       
#> [15] "Saudi Arabia"                                
#> [16] "Wallis and Futuna"                           
#> [17] "Zambia"                                      
#> [18] "Taiwan, Province of China"

1.9 Exercises

Selected answers appear in Sect. E.1.

Exercise 1.1 Prove one of the idempotent laws in Sect. 1.7.

Exercise 1.2 Prove one of the dominance laws in Sect. 1.7.

Exercise 1.3 Consider the set of complex numbers $\mathbb{C}$ written in the form $a + bi$.

Use set-builder notation to define the set of complex numbers in terms of the set of real numbers $\mathbb{R}$.
Adapt your notation to define the set of purely imaginary numbers $\mathbb{I}$.

Exercise 1.4 Consider the real solutions to the general quadratic equation $y = ax^2 + bx + c = 0$ (where $a \ne 0$, since then the equation does not define a quadratic).

Using set-builder notation, define:

the universal set $U$, which defines all quadratics.
the set $R$ that contains all quadratics with two equal real roots.
the set $Z$ that contains all quadratics with no real roots.
the set $S$, in terms of $U$, $R$ and $z$, that contains all quadratics with exactly one real root.

Exercise 1.5 Consider the equation $y = \log(x^2 - 1)$ for real values of $y$. Using set-builder notation, define:

the set of values of $x$ for which $y$ has real values.
the set of values of $x$ for which $y > 1$.
the set of values of $x$ for which $y$ has the value zero.

Exercise 1.6 Define these sets: \[\begin{align*} S &= \{\clubsuit, \spadesuit\};\\ P &= \{ \text{Jack}, \text{Queen}, \text{King}, \text{Ace}\}\quad \text{(i.e., the picture cards)}, \end{align*}\] where $U$ is the universal set of all cards in a pack. Using set-builder notation, define:

the set $A$ that contains the black picture cards.
the set $B$ that contains the red picture cards.
the set $C$ that contains the red non-picture cards.

Exercise 1.7 In R, the names of all US states are contains in the built-in dataset state.name. Using this dataset, use R to:

find the set of US states who names begin with W.
find the set of US states who names begin with North.
find the set of US states who names end in a.
find the set of US states who names end in a, or start with W.
find the set of US states who names end in a, and start with W.
find the set of US states who names end in a, and do not start with W.

Exercise 1.8 In R, information about each US states in (mostly) 1977 is contained in the built-in dataset state.x77. Using this dataset, use R to:

find the set of US states whose average life expectancy exceeds $70$.
find the set of US states whose area is less than $500\,000$ square miles.
find the set of US states whose illiteracy rate is greater than $2$%.
find the set of US states whose percent of high-school graduates is less than $50$%.
find the set of US states whose illiteracy rate is greater than $2$%, and whose percent of high-school graduates is less than $50$%.
find the set of US states whose illiteracy rate is greater than $2$%, or whose percent of high-school graduates is less than $50$%.

(To view the help for this data, type ?state.x77 in R.)

Exercise 1.9 Using set-builder notation, define set $T$ as the values of $x$ for which $y = 1/x$ is a real value.

Exercise 1.10 Using set-builder notation, define set $L$ as the values of $x$ for which $y = \tan x$ is a real value.

Exercise 1.11 Explain what values are contained in set $G$, if it is defined as \[ G = \{ x\in\mathbb{R} \mid x^2 < 4\} \] What is the cardinality of set $G$?

Exercise 1.12 Explain what values are contained in set $B$, if it is defined as \[ B = \{x\in\mathbb{R} \mid \lfloor x \rfloor = x\}. \] In this expression, $\lfloor x \rfloor$ is the floor function, that rounds the value of $x$ to the next lowest integer (for example, $\lfloor \pi \rfloor = 3$).

What is the cardinality of set $B$?

Exercise 1.13 Use set algebra to show that $A\setminus(A\cap B) = A\cap B^c$.

Exercise 1.14 Use set algebra to show that $(A\setminus B)^c = A^c\cup B^c$.

Exercise 1.15 Use set algebra to show that $(A\cup B) \cap (A\cup B^c) \cap B = A\cap B$.

Exercise 1.16 Use set algebra to show that $(A\cap B) \cup (A\cap B^c) = A$.

Exercise 1.17 Suppose the set $C$ is defined as C = {H, T} the set of results from tossing a coin. Define the set $D$ that shows the results of two tosses of a coin, as an ordered pair. (See Example 1.27.)

Exercise 1.18 Define the following two sets: \[ S = \{\spadesuit, \clubsuit, \diamondsuit, \heartsuit\} \qquad\text{and}\qquad D = \{2, 3, 4, \dots, \text{Jack}, \text{Queen}, \text{King}, \text{Ace}\}. \] Use these two sets to define Set $C$ of ‘all cards in a standard pack’, as an ordered pair. (See Example 1.27.)

Preface

2 Probability